January 31, 2007
Quantization and Cohomology (Week 12)
Posted by John Baez
This week’s class on Quantization and Cohomology introduced the theme of ‘rigs’ (rings without negatives), foreshadowed last week:
-
Week 12 (Jan. 30) - Classical, quantum and statistical mechanics as ‘matrix mechanics’. In
quantum mechanics we use linear algebra over the ring ; in classical mechanics everything is formally the same, but we instead use the rig , where the addition is min and the multiplication is +. As a warmup for bringing statistical mechanics into the picture - and linear algebra over yet another rig - we recall how the dynamics of particles becomes the statics of strings after Wick rotation.
- Supplementary reading: Grigori L. Litvinov, The Maslov dequantization, idempotent and tropical mathematics: a very brief introduction. Also see the longer version here.
Last week’s notes are here; next week’s notes are here.
January 29, 2007
No Need to Apologise
Posted by David Corfield
Café regular John Armstrong has a blog. It goes by the name of The Unapologetic Mathematician. A subtle allusion to Hardy’s A Mathematician’s Apology, playing cleverly on the two meanings of apology?
CFT in Oberwolfach
Posted by Urs Schreiber
There will be an Arbeitsgemeinschaft (study group) in Oberwolfach, on Algebraic Structures in Conformal Field Theories, April 1 - April 7, 2007.
You can find the program and the application details here.
January 28, 2007
Another Interview
Posted by David Corfield
It’s worth taking a look at an interview Mikio Sato gave to Emmanuel Andronikof in 1990, published in February’s Notices of the American Mathematical Society. Sato is famous for algebraic analysis, D-modules, and the like, about which I know next to nothing. Perhaps if Urs continues to post on Geometric Langlands we’ll hear something about D-modules, as they appear to very relevant. You won’t learn much mathematics from the interview, but it gives a fascinating account of an indirect path to becoming one of the world’s leading mathematicians.
Concerning future directions, this passage caught my eye:
While methods of mathematical physics in quantum field theory have profited various branches of mathematics (topology, braid theory, number theory, geometry), the converse is not necessarily true. Today [remember this is 1990 - DC], mathematical physicists mostly use number theory or algebraic geometry. Mathematical physics is receptive only to higher developed areas of mathematics, some of which are exploited in superstring theory, though not to its full extent. Mathematics has not succeeded in providing a more effective way of computation than perturbation expansions. Of course, there are some primitive methods of computation, like the Monte-Carlo method. All these are kind of brute force computations, not refined mathematics, surely not refined enough for the problems physics is now confronted with, like determining the mass of particles or quarks. All these things are discussed on a very abstract level, not on a quantitative level. So I think that mathematical analysis should be developed much further to match the reality of physics.
Also see Pierre Schapira’s description of Sato’s work in the same edition of the Notices.
January 27, 2007
Peering Through the Veil
Posted by David Corfield
Twice in recent days I have confronted the possibility of experiencing a kind of alienation due to interviews. First, my co-author Darian Leader and I were interviewed by the New Scientist about our book Why Do People Get Ill?. A day or two later we got to see a draft of what was to be selected for publication. Space limitations have meant that statements attributed to one of us are composites of things said by either of us. I don’t think it matters much in terms of the information carried in the interview, but it feels strange to have sentences you never uttered marked as originating from you.
No such chopping in that other recent interview, the one Urs and John gave to Bruce Bartlett about this blog. Even hesitation and laughter have been carefully marked. Here the potential alienation arises from the possibility of being spoken about in a way which clashes with one’s self-image. Of course nothing like this happened, but I would like to take the opportunity to say something about John’s comment about me that when
he’s talking about the philosophy of mathematics, he’s very concerned about the sociology of mathematics, and how people interact, and how you can do mathematics well.
Now ‘sociology’ has a number of uses. On the one hand, it can be taken as a non-normative discipline which seeks to understand and describe how societies operate. Although there may be some or other philosophical stance operating behind the scenes, this activity would seem not to be philosophical as it stands. On the other hand, ‘sociology’ as applied to the study of science and mathematics, as in the ‘sociology of scientific knowledge’, tends to come with a strong dose of social constructivism, and a wish to unmask the resources and techniques of the powerful to represent the way things are. In this context the study of ‘norms’ is largely to understand how the powerful wield certain standards to maintain their position of prominence. We had a discussion about that stance starting back here.
January 26, 2007
Globular Extended QFT of the Charged n-Particle: String on BG
Posted by Urs Schreiber
To begin filling the definition of the charged quantum -particle with life, here I walk through a very simple but still interesting example: “a string on the classifying space of a 2-group ”.
This turns out to be a “globular extened quantum field theory” , which to a “point” of the shape assigns a 2-vector space of states namely the category of modules over the algebra of a certain groupoid – the loop groupoid of the 2-group – and which to a “string” of the shape assigns the 2-linear identity map on this 2-vector space
For the special case that the 2-group is the “string group of a compact, simple and simply connected Lie group” the 2-space of states over the point is the 2-space of -equivariant gerbe modules on , also known as certain D-branes on .
A (2-)state of the string on is a 2-linear 2-map which is nothing but a gerbe module/D-brane over , together with an automorphism
If we close the string by gluing its endpoints by means of a trace, we find that a state of the closed string is a function on connected components of
January 25, 2007
Classical vs Quantum Computation (Week 11)
Posted by John Baez
Today in our course on Classical vs Quantum Computation we covered lots of examples of 2-categories, to show how widespread these gadgets are:
-
Week 11 (Jan. 25) - Examples of 2-categories. The 2-category of categories. The fundamental 2-groupoid of a topological space. The 2-category of topological spaces, maps, and homotopies between maps. The 2-category of topological spaces, maps, and homotopies between maps. The 2-category implicit in extended topological quantum field theories, due to Jeffrey Morton. The 2-category implicit in string theory, due to Stolz and Teichner. Monoidal categories as one-object 2-categories. The 2-category of rings,
bimodules and bimodule homomorphisms. Monoidal categories as one-object 2-categories. The 2-category of rings, bimodules and bimodule homomorphisms.
Supplementary reading:- Jeffrey Morton, A double bicategory of cobordisms with corners.
- Stefan Stolz and Peter Teichner, What is an elliptic object? Section 4.2: the bicategory of conformal 0-, 1- and 2-manifolds.
Last week’s notes are here; next week’s notes are here.
January 24, 2007
Classical vs Quantum Computation (Week 10)
Posted by John Baez
This quarter in our course on Classical vs Quantum Computation, our goal is to repair a gaping hole in the usual application of category theory to computation — especially the lambda-calculus and its quantum generalizations. We want to be able to talk about the process of computation! For this, we need to get serious about 2-categories…
- Week 10 (Jan. 18) - Categorifying the concept of ‘category’ to get the concept of ‘2-category’ - in detail.
Last week’s notes are here; next week’s notes are here.
The Globular Extended QFT of the Charged n-Particle: Definition
Posted by Urs Schreiber
After thinking about it for a while (A B C D E F G H I J) it seems that I am finally at a point where I can venture to state a comprehensive formal definition of the structure whose working title was the charged quantum -particle.
The following definition is taken from the beginning of
The Globular Extended QFT of the String propagating on the Classifying Space of a strict 2-Group
which develops one of simplest interesting examples in more detail (to be discussed in a followup post).
The two definitions, discussed in detail below, roughly go like this:
Definition 1. A charged -particle is a setup internal to .
Definition 2. The quantization of a charged -particle is the -functor on obtained by pull-pushing through the correspondence
Cocycle Category
Posted by Urs Schreiber
Here is another guest post by Bruce Bartlett.
Luckily, Bruce is still at Fields in Toronto, attending the Thematic Program on Geometric Applications of Homotopy Theory.
Here he reports on something very interesting that is intimately related to our discussion of anafunctors.
Quantization and Cohomology (Week 11)
Posted by John Baez
-
Week 11 (Jan. 23) - Action as a functor from a category of “configurations” and “paths” to the real numbers (viewed as a one-object category). Three things physicists do with this functor: find its critical points, find its minima, and integrate its exponential. The analogy between the (classical) principle of least action and the (quantum) principle of path integration. The underlying analogy between the real numbers equipped the operations min and +, and the complex numbers with operations + and ×.
-
Supplementary reading: The Hamilton-Jacobi equation.
- Homework on another way to see Action as a functor.
- answers by Jeffrey Morton.
- answers by Toby Bartels.
- answers by Miguel Carrión Álvarez.
- answers by Derek Wise.
-
Supplementary reading: The Hamilton-Jacobi equation.
January 23, 2007
Two Café Owners Interviewed
Posted by David Corfield
As neither John nor Urs has announced it, readers might like to find out about their motivations for starting and running this blog in an interview they gave to Bruce Bartlett, available in written form and also as an MP3 file.
John commented:
I think all three of us - Urs, David and I - are pushing a new way of thinking: a very n-categorical way of thinking about a large bunch of ideas in math and physics. I’m very excited about this, because I can see how much potential it has. But we’re also simultaneously pushing a new idea of how to communicate ideas. And the combination is actually really, really interesting.
There’s an intriguing thought. If it weren’t n-categories which gripped us, would it make a difference to the way the blog works? Well, I can’t think of anything else which would allow us to talk about quantum gravity, logic and number theory in quite the same way. It seems to me at least as important a breakthrough as the burst of foundational activity in the decades around 1900.
Kenny Easwaran wrote:
It’s clear why other philosophers should care about notions of logic and basic arithmetic, and the possibility of knowledge of abstract objects. Maybe there’s reason for them to care about higher category theory, but I don’t think this has been made clear yet.
I answered that higher category theory showed that a prominent philosopher was wrong. I’m not sure what the rules are here. What else would I have to do, if this is not enough?
Higher Categories and Their Applications
Posted by John Baez
The Fields Institute workshop on n-categories was a lot of fun. If you couldn’t make it, you can still see what it was like. Here’s a webpage with abstracts, transparencies and photos of lots of the talks:
- Higher Categories and Their Applications, Fields Institute, January 9-13, 2007.
Someday soon I want to describe some of these talks — but not tonight.
January 21, 2007
Fusion and String Field Star Product
Posted by Urs Schreiber
From the point of view of functorial transport #, I describe the structure of the star product of string fields, and, as a special case, the fusion product of loop group representations.
Animals That Are Also Verbs
Posted by John Baez
This is just for fun — a bit like the puzzles I regularly post, but more open-ended.
I was walking over the bridge over the river Cam one day when it hit me: the verb ‘duck’ is related to the noun ‘duck’! Ducks hunt for food by ducking under the water! It shocked me that I’d never noticed the relation between these two words before. I wondered which came first: the animal or the verb. Did people call these birds ‘ducks’ because they duck under the water, or did they invent the verb ‘duck’ after watching what ducks do?
More generally: which other names of animals are also verbs?
January 19, 2007
More on Duality
Posted by David Corfield
Continuing our earlier discussion about duality, it’s worth noting a distinction that Lawvere and Rosebrugh introduce in chapter 7 of their Sets for Mathematics between ‘formal’ and ‘concrete’ duality. Formal duality concerns mere arrow reversal in the relevant diagrams, so
of course if the original diagrams had been given specific interpretation in terms of specific sets and mappings, such interpretation is lost when we pass to this formal dual in that the formal dualization process in itself does not determine specific sets and specific mappings that interpret the dualized statement. (p. 121)
Concrete duality, on the other hand, occurs in situations where a new diagram is formed from an old one by exponentiating each object with respect to a given dualizing object, e.g., becomes , with the dualizing object. The arrows are naturally reversed in the new diagram.
Now,
Not every statement will be taken into its formal dual by the process of dualizing with respect to , and indeed a large part of the study of mathematics
space vs. quantity
and of logic
theory vs. example
may be considered as the detailed study of the extent to which formal duality and concrete duality into a favorite correspond or fail to correspond. (p. 122)
Very relevant for concrete dualities is Peter Johnstone’s Stone Spaces, especially chapter 6 and its discussion of schizophrenic objects. For a hard-hitting review by Johnstone of some Universal algebraists’ attempt to treat duality while minimizing contact with category theory, see this.
Schizophrenic objects have found a role in clarifying -categorical issues. See Makkai and Zawadowski’s Duality for Simple -Categories and Disks.
Traces in Ottawa
Posted by John Baez
If you’re interested in logic, category theory, and diagrams, you’ll like this workshop:
- Recent advances in category theory and logic: applications of traces to algebra, analysis and categorical logic, April 28-30, 2007, University of Ottawa. Organized by Phil Scott, Rick Blute, and Pieter Hofstra.
What’s a trace, you ask? Read on…
Knot Homology in Faro
Posted by John Baez
This year’s Oporto Meeting on Geometry, Topology and Physics will actually take place in Faro, the capital of the Algarve — the southernmost region of Portugal:
- XVIth Oporto Meeting on Geometry, Topology and Physics, July 5-8 (2007), Faro, Portugal. Organized by Marco Mackaay, Roger Picken, Paulo Semi and others.
The subject this year will be The combinatorics, geometry, topology and physics of knot homology.
January 18, 2007
Multiplicative Intuitionistic Linear Logic
Posted by John Baez
The following guest post is by Mike Stay:
I’ve been trying to understand multiplicative intuitionistic linear logic (MILL) from a category-theoretic perspective, and I think I’ve figured out what’s going on — see below. As Richard Guy would say, this is “probably well-known to those who know it.” If you’re one of those, I’d appreciate any references you can think of.
Duality between Probability and Optimization
Posted by David Corfield
One of the reasons I have an interest in what we find out about mechanics in different rigs is that many machine learning algorithms are expressible in thermodynamic form, as the tutorial, Energy-Based Models: Structured Learning Beyond Likelihoods, by Yann LeCun made abundantly clear. We even see there the difference between working in the rig, where you keep the whole probabilistic apparatus, and the rig, where you just seek an optimal solution. The former typically takes greater effort to work with. Only in special situations is it analytically tractable, so one might use Monte Carlo techniques instead. On the other hand, in the probabilistic set-up the regularization term, which stops the inference problem being ill-posed, generally comes in the package for free, encoded in a prior.
Outside machine learning, there’s been much effort spent importing constructions into , so that you might hear of the Duality between Probability and Optimization. For a very good overview of the uses of semirings such as , Jonathan Golan’s Some Recent Applications of Semiring Theory is recommended. I never knew about Sammy Eilenberg or John Horton Conway’s role in their revival around 1970.
D-Branes from Tin Cans, III: Homs of Homs
Posted by Urs Schreiber
In D-Branes from Tin Cans, I: Arrow Theory of Disks I had started talking about the exercise of finding the right arrow theory for -disk holonomy - in the classical as well as in the quantized world.
For this is quite familiar:
Classically, we have a vector bundle with connection over a space . A path in is a 1-disk. Picking a section of over and over , respectively, i.e. morphisms and amounts to choosing a boundary insertion on the 1-disk.
The disk holonomy of the 1-disk under the transport of with boundary insertions and is the number
where denotes the parallel transport induced by .
There is a quantum version of this. After quantizing the above setup (for instance by pushing it forward to a point) we obtain a vector transport functor on the abstract worldline of the particle, which sends a worldline of length to a morphism in .
Now we can compute the “quantum 1-disk holonomy”. This is known as the (1-)disk correlator. If is a vector in the Hilbert space and is a covector in that space, then the quantum mechanical 1-disk correlator with and as “boundary insertions” looks like this: You may be more familar with this entity in the equivalent notation
The goal of the exercise now is to reformulate this situation arrow-theoretically in such a way, that
a) it is possible to blindly categorify it
b) and that blindly categorifying it yields all the structure we expect to see for 2-disk correlators of strings (= 2-particles), for 3-disk correlators of membranes (= 3-particles), and so on.
Since for higher this will involve lots of tin can diagrams

and since all information about the existence and the nature of D-branes is hopefully contained in these (unless that exercise remains unseccessful), the name of the game is building D-branes from tin cans. Obviously.
When I started doing this exercise, I noticed a curious fact: the arrow-theory for the 2-disk-correlator of the 2-particle looked almost exactly like the arrow-theory for the section of the 3-particle, living over the disk.
This was encouraging, because this relation between states of a 3-dimensional QFT and correlators of a 2-dimensional QFT is precisely one of the things whose better underdstanding motivates going through this exercise here in the first place.
But at that time I did not fully appreciate what was going on. Even though, with hindsight, I could have:
pairing an -section of an -transport functor with an -cosection involves the --functor, as described in the section 1.2 “A Rosetta Stone: arrow theory of quantum mechanics” in On 2D QFT - from Arrows to Disks. But the result of the pairing is itself an ()-transport functor. So we can take its sections, in turn, and pair them. The result is an -transport functors. And so on.
The general mechanism at work here is quite general and not restricted to the funny context that I am applying it to. I bet somewhere out there some category theorists have long ago thought about what I will briefly describe next:
Notes: -Fold Iterated -Pairings
January 17, 2007
Quantization and Cohomology (Week 10)
Posted by John Baez
I’m back in town and eager to continue lecturing about Quantization and Cohomology!
In last Fall’s lectures, we discussed the Lagrangian and Hamiltonian approaches to the classical mechanics of point particles, and sketched how these could be generalized to strings and higher-dimensional membranes by a process that we’ll ultimately see as categorification. This quarter we’ll start by bringing the quantum aspects of the theory into the game.
We begin with a review and a quick discussion of some basic but still incompletely understood questions:
-
Week 10 (Jan. 16) - A quick review of classical versus quantum mechanics, in both the Lagrangian and Hamiltonian approaches. What are path integrals, really? How do we quantize a classical Hamiltonian to obtain a quantum one?
- Supplementary reading: John Baez, Geometric quantization.
The notes from last class — the final class of the Winter quarter — are here. Next week’s notes are here.
January 16, 2007
Towards the FFRS Description of 2dCFT (A)
Posted by Urs Schreiber
With a small group of students here in Hamburg, we want to talk about stuff that will eventually enable us to understand the FFRS theorem, which explains how 2-dimensional rational conformal field theories are characterized by special Frobenius algebra objects internal to modular tensor categories.
I have no idea if we will really get to this point in finite time, or what else will happen. But at least tomorrow I shall, informally, begin by explaining some basics of 2-dimensional topological field theory and its description in terms of Frobenius algebras.
Here are handwritten notes for the first session:
It is clear that this leaves a lot of room for improvement. But it is a start.
Aaronson on the Nature of Quantum Mechanics
Posted by Urs Schreiber
Scott Aaronson is a remarkable thinker and expositor, as you can convince yourself of for instance by following his blog.
He is among the few who managed to pull off something of genuine intellectual interest from a meme that is currently haunting the high energy physics community, known as the “anthropic principle”.
If you want to see a lot of confusion among smart people, google for the “anthropic principle”. Then go back and read this piece by Scott Aaronson to see the difference.
And if you happen to have followed the stringy part of the blogosphere in the last months and are in need of some great entertainment, you should not miss the blog entry accompanying this.
But I am writing this here not to talk about the anthropic principle, but about quantum mechanics.
On this blog here, we enjoy, from time to time, to muse about the nature of quantum mechanics in the light of general abstract nonsense. Lately for instance in the entry Common Applications and also in the discussion starting here.
Scott Aaronson is a complexity theorist, thinking about quantum computation. Accordingly, he has his views on the nature of quantum mechanics. In his latest transcript of a lecture he is giving, he explains to his students why there are various reasons that we should not be surprised about the nature of quantum mechanics. An intellectual treat. Even - and maybe especially - for the layman.
In essence, he explains that if we are going to consider any generalization of ordinary classical probability theory, then quantum probability is the most natural of all alternatives.
Personally, I believe that if we are ever going to really understand “Why quantum mechanics?”, it will involve considerations considerably beyond what Scott Aaronson mentions there, namely such more along the lines of John’s Quantum Quandaries. But he certainly mentions some noteworthy points.
Among them, somewhat vague but intriguing, is a relation to Fermat’s last theorem that he points out.
But the most powerful insight he mentions is probably that nonlinear deformations of quantum mechanics would allow to solve NP problems in polynomial time.
In order to appreciate this, you may want to read Aaronson’s Reasons to Believe.
P.S.
John mentioned many related things in TWF 235.
January 14, 2007
Khovanov Homology
Posted by Urs Schreiber
The workshop is over and finally there is some time to let all that information sink in.
One thing I wanted to learn, and which I learned now, are some basic ideas of Khovanov homology.
On my flight to Canada I looked at
Dror Bar-Natan
Khovanov’s Homology for Tangles and Cobordisms
and
Aaron D. Lauda, Hendryk Pfeiffer
Open-closed TQFTs extend Khovanov homology from links to tangles
math.GT/0606331.
This morning Aaron gave a nice talk on this work. I am far from having absorbed everything, but here are some notes.
January 13, 2007
The First Part of the Story of Quantizing by Pushing to a Point…
Posted by Urs Schreiber
…in which the author entertains himself by computing the space of states of a charged particle by pushing its parallel transport forward to a point. Just for fun.
January 11, 2007
Ubiquitous Duality
Posted by David Corfield
I’m in one of those phases where everywhere I look I see the same thing. It’s Fourier duality and its cousins, a family which crops up here with amazing regularity. Back in August, John wrote:
So, amazingly enough, Fourier duality and the duality between syntax and semantics for algebraic theories are part of the same family of ideas.
With more work one could find a common generalization and prove a theorem which had both of these results as a special case. I don’t know if anyone has done this yet. If not, they should!
and told us something about Tannaka-Krein duality. (A good opportunity there for a contribution to Wikipedia.)
We had Urs telling us about Geometric Langlands as involving a form of categorified Fourier transform, which suggests that perhaps the whole Langlands program may likewise.
Then I quoted Michael Atiyah:
This replaces a space by its dual space, and in linear theories that duality is just the Fourier transform. But in non-linear theories, how to replace a Fourier transform is one of the big challenges. Large parts of mathematics are concerned with how to generalise dualities in nonlinear situations. Physicists seem to be able to do so in a remarkable way in their string theories and in M-theory…understanding those non-linear dualities does seem to be one of the big challenges of the next century as well.
We also have spoken about the Laplace transform as a twin of the Fourier transform, and their idempotent cousin the Legendre transform.
Elsewhere, I heard it said that work on arithmetic progressions of primes, by Tim Gowers and others, had something to do with a ‘quadratic’ Fourier analysis, mentioned in the May 18 entry here.
There must be some common framework, as John remarked. How much power does Brian Day’s construction pack?
January 8, 2007
Universality in Particularity
Posted by David Corfield
To keep me from brooding on the pleasure I’m missing out on by not being with my Café co-hosts in Toronto, let me try out a blog post.
In just about every academic endeavour to which I’ve applied myself, I have run up against the problem of striking the right balance between specificity and generality. When you’re looking to capture some complex entity and there are many possible instances to choose from, should you opt for a few highly detailed case studies, or are you better off selecting a few aspects of a multitude of examples, perhaps to submit them to statistical analysis?
Take the entity ‘episode of mathematical reasoning’. Should one take as central what is common to all such reasoning, or should one devote many pages to a detailed account of a handful of case studies? Differences of opinion on this score as regards science have occurred frequently in the philosophy of science, and in philosophically-minded history of science. In Image and Logic, Peter Galison criticises Kuhn for imagining that there might be a structure to scientific revolutions. He likens this to seeking to understand the structure of European civilisations by a case study of France. On the other hand, many analytic philosophers would find Kuhn far too interested in the specificity of historical cases, and seek some universal insight into inductive reasoning.
January 5, 2007
Classical vs Quantum Computation (Week 9)
Posted by John Baez
Here are the first of the Winter quarter notes on Classical versus Quantum Computation. This quarter we’ll start categorifying everything we did last time!
- Week 9 (Jan. 4) - Brief review of categories and computation: objects as data types, morphisms as equivalence classes of programs. Why we must categorify our work so far to see computation as a process. The strategy of categorification. Categorifying the concept of ‘monoid’ to get the concept of ‘monoidal category’. Categorifying the concept of ‘category’ to get the concept of ‘(weak) 2-category’ (also known as ‘bicategory’).
Last week’s notes are here.
January 4, 2007
FFRS on Uniqueness of CFT: Sewing as Natural Transformation
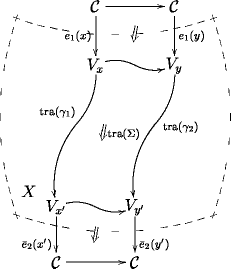
Posted by Urs Schreiber
A comment on “sewing” in 2-dimensional quantum field theory, and on its description in terms of natural transformations as used in the recent FFRS paper discussed here.
January 3, 2007
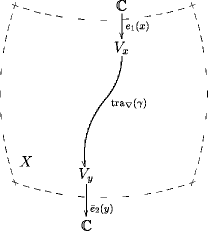
FFRS on Uniqueness of CFT: Morphisms into Transport Functors
Posted by Urs Schreiber
One of the reformulations of aspects of the FFRS framework which I just mentioned concerns the observation that a solution to the “sewing constraints” of 2d CFT (essentially: “sewing” = “functoriality”) can be regarded as a natural transformation from a trivial TFT functor to a nontrivial one.
FFRS on Uniqueness of Conformal Field Theory
Posted by Urs Schreiber
J. Fjelstad, J. Fuchs, I. Runkel, Ch. Schweigert
Uniqueness of open/closed rational CFT with given algebra of open states
hep-th/0612306
 Posts with this logo use
Posts with this logo use