August 31, 2008
This Week’s Finds in Mathematical Physics (Week 269)
Posted by John Baez
In week269 of This Week’s Finds, see more of Jupiter’s moon Io:

Then learn about honeycombs, the work of Kelvin, the Weaire-Phelan structure, and gas clathrates.
August 30, 2008
Imperfections, Ambiguities and Physics
Posted by David Corfield
I mentioned Lautman’s association of, on the one hand, Descartes’ argument to the existence of a perfect being (God) from an awareness of his own imperfections with, on the other, a mathematical argument to the existence of an algebraically closed field from the inability to factor polynomials in a given field, or to the existence of a simply connected space from the inability to contract all loops in a given space.
This perfection/imperfection ‘dialectic’ involves our realising from an imperfect state that there is a perfect state, and also from the nature of the imperfections what are the attributes of the perfect state.
Now does this thought have any resonance in physics? Are there specifically physical manifestations of this phenomenon? Or to the extent that we find these, such as Doron Gepner’s Galois Groups in Rational Conformal Field Theory, should we say that everything Galoisian ‘factors’ through the mathematics?
On the other hand, if we wanted a natural language description of the mathematical phenomena, is the perfection/imperfection pairing the best way, or is Galois’ own ambiguity theory not more accurate? In which case, although ambiguity might be thought an imperfection, the commonality with the cartesian situation is lessened.
Finally, are physical manifestations better described as ambiguities rather than imperfections? Don’t I remember something on ‘defects’ in nematic crystals in one of those mathematics of gauge theory textbooks? Ah yes, Topology and Geometry for Physicists. So, does the existence of a crystal defect tell us about a perfected crystal, even if physically unrealisable? Similarly, how could we describe the Aharonov-Bohm effect?
August 29, 2008
New Structures for Physics I
Posted by John Baez
guest post by Bob Coecke
Following John’s great idea for having a public review here at the café of his and Mike Stay’s chapter for the New Structures for Physics volume(s) which I am editing, which happened here and here, John had the even better idea to have several chapters for these volumes reviewed here at the café.
I will submit them in pairs as guest posts. The ones we start with are two papers which, together with John and Mike’s, make up an ABC on category theory and monoidal categories and categorical logic in particular.
August 22, 2008
Henri Cartan, July 8, 1904 - August 13, 2008
Posted by John Baez
At the age of 104, Henri Cartan died last Wednesday. His father was Élie Cartan. He was one of the founding members of the Bourbaki group in 1935. Starting around 1945, the famous Séminaire Henri Cartan in Paris covered topics in several complex variables, sheaf theory, spectral sequences and homological algebra in a way that greatly influenced Jean-Pierre Serre, Armand Borel, Alexander Grothendieck, Frank Adams, and others. In 1956, he coauthored the magnificent book Homological Algebra with Samuel Eilenberg. His students include Douady, Godement, Karoubi, Serre and Thom. Truly a giant!
Melliès on Functorial Boxes
Posted by David Corfield
John once mentioned the slides of Paul-André Melliès’s talk Functorial boxes in string diagrams. Now you can read a 44 page tutorial on this topic.
I’m a little confused as I noted back then that I saw a resemblance between Peirce’s ‘cuts’ or ‘seps’ for negation and Melliès’s treatment of negation from page 80 of the slides onwards. However, the slides end at p. 78, and there is no mention of negation in the tutorial.
Anyway, in view of the fact that negation may be construed as a monoidal functor, perhaps Peirce had an amazingly astute premonition of things to come.
How interesting! I’ve just seen that Fernando Zalamea (mentioned in this post as a fellow admirer of Lautman) has a paper Towards a Complex Variable Interpretation of Peirce’s Existential Graphs. I’ll just go and read that over a coffee.
August 21, 2008
The Weaire–Phelan Structure
Posted by John Baez
“Oh no!” you think, reading the title of this post. “Yet another obscure mathematical structure! I’m still struggling with Polish spaces, Hilsum–Skandalis maps, and Fell bundles. Sometimes I wish those bloggers at the -Café would just shut up and let me think.”
You’ll be relieved, perhaps, that the Weaire–Phelan structure is something you can actually see. In fact, it was chosen as the design for the National Aquatics Center for the 2008 Olympics — a building also known as the ‘Water Cube’:

Homotopical Algebra with Applications to Mathematical Physics
Posted by Urs Schreiber
guest post by Jim Stasheff
We are organizing a special session at the 2009 Spring Southeastern Section Meeting in Raleigh, NC, during April 4-5, 2009:
Session Title: Homotopical Algebra with Applications to Mathematical Physics
Organizers:
Tom Lada, North Carolina State University, lada at math.ncsu.edu (Main Contact)
Jim Stasheff, UNC Chapel Hill, Emeritus, jds at math.upenn.edu
Various aspects of homotopy algebras such as , , and open-closed homotopy algebras are currently the object of research by a large number of mathematicians. These algebras are closely linked to a variety of topics in mathematical physics, for example, open string theory, closed string theory, gauge theory. This session will provide a forum for reports on current developments in both areas – algebraic structures as well as physical implications.
We particularly encourage graduate students to report on their current research on these topics. We hope to have at least one lecture that will present the overall picture that relates these subjects. If you are interested in giving such a survey, please let us know.
If you are interested, even provisionally, please respond to both of us. The official deadline for submitting an abstract to the AMS is —.
Polish Spaces
Posted by John Baez
Point-set topology has a bit of a dry reputation. I guess this is because a lot is known about it, and people who need it can usually find what they want in textbooks. But it keeps coming up…
For example, Yetter’s paper on infinite-dimensional categorified Hilbert spaces has forced me to learn about Polish spaces. A Polish space is a topological space that’s homeomorphic to a separable complete metric space.
And now I’m dying to know the answer to this:
Is every second-countable locally compact Hausdorff space a Polish space?
Can you help? I have some evidence that the answer is yes, but I don’t completely trust it.
Freed on Chern-Simons
Posted by David Corfield
After all these years there’s a pleasing amount I can understand of Daniel Freed’s very interesting Remarks on Chern-Simons Theory, dedicated to MSRI on its birthday. Something I don’t remember ever being discussed is the need to “integrate the scale-dependent and scale-independent aspects” of quantum field theory, as Freed does from p. 26 onwards.
Before this, concerning categorification, he tells us
…an category has category number , a set has category number , and an element in a set has category number . It is a feature of many parts of geometry over the past 25 years that the category number of objects and theorems has increased. Whereas theorems about equivalence classes–sets–used to be sufficient, new questions demand that automorphisms be accounted for: whence categories. This trend has affected–some would say infected–parts of quantum field theory as well. (p. 17)
I must find a student to work on metaphors of diseases applied to pieces of mathematics –e.g., Gruppenpest, q-disease (any others?). We might imagine such metaphors being used to deplore, perhaps ironically, a turn taken by a field. There’s a hint of some negative sentiment in Freed’s paper.
I once joked that every mathematician also has a category number, defined as the largest integer such that (s)he can think hard about -categories for a half-hour without contracting a migraine. When I first said that my own category number was one, and in the intervening years it has remained steadfastly constant whereas that of many around me has climbed precipitously, if not suspiciously.
Of course, the concern could be more that some people are climbing the ladder too rapidly for their own good, even while admitting that the ladder should be climbed.
August 20, 2008
Elvis Zap does the Calculus Rap
Posted by John Baez
The disturbing trend of math professors making silly rap videos seems to be spreading:
- Professor Elvis Zap, A capella calculus rap.
Lucky for him, this guy already has tenure. Here in California, even kids do slicker math raps:
- Franklin Gervaccio, Show me a sine.
August 19, 2008
Spivak on Derived Manifolds
Posted by John Baez
Derived categories are an efficient way to “infinitely categorify” a given concept without even needing to know about -categories. They don’t do everything! But, they let you go quite far without a vast amount of effort — especially since lot of technology has been developed over the years that you can simply grab off the shelf and use.
For example, the derived category of abelian groups is not a full-fledged approach to dealing with ‘weak abelian -groups’: for those you need infinite loop spaces, or in other words, connective spectra. But, there’s a very precise sense in which derived category of abelian groups is a way of handling strict abelian -groups and weak maps between these. And that’s pretty good.
So, it’s no surprise that derived categories — and their nonabelian brethren, model categories — are taking over the mathematical universe. And once these get the foot in the door, more general infinitely categorified concepts are sure to follow. For example, we’ve recently seen the rise of derived algebraic geometry, where spectra take the place of abelian groups, and ring spectra take the place of commutative rings:
- Bertrand Toen and Gabriele Vezzosi, Algebraic geometry over model categories (a general approach to derived algebraic geometry).
-
Jacob Lurie, Derived algebraic geometry:
I: Stable -categories.
II: Noncommutative algebra .
III: Commutative algebra .
IV: Deformation theory.
It would be a full-time job just keeping up with this subject.
But now we’re seeing the next phase: derived differential geometry!
August 17, 2008
Bergman on Infinity-Vector Bundles Coupled to Topological Strings
Posted by Urs Schreiber
As Aaron Bergman kindly pointed out here, he has an interesting article
Aaron Bergman
New Boundaries for the B-Model
arXiv:0808.0168
which gives a direct interpretation of the derived categories of coherent sheaves appearing in topological strings in terms of connections on -(Chan-Paton)-vector bundles, using a crucial insight by Jonathan Block.
Formerly, the way to see that the branes (= boundary conditions) of the topological B-model string are objects in a derived category of coherent sheaves was somewhat involved and a bit mysterious. Once upon a time I had tried to summarize the main steps involved as reviewed by Aspinwall here
Now, Jonathan Block showed that these derived categories of coherent sheaves are actually equivalent to homotpy categories of representations of holomorphic tangent Lie algebroids on chain complexes – but these are special cases of flat linear (as opposed to principal) -connections.
Aaron Bergman takes this theorem at face value and concludes that therefore it should be true that there is a direct way to see that the boundary conditions of the topological B-string come from such flat -vector bundles with connection, pretty much analogous to how an ordinary conformal string (the “physical string”) couples on D-branes to ordinary (maybe -graded) vector bundles with connection.
As an ansatz, he considers boundary insertions in the path integral that should correspond to the generalization of the familiar holonomy along the String’s boundary of the pulled back connection to the setup. He derives that this satisfies the B-string’s topological invariance precisely if the flat -connection satisfies the appropriate axioms it should satisfy. He then derives that, similarly, imposing the required topological invariance on the boundary field insertions interpolating between two such flat -connections yields the right notion of morphism in the category of flat -connections that Jonathan Block considered.
Differential Graded Clifford Algebra
Posted by Urs Schreiber
Take graded Grassmann algebras and equip them with a differential of degree +1 squaring to 0. The result, quasi-free differential graded algebras, happens to be equivalent to -Lie algebras whose bracket -functor is strictly skew symmetric but satisfies the Jacobi identity only up to higher coherent equivalence.
What natural generalizations of this are available such that skew symmetry is relaxed? There is an obvious one: Grassmann algebra generalizes to Clifford algebra if skew-symmetry is relaxed, the failure of skew symmetry being measured by a bilinear symmetric form.
I had suggested that we should generalize everything we are doing with quasi-free differential graded-commutative algebras to differential graded Clifford algebras.
For instance the “differential homotopy hypothesis” which relates spaces to DGCAs by sending a space to the DGCA of forms on and sends a DGCA to the classifying space of flat -valued differential forms would be generalized to a “Riemannian homotopy hypothesis” where a Riemannian space is sent to the graded Clifford algebra of sections of the deRham spinor bundle with differential given by the Dirac operator. On the other side we’d consider generalizations of the familiar Chevalley-Eilenberg and Weil DGCAs of -algebras to deformations where graded symmetric bilinear forms deform the graded-symmetric wedge products to a graded Clifford product.
Now, as Hisham Sati kindly points out to me, aspects of the latter have already been considered in the literature before. For an ordinary Lie algebra with non-degenarate bilinear invariant form , the article
A. Alekseev and E. Meinrenken
The non-commutative Weil algebra
arXiv:math/9903052
considers the deformation of the Chevalley-Eilenberg algebra from a differential graded commutative algebra to a differential graded Clifford algebra with the Clifford product controled by . Notice that the same kind of bilinear invariant forms control Dmitry Roytenberg’s weak Lie 2-algebras. And notice that due to the grading this amounts to regarding the Clifford pairing to be of degree -2 (sending two degree 1 generators to a scalar in degree 0).
On top of that, this article deforms also the corresponding Weil algebra (well, in fact the authors do not consider the CE-algebra separately, I just do this here to amplify the pattern). Now, in that the shifted copy of appears in degree 2 and hence a degree -2 Clifford structure here is an skew bracket. The natural such bracket in the game is the original Lie bracket, so they take the shifted part of the Weil algebra to be the universal enveloping algebra of .
The resulting structure is not unrelated to what happens in BV-formalism with the introduction of the anti-fields: the ordinary differential on the Weil algebra still is a differential on its Clifford-deformation, but there now it is “Hamiltonian” in the sense that its action is given by a graded commutator with an element of the algebra – that element is a kind of Dirac operator. Its square is the quadratic Casimir operator.
Lots of nice things to be explored here. But I’ll leave it at that for the moment.
August 15, 2008
Connections on Nonabelian Gerbes and their Holonomy
Posted by Urs Schreiber
Finally this sees the light of day:
U.S. and Konrad Waldorf
Connections on non-abelian Gerbes and their Holonomy
arXiv:0808.1923
Abstract: We introduce transport 2-functors as a new way to describe connections on gerbes with arbitrary strict structure 2-groups. On the one hand, transport 2-functors provide a manifest notion of parallel transport and holonomy along surfaces. On the other hand, they have a concrete local description in terms of differential forms and smooth functions.
We prove that Breen-Messing gerbes, abelian and non-abelian bundles gerbes with connection, as well as further concepts arise as particular cases of transport 2-functors for appropriate choices of structure 2-group. Via such identifications transport 2-functors induce well-defined notions of parallel transport and holonomy for all these gerbes. For abelian bundle gerbes with connection, this induced holonomy coincides with the existing definition. In all other cases, finding an appropriate definition of holonomy is an interesting open problem to which our induced notion offers a systematical solution.
August 14, 2008
Lautman on Reciprocity
Posted by David Corfield
In ‘Nouvelles Recherches sur la Structure Dialectique des Mathématiques’ (1939), Albert Lautman discusses the use of analysis in number theory. He notes that some have felt uncomfortable with this use and have sought to eliminate it. But Lautman sees no metaphysical necessity for this ‘purification’. Rather than take arithmetic as metaphysically prior to analysis, instead he proposes that we consider them equally as realisations of the same ‘dialectical’ structures.
He gives the example of reciprocal entities. In arithmetic we have quadratic reciprocity, where the Legendre symbols are acting as a kind of inverse to each other.
He goes on to note that it has been possible to generalise reciprocity in two different ways. First, to algebraic integers in any field. Second, to allow more general congruences, not just to a square, but to other powers. This has been achieved algebraically he notes, but he adds that Hecke has also provided analytic means of deriving general quadratic reciprocity results using theta functions.
Here we define
noting that singular points are at , a rational, but that for any such , takes a finite value. Then we have
This reciprocity, he claims, is the mainspring of the transcendental proof of quadratic reciprocity. The same dialectical idea is manifesting itself in different branches. He continues
This dialectical idea of reciprocity between elements can be so clearly distinguished from its realisations in arithmetic and in in analysis that it is possible to find a certain number of other mathematical theories in which it realises itself similarly.
He then claims that the dimensions and in Poincaré duality associated to a manifold of dimension also stand similarly in an inverse relationship, and further that Weil has shown (1937) a relationship between reciprocity laws and duality theorems.
Do people recognise a useful thought here? Is there a ‘walking’ reciprocity realising itself in different situations?
Bimodules Versus Spans
Posted by John Baez
Bimodules and spans show up a lot in applications of category theory to physics, perhaps because they get along with the ‘reversibility’ we have come to expect. Given an -bimodule, we can think of it as a morphism from the ring to the ring , and we can ‘compose’ these morphisms by tensoring them… but we can also turn them around: any -bimodule can be thought of as an -bimodule, and when our rings are commutative we don’t even need to bother with that ‘op’. Similarly, we can compose spans of sets but also turn them around.
I always thought bimodules and spans should be related, but only recently did I learn exactly how, thanks to Paul-André Melliès. The relation so nice I’ll present it as a series of puzzles. If these puzzles are too easy for you, please let others take a try first.
August 6, 2008
This Week’s Finds in Mathematical Physics (Week 268)
Posted by John Baez
In week268 of This Week’s Finds see a stunning view of Jupiter’s moon Io, and then learn about Frobenius algebras in physics and logic…
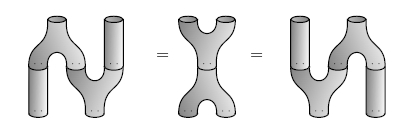
… and a bit about modular tensor categories and music theory, too!
Visiting Grothendieck
Posted by John Baez
Some people try to climb Mt. Everest or find an ivory-billed woodpecker; others attempt to track down the mysterious Alexander Grothendieck, who left home in 1991 and never came back. It’s probably not a wise thing to do. But surely someone is bound to try! After all, when perhaps the most visionary mathematician of the century simply goes and disappears, people are left with many questions.
Michael Barr pointed this out on the category theory mailing list:
- Roy Lisker, Visiting Alexandre Grothendieck.
Here’s a quote, just to get you interested…
August 2, 2008
Categorified Symplectic Geometry and the Classical String
Posted by John Baez
After weeks of polishing, maybe this is ready for the arXiv:
- John Baez, Alex Hoffnung and Chris Rogers, Categorified symplectic geometry and the classical string.
We’ve already talked about this paper. Besides the title, what’s new?
 Posts with this logo use
Posts with this logo use 














