August 28, 2017
Schröder Paths and Reverse Bessel Polynomials
Posted by Simon Willerton
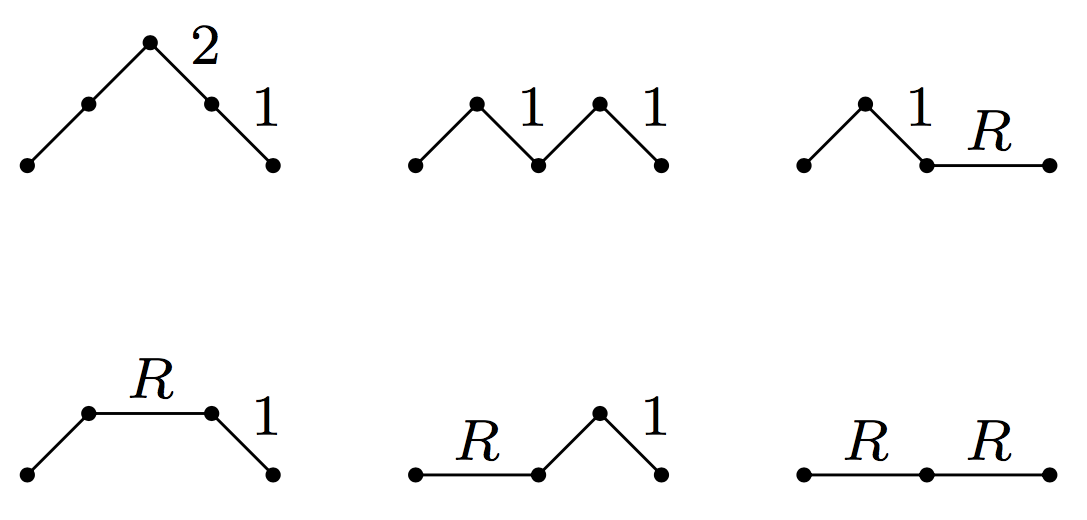
I want to show you a combinatorial interpretation of the reverse Bessel polynomials which I learnt from Alan Sokal. The sequence of reverse Bessel polynomials begins as follows.
To give you a flavour of the combinatorial interpretation we will prove, you can see that the second reverse Bessel polynomial can be read off the following set of ‘weighted Schröder paths’: multiply the weights together on each path and add up the resulting monomials.
In this post I’ll explain how to prove the general result, using a certain result about weighted Dyck paths that I’ll also prove. At the end I’ll leave some further questions for the budding enumerative combinatorialists amongst you.
These reverse Bessel polynomials have their origins in the theory of Bessel functions, but which I’ve encountered in the theory of magnitude, and they are key to a formula I give for the magnitude of an odd dimensional ball which I have just posted on the arxiv.
In that paper I use the combinatorial expression for these Bessel polynomials to prove facts about the magnitude.
Here, to simplify things slightly, I have used the standard reverse Bessel polynomials whereas in my paper I use a minor variant (see below).
I should add that a very similar expression can be given for the ordinary, unreversed Bessel polynomials; you just need a minor modification to the way the weights on the Schröder paths are defined. I will leave that as an exercise.
August 27, 2017
A Puzzle on Multi-Sorted Lawvere Theories
Posted by John Baez
I hope you know that a Lawvere theory is a category with finite products where the objects are all of the form for some object . A model of is a finite-product-preserving functor . There’s a category where the objects are models and the morphisms are natural transformations between such functors. Many familiar algebraic structures defined by -ary operations and equations, like groups or vector spaces over some field , can be seen as models of Lawvere theories. So, there’s a Lawvere theory for which is equivalent to , another one that gives , and so on.
Categories of this sort have been studied a lot and are sometimes called finitary monadic categories or finitary algebraic categories (though sometimes the latter term is used more generally — see the link). These categories always have coproducts, so it’s natural to wonder when the canonical morphism
is monic. After all, it’s true in and , and in enough other cases that people sometimes call the ‘inclusion’ of an object in .
But is not always monic in the category of models of a Lawvere theory. Can you think of a counterexample before read on?
August 19, 2017
Simplicial Sets vs. Simplicial Complexes
Posted by John Baez
I’m looking for a reference. Homotopy theorists love simplicial sets; certain other topologists love simplicial complexes; they are related in various ways, and I’m interested in one such relation.
Let me explain…
August 11, 2017
Magnitude Homology in Sapporo
Posted by Tom Leinster
John and I are currently enjoying Applied Algebraic Topology 2017 in the city of Sapporo, on the northern Japanese island of Hokkaido.
I spoke about magnitude homology of metric spaces. A central concept in applied topology is persistent homology, which is also a homology theory of metric spaces. But magnitude homology is different.
It was brought into being one year ago on this very blog, principally by Mike Shulman, though Richard Hepworth and Simon Willerton had worked out a special case before. You can read a long post of mine about it from a year ago, which in turn refers back to a very long comments thread of an earlier post.
But for a short account, try my talk slides. They introduce both magnitude itself (including some exciting new developments) and magnitude homology. Both are defined in the wide generality of enriched categories, but I concentrated on the case of metric spaces.
Of course, John’s favourite slide was the one shown.
A Graphical Calculus for Proarrow Equipments
Posted by John Baez
guest post by David Myers
Proarrow equipments (which also go by the names “fibrant double categories” and “framed bicategories”) are wonderful and fundamental category-like objects. If categories are the abstract algebras of functions, then equipments are the abstract algebras of functions and relations. They are a fantastic setting to do formal category theory, which you can learn about in Mike’s post about them on this blog!
For my undergraduate thesis, I came up with a graphical calculus for working with equipments. I wasn’t the first to come up with it (if you’re familiar with both string diagrams and equipments, it’s basically the only sort of thing that you’d try), but I did prove it sound using a proof similar to Joyal and Street’s proof of the soundness of the graphical calculus for monoidal categories. You can see the full paper on the arXiv, or see the slides from a talk I gave about it at CT2017 here. Below the fold, I’ll show you the diagrams and a bit of what you can do with them.
August 5, 2017
Instantaneous Dimension of Finite Metric Spaces via Magnitude and Spread
Posted by Simon Willerton
In June I went to the following conference.
This was held at the Będlewo Conference Centre which is run by the Polish Academy of Sciences’ Institute of Mathematics. Like Oberwolfach it is kind of in the middle of nowhere, being about half an hour’s bus ride from Poznan. (As our excursion guide told us, Poznan is 300km from anywhere: 300 km from Warsaw, 300 km from Berlin, 300 km from the sea and 300 km from the mountains.) You get to eat and drink in the palace pictured below; the seminar rooms and accommodation are in a somewhat less grand building out of shot of the photo.
I gave a 20-minute long, magnitude-related talk. You can download the slides below. Do try the BuzzFeed-like quiz at the end. How many of the ten spaces can just identify just from their dimension profile?
To watch the animation I think that you will have to use acrobat reader. If you don’t want to use that then there’s a movie-free version.
The Rise and Spread of Algebraic Topology
Posted by John Baez
People have been using algebraic topology in data analysis these days, so we’re starting to see conferences like this:
- Applied Algebraic Topology 2017, August 8-12, 2017, Hokkaido University, Sapporo, Japan.
I’m giving the first talk at this one. I’ve done a lot of work on applied category theory, but only a bit on on applied algebraic topology. It was tempting to smuggle in some categories, operads and props under the guise of algebraic topology. But I decided it would be more useful, as a kind of prelude to the conference, to say a bit about the overall history of algebraic topology, and its inner logic: how it was inevitably driven to categories, and then 2-categories, and then -categories.
This may be the least ‘applied’ of all the talks at this conference, but I’m hoping it will at least trigger some interesting thoughts. We don’t want the ‘applied’ folks to forget the grand view that algebraic topology has to offer!
 Posts with this logo use
Posts with this logo use