November 30, 2009
Feferman Set Theory
Posted by Mike Shulman
There’s been a bunch of discussion online recently (e.g. SBS, MathOverflow 1, 2, 3, etc.) about set-theoretic foundations for category theory, the role of universes, and so on. So I thought I would take this opportunity to advertise a set theory which isn’t that well-known, but which I find particularly pleasing as a foundation for category theory. I’ll call it strong Feferman set theory, since it is a stronger variant of a theory proposed by Solomon Feferman in his paper “Set-theoretical foundations of category theory.” Feferman called his theory ZFC/S (“ZFC with smallness”), and thus strong Feferman set theory could reasonably be called “ZMC/S,” for reasons explained below. (Feferman called the strong variant “ZFC/S + RIn(S)”.)
November 27, 2009
Dold–Kan Question
Posted by John Baez
Lately I’ve been writing a whole bunch of issues of This Week’s Finds in parallel, trying to tell a long story and make sure it’s told in detail.
Right now I just want to make sure I understand one thing. In their book Rational Homotopy Theory, Félix, Halperin and Thomas claim:
Proposition 26.4: If is a topological monoid, then the normalized singular chain complex is a differential graded Hopf algebra.
Now, there’s something puzzling about this right away. Following your instincts, when is a topological group you’d naturally expect to be a differential graded Hopf algebra. But when is just a topological monoid, you’d only expect to be a differential graded bialgebra — since where would the antipode come from, if not the inverse operation in ?
This puzzle is easily resolved: Félix et al define a differential graded Hopf algebra in a way that omits any mention of the antipode! So, they’re really getting a differential graded bialgebra.
But my real question concerns the Dold–Kan theorem, which is underlying the proof of this result.
November 26, 2009
What’s So Special About the Rationals?
Posted by David Corfield
I posed a question over at Math Overflow which netted me one useful answer from Andrew Stacey (along with my first nice question badge). Let’s see if the Café can help me with what I really want to know.
So, the rationals form the unique dense linearly ordered set without endpoints of countably infinite cardinality. On top of this we can build up compatible structure all the way to an ordered topological field. The rationals form the field of fractions of the integers, and the prime field for characteristic .
Newton Fellowships at Sheffield
Posted by Simon Willerton
If you have had at most two post-docs, are not a UK citizen and would like to do a post-doc in Sheffield then you might want to apply for a Newton fellowship.
The 50 Best Physics Blogs
Posted by John Baez
November 25, 2009
Combinatorial Model Categories
Posted by Urs Schreiber
Over the last years Jeff Smith has been thinking about – and notably talking about – but not publishing about – the idea and the theory of a certain type of model category called
While he himself didn’t publish, the theory was found to be very useful and bits and pieces of it appear now more or less scattered in the works of other authors.
As far as I can tell the earliest published reference of the central recognition result for combinatorial model categories – now widely known as Jeff Smith’s theorem – is Tibor Beke’s Sheafifiable homotopy model categories.
Apart from helping find various new interesting model category structures, this and related (unpublished) results made Dan Dugger understand that the local projective model structures on simplicial presheaves which he had been studying exhaust precisely all (simplicially enriched) combinatorial model categories:
(Dan Dugger’s theorem) combinatorial model categories are precisely (up to Quillen equivalence) the
of the global projective model structures on functors from a small category to the category of simplicial sets.
I can’t know if it’s close to the way it happend, but if you read Jacob Lurie’s book Higher Topos Theory backwards, starting with the very last three propositions of the appendix, you can read it as the result of taking Dan Dugger’s theorem in Jeff Smith’s theory and finding its intrinsic model independent version:
Simplicial combinatorial model categories are precisely the models for locally presentable -categories: those that are localizations – i.e. reflective -subcategories – of -categories of -presheaves.
(Among these the left exact localizations are precisely the -stack -toposes.)
In total this provides us with the optimal situation where on the one hand we have a comprehensive abstract nonsense picture that tells us what is going on globally, while on the other hand we have highly developed concrete models and tools for realizing this abstract nonsense: the theory of combinatorial model categories.
Accordingly, we are eagerly awaiting Jeff Smith’s book to appear, whose upcoming existence keeps being hinted at in the literature. While that is not available yet, I thought it might be worthwhile to start compiling the available material in a useful coherent fashion at one place. First steps in this direction are at combinatorial model category and Bousfield localization of model categories.
One very useful input I already got on this was very kindly from Denis-Charles Cisinki, who pointed out the semi-published document by Clark Barwick: On left and right model categories and left and right Bousfield localization. Parts of that I have used in the construction of these entries. (All nonsense and other imperfections, of which there is still plenty, is my fault.) Much more needs to be done.
This Week’s Finds in Mathematical Physics (Week 284)
Posted by John Baez
In week284 of This Week’s Finds, see Greg Egan’s new proofs of a theorem that goes back at least to 300 BC. One proof uses the fact that these triangles are congruent:
Another uses golden triangles. Then, hear about one day of the special session on homotopy theory and higher algebraic structures at UC Riverside. Categorified quantum groups, the Halperin-Carlsson conjecture, real Johnson-Wilson theories, Picard 2-stacks, quasicategories, motivic cohomology theory, and toric varieties — we got bombarded by all these concepts, and now you will too!
November 23, 2009
Equipments
Posted by Mike Shulman
I mentioned in my intro that as wonderful as -categories are, they’re really just one (important) part of the zoo of “higher categorical structures” out there. Today I want to tell you about another inhabitant of that zoo: a wonderful gadget called a proarrow equipment (or just an equipment), which lets us do what I call “formal category theory.” Equipments don’t seem to be very well-known, especially in the northern hemisphere (even though their inventor, R.J. Wood, is a Canadian at Dalhousie), but there are some indications that they’re gaining ground, so I’m doing my best to help them along.
This post will be a lightning-fast introduction to formal category theory in equipments. But I’m going to present the definition in a nonstandard way, because it turns out that an equipment is basically the same as what I’ve called a framed bicategory, and I find that way of thinking about it more natural—and also easier to generalize (but that’s another post). Some of it may go by a little quickly, but I think it’s the sort of thing that’s really quite fun to work out yourself once you’ve been pointed in the right direction.
November 19, 2009
Mathematical Emotion
Posted by David Corfield
Continuing the season of Collingwood on mathematics, here is an extract from The Principles of Art (1938):
A symbol is language and yet not language. A mathematical or logical or any other kind of symbol is invented to serve a purpose purely scientific; it is supposed to have no emotional expressiveness whatever. But when once a particular symbolism has been taken into use and mastered, it reacquires the emotional expressiveness of language proper. Every mathematician knows this. At the same time, the emotions which mathematicians find expressed in their symbols are not emotions in general, they are the peculiar emotions belonging to mathematical thinking. (p. 268)
[‘Symbol’ is used here to mean “something arrived at by agreement and accepted by the parties to the agreement as valid for a certain purpose” (p. 225).]
Anyone who doubts such ‘emotions belonging to mathematical thinking’ exist need only read an edition or two of This Week’s Finds. They are dripping with emotion, as the modern phrase has it.
November 18, 2009
Cobordism and Topological Field Theories Week 3
Posted by Alexander Hoffnung
Welcome to week 3 of the cobordism and TFT seminar at UCR. The previous lecture by Julie Bergner can be found here. There she talked about categories of cobordisms.
In the present lecture, Julie introduces symmetric monoidal categories and defines a notion of topological field theory.
To keep everyone apprised of the state of this seminar, I should say that in “real time” we are about to hit week 9. In “blog time” we are still not caught up, but I am sure we will get there soon. The nice thing is that I can give you a preview of the weeks to come below the fold.
November 16, 2009
Combinatorial-Game Categories
Posted by Mike Shulman
I just got back from the category theory Novemberfest at CMU, which was plenty of fun. One especially nice talk was by Geoff Cruttwell, who talked about axiomatizing the structure that exists on Joyal’s category of combinatorial (Conway) games. It turns out that the category of (finite) games is initial among such “combinatorial-game categories,” which implies a clever way to construct invariants of games. And naturally, the question of a terminal object is related to ill-founded or infinite games.
A Rose by Any Other Name
Posted by David Corfield
Pity Ola Bratteli who, when checking out how cited he is, has to take into account the “common misspellings Bratelli, Brattelli and the less common Brateli and Blatteli” of his last name. For someone who has given his name to the rather important Bratteli diagram, this is unfortunate.
Bratteli diagrams are ways of depicting approximately finite -algebras.
November 13, 2009
The 1000th Post on the n-Category Cafe
Posted by John Baez
Whoo-hoo! It’s our 1000th post! ![]()

We’ve got four new hosts at the café, and we’d like you to meet them…
November 11, 2009
This Week’s Finds in Mathematical Physics (Week 283)
Posted by John Baez
In week283 of This Week’s Finds, see galaxies in visible, infrared, and ultraviolet light:

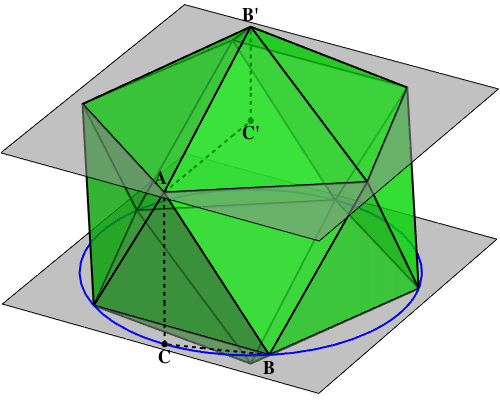
Read the mystery of who discovered the icosahedron: Theaetetus or the ancient Scots. Read about Lieven le Bruyn’s detective work which helped solve this case! And learn an amazing fact, proved in the last book of Euclid’s Elements, which relates regular polygons with 5, 6, and 10 sides.
November 10, 2009
Courant Algebroids From Categorified Symplectic Geometry
Posted by John Baez
guest post by Chris Rogers
‘Higher symplectic geometry’ is a topic that has come up recently in posts here in the -Café and in some ideas presented by Urs and others in the Lab. This is a subject I’ve been thinking a lot about lately, and I just finished a (rough!) draft of a paper that attempts to establish some connections between two different approaches to generalizing, extending, and/or categorifying symplectic geometry. So of course I happily accepted John’s invitation to write a guest post about some of this work. I hope by doing so I can contribute a little something to the ongoing discussion and learn more about the different ideas people have on the subject.
November 6, 2009
Fraïssé Limits
Posted by David Corfield
The Rado graph, or random graph, seems to be an extraordinary entity. Take countably many nodes, then for each pair of nodes flip a coin and if it shows heads, draw an edge between them. Almost surely you will have generated the Rado graph, .
Any finite graph (and indeed any countable graph) is contained in , not just in the sense of being embeddable, but in the sense of being an induced subgraph, that is, it is the full subgraph on a subset of nodes. Along with this universality, is also homogenous in the sense that any isomorphism between finite induced subgraphs extends to an automorphism of all of .
is very robust, you can delete finitely many vertices, add or remove finitely many edges, or interchange edges and non-edges, and you still end up with a graph isomorphic to . Furthermore, the odd thing about the construction of this graph is that I didn’t have to tell you the probability of the coin showing heads. So long as is in and the tosses are independent, the Rado graph almost surely emerges.
Not only this, there are many ways to generate it without using random devices. Rado himself took the nodes to be the natural numbers, and an edge between and whenever either the th bit of the binary representation of is nonzero, or the th bit of the binary representation of is nonzero. Yet another method has us take as nodes the prime numbers equal to 1 mod 4. Then we join and if they are quadratic residues of each other.
November 4, 2009
Who Discovered the Icosahedron?
Posted by John Baez
This weekend we’re having a meeting of the American Mathematical Society here at Riverside. Julie Bergner and I are running a special session on Homotopy Theory and Higher Algebraic Structures, and there will also be two special sessions on knot theory, one run by Alissa Crans and Sam Nelson. It should be fun! And it’s starting already: Khovanov will be giving a colloquium talk today.
Notions of Space
Posted by Urs Schreiber
Today is my turn in our Seminar on A Survey of Elliptic Cohomology.
I attempted to write a survey of some central ideas in Jacob Lurie’s Structured Spaces.
You can find it here: Notions of Space.
An Adventure in Analysis
Posted by Tom Leinster
One reason I went into category theory is that I wanted a subject that would take me to different parts of the mathematical world. These last few weeks I’ve been getting my wish in spades. My hard drive contains 53 analysis papers and books that three weeks ago it didn’t. My desk is piled with library books. My floor is a mess of handwritten notes covered in integral signs.
What prompted this adventure in analysis was a problem about magnitude of metric spaces. Thanks to the contributions of a whole crowd of people, the problem has now been solved. The problem-solving process, here and at Math Overflow, took all sorts of twists and turns, many of them unnecessary. But I think I can now present a fairly straight path to a solution. To thank those who contributed — and to entertain those who were half-interested but didn’t have the energy to keep up — I give you an overview of the problem and its solution.
November 3, 2009
The Arrow of Time in Cat
Posted by David Corfield
Back here we were talking about the symmetry-breaking that takes place in mathematics by the choice of working in , which John attributed to nothing less than the ‘arrow of time’.
Why do many-to-one but not one-to-many relations get singled out for single treatment and dubbed ‘functions’? Because functions are supposed to be ‘deterministic’: the cause must determine the effect. We don’t care if the effect fails to determine the cause.
Now what is there to be said about the 2-category Cat and its three duals: , and ?
November 2, 2009
Interview with Manin
Posted by John Baez
Try this interview with Yuri Manin:
- Mikhail Gelfand, We do not choose our profession, it chooses us: interview with Yuri Manin, translated by Mark Saul, Notices of the AMS 56 (November 2009), 1268–1274.
Manin is most famous for his work on number theory and algebraic geometry. But he’s also famous for his work on noncommutative geometry, the self-dual solutions of the Yang–Mills equations, and much more. He was wide interests and erudition to spare, so it’s interesting to read his view on the history of mathematics, and its future. Check out his remarks on Feynman integrals as an ‘Eiffel tower hanging in the air with no foundation’, the role of Edward Witten in modern mathematics, and the trend towards the ‘homotopification’ of mathematics.
 Posts with this logo use
Posts with this logo use 














