April 19, 2017
Functional Equations, Entropy and Diversity: A Seminar Course
Posted by Tom Leinster
I’ve just finished teaching a seminar course officially called “Functional Equations”, but really more about the concepts of entropy and diversity.
I’m grateful to the participants — from many parts of mathematics, biology and physics, at levels from undergraduate to professor — who kept coming and contributing, week after week. It was lots of fun, and I learned a great deal.
This post collects together all the material in one place. First, the notes:
- Tom Leinster, Functional Equations. Rough and ready course notes, University of Edinburgh, 2017.
Now, the posts I wrote every week:
- I. Cauchy’s equation
- II. Shannon entropy
- III. Explaining relative entropy
- IV. A simple characterization of relative entropy
- V. Expected surprise
- VI. Using probability theory to solve functional equations
- VII. The -norms
- VIII. Measuring biodiversity
- IX. Entropy on a metric space
- X. Value
- XI. The diversity of a metacommunity
The Diversity of a Metacommunity
Posted by Tom Leinster
The eleventh and final installment of the functional equations course can be described in two ways:
From one perspective, I talked about conditional entropy, mutual information, and a very appealing analogy between these concepts and the most basic primary-school Venn diagrams.
From another, it was about diversity across a metacommunity, that is, an ecological community divided into smaller communities (e.g. geographical sites).
The notes begin on page 44 here.
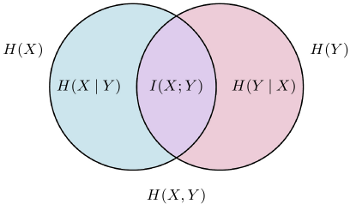
April 17, 2017
On Clubs and Data-Type Constructors
Posted by Emily Riehl
Guest post by Pierre Cagne
The Kan Extension Seminar II continues with a third consecutive of Kelly, entitled On clubs and data-type constructors. It deals with the notion of club, first introduced by Kelly as an attempt to encode theories of categories with structure involving some kind of coherence issues. Astonishing enough, there is no mention of operads whatsoever in this article. (To be fair, there is a mention of “those Lawvere theories with only associativity axioms”…) Is it because the notion of club was developed in several stages at various time periods, making operads less identifiable among this work? Or does Kelly judge irrelevant the link between the two notions? I am not sure, but anyway I think it is quite interesting to read this article in the light of what we now know about operads.
Before starting with the mathematical content, I would like to thank Alexander, Brendan and Emily for organizing this online seminar. It is a great opportunity to take a deeper look at seminal papers that would have been hard to explore all by oneself. On that note, I am also very grateful for the rich discussions we have with my fellow participants.
April 14, 2017
Value
Posted by Tom Leinster
What is the value of the whole in terms of the values of the parts?
More specifically, given a finite set whose elements have assigned “values” and assigned “sizes” (normalized to sum to ), how can we assign a value to the set in a coherent way?
This seems like a very general question. But in fact, just a few sensible requirements on the function are enough to pin it down almost uniquely. And the answer turns out to be closely connected to existing mathematical concepts that you probably already know.
April 5, 2017
Applied Category Theory at UCR (Part 1)
Posted by John Baez
The American Mathematical Society is having a meeting here at U. C. Riverside during the weekend of November 4th and 5th, 2017. I’m organizing a session on Applied Category Theory, and I’m looking for people to give talks.
Functional Equations IX: Entropy on a Metric Space
Posted by Tom Leinster
Yesterday’s functional equations class can be described in two ways:
From a mathematical point of view, I gave a definition of the entropy of a probability distribution on a metric space. The high point was a newish maximum entropy theorem (joint work with Mark Meckes).
From a biological point of view, it was all about measuring the diversity of a community in a way that factors in the varying similarity between species. This approach is well-adapted to situations where there’s no clear division into “species” — for instance, communities of microbes. It also addresses a point made yesterday on this blog. All this is based on joint work with Christina Cobbold.
You can read the notes from yesterday’s class on pages 35–38 here.
April 4, 2017
Elementary (∞,1)-Topoi
Posted by Mike Shulman
Toposes come in two varieties: “Grothendieck” and “elementary”. A Grothendieck topos is the category of sheaves of sets on some site. An elementary topos is a cartesian closed category with finite limits and a subobject classifier. Though these definitions seem quite different, they are very closely related: every Grothendieck topos is an elementary topos, while elementary toposes (especially when considered “over a fixed base”) behave very much like Grothendieck ones.
All the fervor about -toposes nowadays has centered on Grothendieck ones: -categories of -sheaves of -groupoids on -sites. (Technically, this is only true if we use a perhaps-excessively-general notion of “site”, but it’s the right idea.) However, it’s quite natural to speculate about a corresponding notion of elementary -topos. Because an elementary 1-topos is essentially “a category whose internal logic is intuitionistic higher-order type theory”, it’s natural to try to define an elementary -topos to be an -category whose “internal logic” is, or at least should be, a kind of homotopy type theory. However, even laying aside the unresolved questions involved in the “internal logic” of -categories, it’s never been entirely clear to me exactly what “kind” of homotopy type theory we should use here.
Until now, that is. I propose the following definition: an elementary (∞,1)-topos is an -category such that
- It has finite limits and colimits (in the -sense, i.e. homotopy limits and colimits).
- It is locally cartesian closed.
- It has a subobject classifier, i.e. a map such that for any the hom--groupoid is equivalent, by pullback of , to the -groupoid of subobjects of (which is equivalent to a discrete set). Here a “subobject” is a map such that each -functor is fully faithful.
- For any morphism , there exists an object classifier that classifies (i.e. is a pullback of ) and such that the collection of morphisms it classifies (i.e. the pullbacks of ) is closed under composition, finite fiberwise limits and colimits, and dependent products. Here is an “object classifier” if for any , pullback of yields a fully faithful functor from to the core (the maximal sub--groupoid) of the slice -category over .
April 3, 2017
Gluing Together Finite Shapes with Kelly
Posted by Emily Riehl
Guest post by David Jaz Myers
The Kan Extension Seminar continues with Kelly’s Structures defined by limits in the enriched context, I, or as I like to call it, Presenting categories whose objects are glued together out of finite shapes. This paper hit the presses in 1982 and represented both a condensation and generalization of the theory of locally finitely presentable categories. Kelly achieved both the condensing and the generalizing through his use of weighted (or, as he calls them, indexed) limits and colimits. The resulting theory is slick and highly categorical, but very dense. So, in this post, we’re going to button down a bit and skim over a few details so that we can focus on the story and the powerful results which sustain it, rather than the technicalities. I will label the propositions by where they appear in Kelly’s paper, so that you can find the technicalities if you would like.
At first, it will seem like this post is a radical departure from the previous seminar posts. But as we go on, we’ll see that gluing together finite shapes has a lot to do with the categorical approach to algebra that Evangelia wrote about in the post that kicked off our seminar.
Before I start, I’d like to thank Emily, Alexander, and Brendan for organizing this lovely seminar and inviting me to participate. I’d also like to thank my fellow students for their insight and conversation.
Enrichment and its Limits
Posted by Emily Riehl
Guest post by David Jaz Myers
What are weighted limits and colimits? They’re great, that’s what!
In this post, we prepare for the next part of the Kan Extension Seminar by learning a bit about enrichment and weighted limits and colimits. I’ll also describe the “ point of view” that I’ll be adopting for the next post.
April 1, 2017
Jobs at U. C. Riverside
Posted by John Baez
The Mathematics Department of the University of California at Riverside is trying to hire some visiting assistant professors. We plan to make decisions quite soon!
The positions are open to applicants who have PhD or will have a PhD by the beginning of the term from all research areas in mathematics. The teaching load is six courses per year (i.e. 2 per quarter). In addition to teaching, the applicants will be responsible for attending advanced seminars and working on research projects.
This is initially a one-year appointment, and with successful annual teaching review, it is renewable for up to a third year term.
For more details, including how to apply, go here:
https://www.mathjobs.org/jobs/jobs/10162
 Posts with this logo use
Posts with this logo use 














