September 24, 2013
Clay Mathematics Conference
Posted by John Baez
A while back, Bruce Bartlett announced a Workshop on Quantum Mathematics and Computation at Oxford. But that’s part of a bigger thing:
• Clay Research Conference, September 29 – October 4, 2013, Oxford University.
The Definition of Graph is Classified
Posted by Tom Leinster
Amid the (to me, highly disturbing) news that the state apparatuses of the US and UK have been secretly and systematically keeping records of our emails, our web browsing, our phone calls, our letters, our financial transactions and our physical location, here’s one half-smile’s-worth of light relief: the definition of graph is classified as “Top Secret”. (Update: or maybe not. See Tod’s comment below.)
(Click to see the news article this comes from, and to expand the tiny writing along the top and bottom which specifies the precise degree of top-secretness.)
This NSA slide uses the category theorists’ word object for a vertex of a graph. I’m relieved they don’t call the edges morphisms.
September 19, 2013
New Teaching Method Improves Math Skills
Posted by Simon Willerton
My attention was grabbed by the following press release from the University of Florida: New Teaching Method Improves Math Skills, Closes Gender Gap in Young Students.
It begins with an overview.
When early elementary math teachers ask students to explain their problem-solving strategies and then tailor instruction to address specific gaps in their understanding, students learn significantly more than those taught using a more traditional approach. This was the conclusion of a yearlong study of nearly 5,000 kindergarten and first-grade students conducted by researchers at Florida State University.
I was rather surprised that trying to figure out what a student does and does not understand counts as a new teaching method.
[The researchers] drew upon research demonstrating that the learning of mathematics is facilitated when teachers gain deeper insights into what their students already know and are able to do as well as what students do not know and are unable to do. Teachers gather these insights through careful observation and by engaging students in discussions of their mathematical thinking.
The question that jumps out here is “If this is a revolutionary insight then what is the more traditional approach to teaching maths?” Well, apparently it’s that
teachers typically rely heavily on a math textbook to guide the planning of day-to-day instruction and often provide students feedback only on whether their answers are correct.
I suppose that I shouldn’t be surprised by this as, thinking closer to home, this ‘traditional approach’ can also be found at higher levels and I often encounter a perception that maths is just about getting the right answer.
The system that has been developed is called the Mathematics Formative Assessment System (MFAS) and details are available on the MFAS website. I can only wish good luck to the people involved in this.
September 17, 2013
Integral Octonions (Part 6)
Posted by John Baez
You can add and subtract integers. You can multiply them. You can also think about them geometrically, as a lattice in the real line.
The same is true for the Gaussian integers in the complex plane:
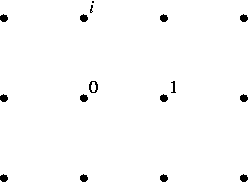
or, for that matter, the Eisenstein integers:
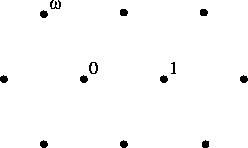
Things get even more interesting for the quaternions and octonions. There are various different concepts of ‘integer’ for these number systems, but I’m especially interested in the so-called ‘Cayley integral octonions’, because they’re the most exotic and mysterious of the lot.
When it comes to their additive and geometrical aspects, the Cayley integers look just like the lattice in an 8-dimensional Euclidean vector space, rescaled so that the shortest nonzero vectors have length 1. In Parts 3, 4 and 5 of this series we studied these aspects in loving detail. You can now see all the previous parts in one place here.
Now I’d like to finally get around to discussing the multiplicative structure of the Cayley integers.
September 16, 2013
Mapping (Co)cylinder Factorizations via the Small Object Argument
Posted by Emily Riehl
I’ve been thinking about the small object argument recently and noticed something curious. Even though I can’t think of any applications, I still find it interesting. Fortunately, the -Category Café seems like the perfect place to record curiosities.
Here I don’t mean Quillen’s small object argument but rather an improved construction due to Richard Garner. And I don’t quite mean the functorial factorization he describes in his paper but rather an enriched version that you can read more about in chapter 13 of these notes.
The reason I like the calculation I’m about to describe is that it illustrates that what I might call the enriched algebraic small object argument can be remarkably computable. Like Quillen’s original construction, this form of the small object argument produces a factorization into a pair of maps whose lifting properties can be easily characterized. But the algebraic small object argument always converges and sometimes you get lucky and the factorization it spits out, rather than being some transfinite beast, instead turns out to be the elementary functorial factorization you already had in mind.
September 12, 2013
Classical Dualities and Formal Concept Analysis
Posted by Simon Willerton
What do the algebraic varieties, convex sets, linear subspaces, real numbers, logical theories and extension fields have in common with the formal concepts that I was discussing last time? Well, they can all be constructed in the same way.
Last time I described how if you start of with two sets together with a relation between them then you can turn a handle on a machine and out will pop a partially ordered set of ‘concepts’. Each concept is a pair consisting of a subset of each of the two original sets. This results in a duality, or more precisely a Galois correspondence, between certain subsets (the ‘closed’ ones) of the the original sets.
I didn’t realise that many standard dualites in mathematics arise in this way, just starting with two sets and a relation between them. This struck me when John was questioning me about my previous post.
See if you can guess which concepts or dualities emerge from the following relations. The answers are below the fold.
Algebraic geometry Take (the underlying set of) and the set of complex polynomials in -variables with the relation that the polynomial vanishes at the point.
Number theory Take the set of points in a field where is a finite Galois extension , and the set of field automorphisms of which fix , with the relation that the automorphism fixes the point.
Linear algebra Take a vector space and the dual vector space with the relation that the function vanishes at the point.
Logic Fix a formal language . Take the set of -structures and the set of -sentences with the relation expressing the truth of a sentence with respect to a structure.
Convex geometry Take the set of points of an affine space (e.g. ) and the set of closed halfspaces in with the relation that the point is in the halfspace.
Analysis Take the set of rational numbers and the set of rational numbers again, with the relation being .
[This isn’t what I said I’d talk about this time, but I got distracted!]
Good Mathematics
Posted by David Corfield
I’m speaking next week at a conference in London addressing the issue of values in mathematics. The thrust of my talk will be that any satisfactory discussion of this topic must include the very largest units of assessment, long-term research programmes, and these in turn can only be assessed in terms of the place they come to occupy in the history of the subject.
I’ll take this quotation from Alasdair MacIntyre as my point of departure:
Let me cast the point I am trying to make about Galileo in a way which, at first sight, is perhaps paradoxical. We are apt to suppose that because Galileo was a peculiarly great scientist, therefore he has his own peculiar place in the history of science. I am suggesting instead that it is because of his peculiarly important place in the history of science that he is accounted a peculiarly great scientist. The criterion of a successful theory is that it enables us to understand its predecessors in a newly intelligible way. It, at one and the same time, enables us to understand why its predecessors have to be rejected or modified and also why, without and before its illumination, past theory could have remained credible. It introduces new standards for evaluating the past. It recasts the narrative which constitutes the continuous reconstruction of the scientific tradition. (The Tasks of Philosophy, p. 11)
September 10, 2013
CRM (Centre de Recherches Mathématiques, Montreal) Thematic Semester “New Directions in Lie Theory
Posted by Alexander Hoffnung
Much like folks around here, Alistair Savage has been thinking about categorification for some time now and has together with Erhard Neher announced an upcoming opportunity for graduate students and postdocs to take part in a winter school as part of the CRM (Centre de Recherches Math`ematiques, Montreal) Thematic Semester “New Directions in Lie Theory” from January to June 2014.
The first winter school will take place January 6-17, 2014 and will feature two courses:
Introduction to categorification, taught by Alistair Savage
Introduction to Kac-Moody and related Lie algebras, taught by Erhard Neher
Further information can be found at: http://www.crm.umontreal.ca/2014/Catego14/index_e.php.
It is worth following the above link as Alistair has begun to post some information as well as his reference materials, which may be of interest so I will repost here
- Alexander Kleshchev, Linear and projective representations of symmetric groups, Cambridge University Press, 2009.
- Volodymyr Mazorchuk, Lectures on algebraic categorification, European Mathematical Society, 2012.
- Wei Lu and Aaron McBride, Algebraic structures on Grothendieck groups, 2013.
There is funding available for graduate students and postdocs to attend the winter school. Applications for funding can be submitted online at the above website. The deadline is October 1, 2013.
Information on the thematic semester (including the second winter school) can be found at http://www.crm.math.ca/LieTheory2014/.
Please pass this information on to students and postdocs and anyone else that you think might be interested.
September 3, 2013
Integral Octonions (Part 5)
Posted by John Baez
I’m back from China. I saw lots of cool stuff:
(Click for more information.)
But I also had lots of time sitting in trains, buses and automobiles to think about the root polytope. Calculations along these lines turn out to be a great antidote to boredom!
So now I’d like to show you how to calculate the number of vertices, edges, 2d faces, etc. of this 8-dimensional polytope. What’s interesting is not the answers so much as the technique, which involves Dynkin diagrams.
September 2, 2013
Formal Concept Analysis
Posted by Simon Willerton
Last time I posted about the nucleus of enriched functors. This time I will post about something a bit (!) less abstract — formal concept analysis — something which has applications in data-mining, software engineering and, possibly, catching terrorists. Next time I’ll post about how these two things come together and can give rise to fuzzy concept analysis.
Formal concept analysis is about extracting the relationships and hierarchies available from the common attributes shared by objects. Let’s try to break up this abstract definition with a concrete example.
In the most basic form of formal concept analysis, the input consists of a set of objects (from the German ‘Gegenstände’), a set of attributes (from the German ‘Merkmale’) and a relation (from the German ‘Inzidenzrelation’) between the objects and the attributes expressing which objects have which attributes. This triple is called the formal context and is often expressed as a table. I don’t feel witty enough today to think up a pertinent Café-based example, so instead I will steal a standard example from the formal concept analysis literature. Here is the table.
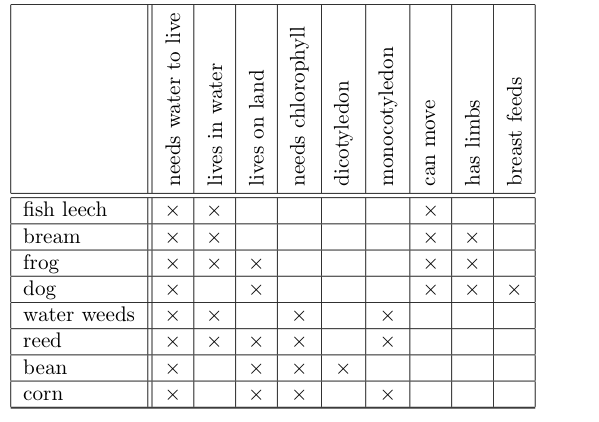
[For non-native English speakers, bream is a kind of fish.]
The output of the analysis is the concept lattice (from the German ‘Begriffsverband’). This is a lattice, which means it is a poset in which each pair of elements have a greatest lower bound and a least upper bound. The concept lattice expresses relationships between the objects and the attributes. Here is the concept lattice for the above example.
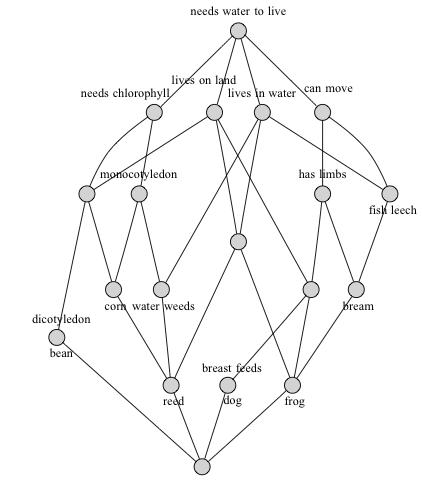
I will explain how you go from the formal context to the concept lattice in the main body below. The relation with my last post is contained in the following slogan.
The concept lattice is the nucleus of the relation .
This comes about by thinking about everything here as being done in the realm of categories enriched over truth values. I’ll explain that next time, but many of you will be able to see that in what you read here.
 Posts with this logo use
Posts with this logo use 


















