December 30, 2007
Non-Mathematician Rediscovers Rn, Cn
Posted by John Baez
I did a lot of historical reading about Hamilton, quaternions and the like when writing my review article about the octonions. When Hamilton invented the quaternions in 1843, it was a big deal: people hadn’t realized you could just make up new rules for multiplication. A lot of people joined in the fun, inventing their own hypercomplex number systems. Most of these systems aren’t terribly interesting. Hamilton’s pal John T. Graves found one of the really special ones: the octonions. Clifford found a whole bunch. But in general, most mathematicians now prefer to study hypercomplex number systems en masse rather than individually. They’re now called “real algebras”, and there are lots of nice general theorems about them.
This does not prevent amateurs from continuing to invent hypercomplex number systems and become excited about them. An amusing example was brought to my attention by David Farrell:
- Rodney Rawlings, Non-mathematician devises hypercomplex numbers, with possible implications for mathematics and the philosophy of science.
Brace yourself: Rawlings links his discovery to the Objectivist philosophy of Ayn Rand!
Transgression of n-Transport and n-Connections
Posted by Urs Schreiber
Since it will play a role both for what is currently indicated in section 5 of the article on Lie -algebra connections and their application to String- and Chern-Simons -transport as well as for the next followup of my work with Konrad Waldorf, I am thinking again in more detail about
Trangression of -transport and -connections
Abstract. After going through some ground work concerning generalized smooth spaces and their differential graded commutative algebras of forms, I talk about the issue of transgression of transport -functors and Lie -valued -connections to smooth mapping spaces.
This builds on the general idea of -functorial transgression as the image of an internal hom as first voiced in this old comment and then later incorporated in the discussion of The charged -particle and detailed a bit more in the entry Multiplicative Structure of Transgressed -Bundles.
Currently only a few sketches are present in the above pdf, as I am going to develop this as we go along.
One important aspect, emphasized in the above abstract, is that the discussion greatly profits from a good general understanding of the relation between generalized smooth spaces and their differential graded-commutative algebras of differential forms. I started making comments on that here and now Todd Trimble thankfully chimed in by providing this detailed reply, which I will reproduce below.
But first, I’ll reproduce the introductory remarks from my notes to set the stage.
December 29, 2007
BF-Theory as a Higher Gauge Theory
Posted by Urs Schreiber
I’ll quickly say a couple of words on the occasion of
F. Girelli, H. Pfeiffer, E. M. Popsecu
Topological Higher Gauge Theory - from BF to BFCG theory
arXiv:0708.3051
about the interpretation of the class of topological field theories known as BF-Theory, motivated also by the results Jim, Hisham and myself are talking about in Lie -Connections and their Application to String- and Chern-Simons -Transport.
It’s about if and how exactly to interpret the BF-theory Lagrangian as a functional on Lie -algebra valued forms.
The QG-TQFT Blues
Posted by John Baez
Here at last is the music video we’ve all been waiting for!
- Professor Elvis Zap, The Quantum Gravity Topological Quantum Field Theory Blues.
Elvis Zap, also known as Scott Carter, is a quantum topologist from way down south. He’s one of the guys who first got me interested in possible applications of higher-dimensional knot theory to quantum gravity. That eventually led me to -categories, and I’ve been on a downhill slide ever since. I know the blues he’s singin’ about.
Lyrics follow… and more.
December 28, 2007
Challenges for the Future
Posted by David Corfield
Benjamin Mann of DARPA has constructed a list of 23 challenges for mathematics over the next century.
Whereas Hilbert notes about his 23 problems
I have generally mentioned problems as definite and special as possible, in the opinion that it is just such definite and special problems that attract us the most and from which the most lasting influence is often exerted upon science,
Mann’s challenges are generally open-ended, resembling Hilbert’s sixth problem:
6. Mathematical treatment of the axioms of physics
The investigations on the foundations of geometry suggest the problem: To treat in the same manner, by means of axioms, those physical sciences in which mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.
rather than his thirteenth:
13. Impossibility of the solution of the general equation of the 7-th degree by means of functions of only two arguments.
Some motivation accompanies Mann’s list, but it would be good to see experts write a few paragraphs for each challenge on that inviting parchment background.
December 26, 2007
Geometric Representation Theory (Lecture 17)
Posted by John Baez
This time in the Geometric Representation Theory seminar, James Dolan explains ‘degroupoidification’ — the process of turning a span of groupoids into a linear operator between vector spaces. We’ve been telling people about this for a while now, for example in week256 of This Week’s Finds. But now Jim reveals more about what’s really going on.
December 25, 2007
Lie oo-Connections and their Application to String- and Chern-Simons n-Transport
Posted by Urs Schreiber
Hisham Sati, Jim Stasheff and myself are working on writing up some ideas on Lie -algebra cohomology and its application to String- and Chern-Simons -Transport, further exploring the second edge of the cube.
We would like to share this document:
H. Sati, J. Stasheff, U. S.
-algebra connections and applications to String- and Chern-Simons -Transport
arXiv:http://arxiv.org/abs/0801.3480
(pdf of the latest version)
This consists of three parts:
Part A : Overview and physical applications
Part B: Lie -algebras, their cohomology and their String-like extensions
Part C: Categorified Cartan-Ehresmann connections and lifts through String-like extensions.
This can be thought of as providing details to the discussion provided in my slide show String- and Chern-Simons -Transport. -Café regulars will recognize a certain synthesis of topics I used to discuss here, like inner automorphism -groups, String and Chern-Simons Lie -algebras, -Curvature , obstruction theory and other things. To some extent, the main idea here found its final form after John posed a nice problem in Higher Gauge Theory and Elliptic Cohomology.
Much progress on the relation of the general formalism to (heterotic) string theory and supergravity/M-theory occurred when I visited Hisham Sati in Yale. The full implications are only briefly indicated here.
We’d be grateful for whatever comment you might have.
This Week’s Finds in Mathematical Physics (Week 260)
Posted by John Baez
In week260 of This Week’s Finds, learn about the Vishniac instability in the Retina Nebula:
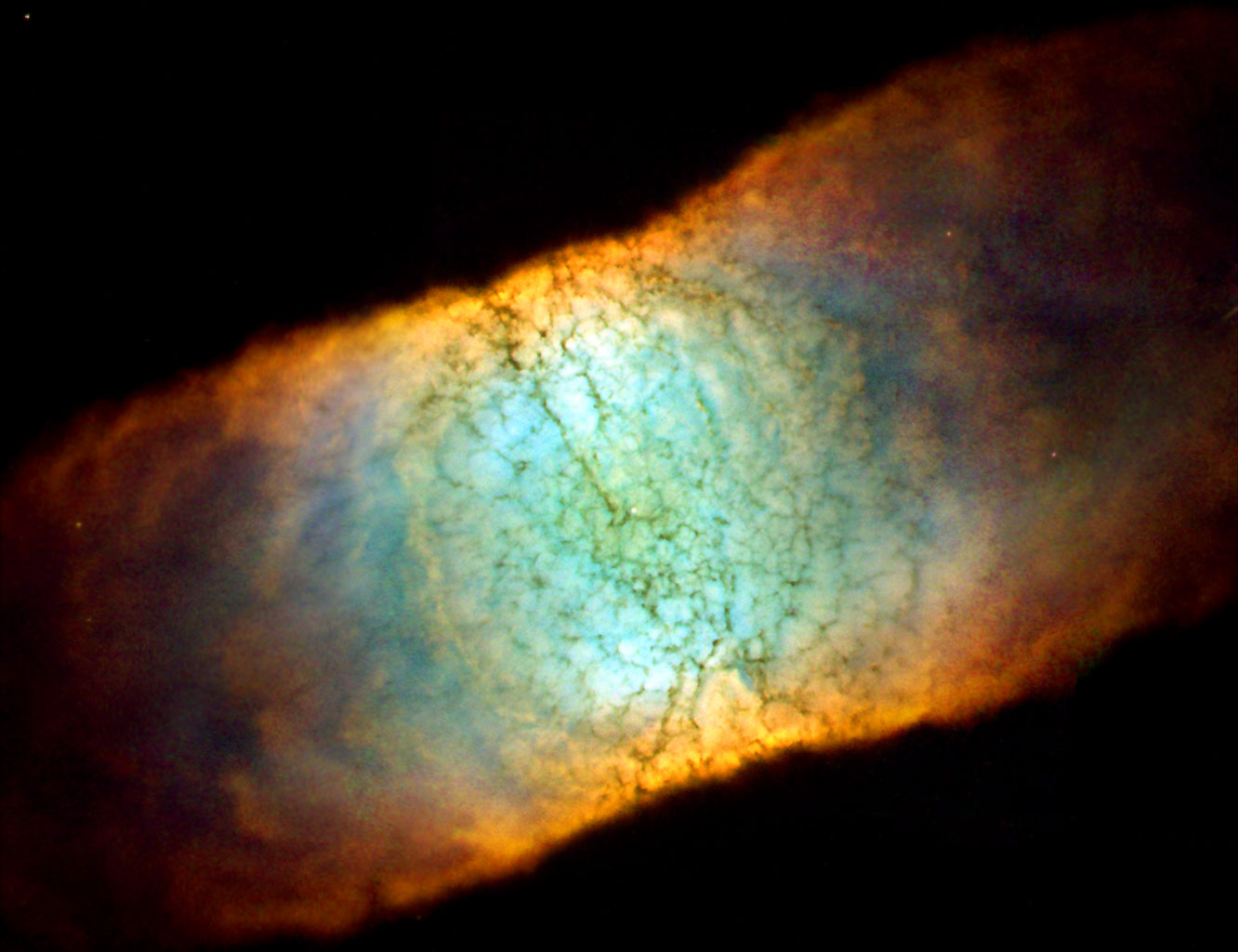
Then try my Christmas eve guide to free books on math and physics. There are more and more available! Soon those expensive textbooks will be obsolete. Here’s a nice illustration of Taylor series for the sine function, from Robert Nearing’s online book Mathematical Tools for Physics:

And finally: the ‘exceptional series’ of Lie algebras.
December 21, 2007
Roytenberg on Weak Lie 2-Algebras
Posted by John Baez
It’s been circulating informally since October, but now it’s available on the arXiv — a proposal for the definition of a fully general categorified Lie algebra!
- Dmitry Roytenberg, On weak Lie 2-algebras.
Abstract: A Lie 2-algebra is a linear category equipped with a functorial bilinear operation satisfying skew-symmetry and Jacobi identity up to natural transformations which themselves obey coherence laws of their own. Functors and natural transformations between Lie 2-algebras can also be defined, yielding a 2-category. Passing to the normalized chain complex gives an equivalence of 2-categories between Lie 2-algebras and 2-term “homotopy everything” Lie algebras; for strictly skew-symmetric Lie 2-algebras, these reduce to -algebras, by a result of Baez and Crans. Lie 2-algebras appear naturally as infinitesimal symmetries of solutions of the Maurer–Cartan equation in some differential graded Lie algebras and -algebras. In particular, (quasi-) Poisson manifolds, (quasi-) Lie bialgebroids and Courant algebroids provide large classes of examples.
Progic VI
Posted by David Corfield
I talked about Bayesian networks back here as a prelude to the shift from propositional to first-order relational structures. But before we take that step, it’s worth mentioning that there are other graphical models used in probabilistic reasoning. (If you prefer videos try this or this.)
In particular, there’s a class of models called Markov networks, which unlike Bayesian networks involve undirected edges. Given an undirected graph, a distribution is given by assigning non-negative real functions, , to cliques, , in the graph. These are called potential functions.
Then the probability of the node variables being in a given state is given by the product of the potential functions evaluated at the corresponding clique states, divided by a normalizing factor. All of which should put you in mind of certain models from statistical physics.
Non-Commutative Structures in Arithmetic and Geometry
Posted by Urs Schreiber
guest post by Minhyong Kim
In June of next year, the will be an informal workshop at University
College London on
Non-commutative structures in arithmetic and geometry
The idea is for a small group of experts from rather different areas to get together to explain to each other what it is they do, and possibly discover some unifying themes. The areas represented will be
Non-commutative Iwasawa theory, non-commutative geometry, non-abelian class field theory, non-abelian Hodge theory, Anabelian geometry, and, hopefully, some non-abelian physics.
A preliminary website is here .
Note also the related program at the Newton Institute.
Geometric Representation Theory (Lecture 16)
Posted by John Baez
Sick of Christmas shopping? Tired of the crowded malls, the rush, the commercialism? Take a break and learn some math! It’s free, it’s fun, and it’s good for you.
This time in the Geometric Representation Theory seminar, I start by quickly fixing the mistake I made when attempting to state the ‘Fundamental Theorem of Hecke Operators’ in lecture 14.
But then I begin the harder and more interesting job of trying to explain what’s really going on! Namely, ‘groupoidification’.
This is what our seminar is really about. We were just taking our time getting there, building up some of the key examples we’ll be using.
The first step is to see that groups acting on sets give groupoids. This nicely fits the idea of a groupoid as a ‘set with built-in symmetries’.
December 17, 2007
Basic Bundle Theory and K-Cohomology Invariants
Posted by Urs Schreiber
My friend Branislav Jurčo (who -Café regulars know from his Notes on Generalized Bundle Gerbes) has been working on a book on bundles and on K-theory. Now this is finally done:
Dale Husemöller, Michael Joachim, Branislav Jurco and Martin Schottenloher
Basic Bundle Theory and K-Cohomology Invariants
Lecture Notes in Physics 726, Springer-Verlag Berlin Heidelberg 2008
It even contains a discussion of String structures, which are really lifts to 2-bundles. (See also Jurčo on gerbes and stringy applications.)
Is Mathematics Special?
Posted by David Corfield
There’s to be a conference held in Vienna next May which asks Is Mathematics Special?
A bringing together of researchers from different fields interested in the question what makes mathematics special (if anything). Even if mathematics presents itself or is presented as a (quasi-)empirical matter, the status of an epistemic exception that mathematics forms among the sciences asks for explanations.
So, is mathematics special? Well, of course, any discipline is special. No other discipline than particle physics builds 27 km. long pieces of experimental apparatus. But one very noticeable feature of the Anglo-American philosophical treatment of mathematics is that it takes it to be a discipline very unlike the natural sciences. This divergence has developed out of the Russellian conviction that mathematics is a (dressed-up) form of logic, and so true in all possible worlds, while the sciences deal with particular empirical events in our universe.
There’s a quotation on the conference website from Felix Klein which suggests some will be looking to play down differences:
Quite often you may hear non-mathematicians, especially philosophers, say that mathematics need only draw conclusions from clearly given premisses and that it is irrelevant whether those premisses are true or false – provided they don’t contradict themselves. Anybody who works productively in mathematics, however, will talk in a completely different manner, In fact, those people base their judgements on the crystallized form in which mathematical theories are presented once they’ve been worked out. The research scientist, like any other scientist, does not work in a strictly deductive way but essentially makes use of his imagination and moves forward inductively with the help of heuristic aids.
Personally, given where we are today in philosophy, I should prefer people to side with Klein and attend to the similarities with other disciplines. In particular, we need to focus on what has been terribly neglected – mathematics’ higher-level aspirations. In its pursuit of phantoms, dreams, or vistas, my sense is that it is not so very different from other forms of intellectual enquiry.
John recommended a short article by Minhyong Kim – Mathematical Vistas – in which after a passage by Grothendieck the author says
It is hoped … that Grothendieck’s candid expressions might convey even to the casual reader that curious sense of the unknown attached to any process of deep learning and thinking, and the urgent conviction at the core of worthwhile endeavor.
If mathematics is special it’s because its practitioners have been deeply learning and thinking for such a very long time.
December 15, 2007
A Dialogue on Infinity
Posted by David Corfield
December 13, 2007
Geometric Representation Theory (Lecture 15)
Posted by John Baez
This time in the Geometric Representation Theory seminar, James Dolan begins the process of cleaning up the mess I made last time, when I was trying to state the ‘Fundamental Theorem of Hecke Operators’.
A quick and dirty fix is not hard. But a really beautiful and conceptually clear statement of this theorem takes more work. In fact, it’ll take the rest of this fall’s course! Jim begins by explaining why my statement was false. Then he turns to various forms of decategorification — as a warmup for the one we’ll need here, namely ‘degroupoidification’.
December 11, 2007
Program Geometry and Physics at HIM
Posted by Urs Schreiber
The (one year old) Hausdorff Research Institute for Mathematics

in Bonn is hosting a
Trimester Program on Geometry and Physics
May - August 2008
(poster)
I got one of the visitor positions there and hence will take a leave of absence from Hamburg for next summer. Looking forward to it, indeed.
For some reason the Hausdorff schedule is slightly out of sync with the semester here. It looks like during April 2008 I will therefore be employed neither here nor there.
I am just mentioning this in case somebody would like to invite me during April. If you have travel funds: I have time. ![]()
December 10, 2007
This Week’s Finds in Mathematical Physics (Week 259)
Posted by John Baez
In week259 of This Week’s Finds, hear what may be hiding in the Egg Nebula:

Then, learn how a mathematical phantom called the ‘field with one element’ is gradually becoming real. It may explain the deep inner meaning of q-deformation, and the 3-dimensional aspect of the integers!
December 9, 2007
Local Nets from 2-Transport
Posted by Urs Schreiber
While listening to AQFT talks last Friday I further developed the thoughts that I started talking about in
Oberwolfach CFT, Arrival Night, Algebra of Observables and Sheaves of Observables.
I wrote up a note in which the passage from -dimensional functorial QFT to the corresponding AQFT local net of observables is described in more detail:
On nets of local operators from 2-transport
Abstract. I would like to understand how the axioms of a local net of observable algebras follow from those of a transport -functor with values in -vector spaces. I suggest that local nets of algebras result when applying to an -vector transport a categorified version of the transition from the Schrödinger to the Heisenberg picture of quantum mechanics.
Here I consider some simple aspects of this question for . I show that every extended 2-dimensional QFT gives rise to a net of local monoids on 2-dimensional Minkowski space. The construction has an obvious generalization to arbitrary .
December 7, 2007
One Geometry (Math Raps)
Posted by John Baez
While Look Around You was a goofy parody of an old-fashioned BBC educational program on math, here’s a rap video with real mathematical content:
- Stephen Sawin, One Geometry: Perelman’s proof of the Poincaré conjecture, to the tune of Snoop Dogg and Pharrell William’s “Drop it Like it’s Hot”. Lyrics available here.
December 6, 2007
A Topos for Algebraic Quantum Theory
Posted by Urs Schreiber
I’ll try to summarize, very briefly, some key points of
Chris Heunen, Bas Spitters
A Topos for Algebraic Quantum Theory
arXiv:0709.4364v1 [quant-ph]
following up on our discussion of The Principle of General Tovariance.
(John Baez talked about Heunen&Spitters’ work in week 257.)
Progic V
Posted by David Corfield
I’ve come across something promissing for the Progic project. Apparently there is a way to complete the analogy:
propositional logic : predicate logic :: Bayesian networks: ?
The answer, it is claimed, is ‘probabilistic relational models’. Now before we take a look a them, it would be worth considering in what sense Bayesian networks are propositional.
And before that we need to know what a Bayesian network is. Well, first of all, it’s a directed acyclic graph (DAG), so a graph with directed arrows, and no cycles. Each vertex corresponds to a variable which may take any of a set of values, e.g., , taking values in . A ‘parent’ of vertex is a vertex with an edge pointing from it to . Then the final ingredient for a Bayesian network is a conditional probability distribution for each vertex given its parents, .
December 5, 2007
The Principle of General Tovariance
Posted by Urs Schreiber
Next Friday Klaas Landsman will give a talk here on
The principle of general tovariance: Physical laws should look the same in whatever topos they are defined.
He has made nice slides available online.
In my words, what “tovariance” is supposed to mean is this:
A physical theory should be formulated internally in terms of “arrow theory”: a physical theory should be an abstract diagram with certain properties (usually: some parts of it are required to be certain limits or colimits), such that it may be internalized (interpreted) in a suitable ambient category.
“Suitable” ambient categories might in particular be topoi. Or maybe just Barr exact categories (as in Glenn’s Realization of cohomology classes in arbitrary exact categories) as Igor Baković kindly emphasized to me.
Therefore “the principle of general tovariance” is close to my heart. I have talked about attempts to extract the right arrow theory of quantum field theory of -model type (including all gauge theories) in the series on the charged quantum -particle, which is currently being continued as On BV-Quantization.
In all modesty, I thought of this as an attempt to do for quantum (field) theory what Lawvere has tried to do for classical continuum mechanics: find its right arrow theory. See for instance his Toposes of Laws of Motion which we once discussed a bit here.
Like the principle of general covariance which guided Einstein in the formulation of the classical theory of gravity, the principle of general tovariance becomes rather tautologous after becoming accustomed to it: I think the fact that these ideas once were held as “principles” will in the future just be taken as indication that one had been terribly confused before “discovering” the principle.
Of course the recent ideas by Andreas Döring and Chris Isham on understanding the noncommutativity of the quantum phase space as the result of being internal to a certain topos, which we talked about quite a bit here (I, II, III, IV, V) enters Landsmann’s discussion prominently.
Isham and Döring seem to have seriously sparked new interest in the idea of internalized physics. I wish I could attend the workshop on Categories, Logic and Physics in London next January.
December 3, 2007
Look Around You
Posted by John Baez
The Catsters have finally got some serious competition on the math video front. Check out this gem, brought to the Café’s attention by Allan Erskine:
But before you do, set your calculator to maths!
An Unlikely Result
Posted by John Baez
Andrew Stacey points out this weekend’s most amusing submission to the arXiv:
- A.N. Other, An unlikely result.
Believe it or not, this is not the first paper by this author with this title.
You can poke around and figure out for yourself what’s going on…
December 1, 2007
Astronomers Destroy Universe
Posted by John Baez
On November 12th, Lawrence Krauss and James Dent wrote a paper that caused quite a kerfuffle in the media:
- Lawrence Krauss and James Dent, The late time behavior of false vacuum decay: possible implications for cosmology and metastable inflating states (version 1).
Most of the paper is quite technical, but on November 22, the New Scientist took a couple of sentences and blew them out of proportion in a story with a far-out title: Has observing the universe hastened its end?
On November 24, Krauss and Dent changed those sentences to something a bit more reasonable.
The bulk of the paper remains unchanged… but nobody ever talked about that part. It’s a cute example of how sensationalism amplifies the least reliable aspects of science, while ignoring the solid stuff.
Details follow…
 Posts with this logo use
Posts with this logo use 














