January 26, 2012
Banning Elsevier
Posted by John Baez
Please take the pledge not to do business with Elsevier. 402 scientists have done it so far:
You can separately say you 1) won’t publish with them, 2) won’t referee for them, and/or 3) won’t do editorial work. At least do number 2): activism is rarely so little work, but when a huge corporation relies so heavily on nasty monopolistic practices and unpaid volunteer labor, they leave themselves open to this.
January 21, 2012
Multiple M5-branes, String 2-connections, and 7d nonabelian Chern-Simons theory
Posted by Urs Schreiber
We are in the process of finalizing a little article:
Domenico Fiorenza, Hisham Sati, Urs Schreiber,
Multiple M5-branes, String 2-connections, and 7d nonabelian Chern-Simons theory
Below is the abstract, and, below the fold, the beginning of the introduction. A pdf with the current version is behind the above link.
We would be grateful for comments.
The article is written in a non-formal style with an audience of certain physicists in mind, but ample pointers are given to places where all the ingredients are spelled out in detail and precisely.
Abstract
The worldvolume theory of coincident M5-branes is expected to contain a nonabelian 2-form/nonabelian gerbe gauge theory that is a higher analog of self-dual Yang-Mills theory. But the precise details – in particular the global moduli / instanton / magnetic charge structure – have remained elusive.
Here we argue that the holographic dual of this nonabelian 2-form field, under duality, can be deduced from anomaly cancellation.
We find this way a 7-dimensional nonabelian Chern-Simons theory of twisted String 2-connection fields, which, in a certain higher gauge, are given locally by non-abelian 2-forms with values in a Kac-Moody loop Lie algebra. We construct the corresponding action functional on the entire smooth moduli 2-stack of field configurations, thereby defining the theory globally, at all levels and with the full instanton structure, which is nontrivial due to the twists imposed by the quantum corrections. Along the way we explain some general phenomena of higher nonabelian gauge theory that we need.
January 15, 2012
Vorsicht! Funktor!
Posted by Tom Leinster
Constanze Roitzheim pointed me to this excellent photo by Gerd Laures:
Translation: Caution! Functor! Keep 2m back.
Click the photo for the full size version.
January 13, 2012
Logic as Invariant-Theory
Posted by David Corfield
Greetings from Oberwolfach, where I’m attending a workshop on Explicit Versus Tacit Knowledge in Mathematics. ‘Tacit knowledge’ is a term we owe to Michael Polanyi, though we haven’t heard all that much about his views this week. (In fact, the attentive Café visitor may have seen more of Polanyi here over the years, here, here and here.)
But there are always plenty of reasons to hope to gain from a workshop, and I was particularly interested by a talk by Christophe Eckes on the debt Hermann Weyl owed to Felix Klein and his group-theoretic approach. I was already alerted to the theme earlier in the week, having found out about a paper An Extension of Klein’s Erlanger Program: Logic as Invariant-Theory in which F. I. Mautner had attempted to carry over Weyl’s treatment of the Erlanger Program from Classical Groups to logic. Essentially we’re seeing the action of the symmetric group, , on, a set of elements and on powers of . Invariants of the full symmetric group are logical constructions. We even get to see a tensor notation in whose terms propositions may be expressed.
January 12, 2012
Propositions as Some Types and Algebraic Nonalgebraicity
Posted by Mike Shulman
Perhaps the aspect of homotopy type theory which causes the most confusion for newcomers (at least, those without a background in type theory) is its treatment of logic. With that in mind, I want to share some general thoughts about all the ways in which foundational systems can treat logic, and why I think HoTT makes the choice that it does. This even turns out to have interesting implications for the difference between “algebraic” and “non-algebraic” structures.
January 11, 2012
Mathematical Aspects of String and M-Theory in Cambridge
Posted by Urs Schreiber
The workshop Mathematical Aspects of String and M-theory is currently is taking place in Cambridge, in the context of the program Mathematics and Applications of Branes in String and M-theory.
I am not there (I am at Higher structures along the lower Rhine), but my co-author Hisham Sati is. Hisham is speaking about our upcoming article with Domenico Fiorenza, on the 7-dimensional Chern-Simons QFT of String 2-connections dual to M5-branes. That’s the one I had briefly mentioned in my talk in Göttingen a few weeks back. A nice application of higher cohesive topos theory, I think.
While, judging from the workshop abstracts, this seems the only higher category theory that is explicitly mentioned in Oxford, of course there is secretly higher category theory all over the place in this subject. For instance the two talks on generalized complex geometry are secretly about the geometry of Courant Lie 2-algebroids.
I’ll post more details a little later.
January 3, 2012
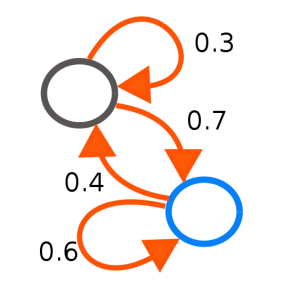
A Semigroup Approach to Finite Markov Chains
Posted by Tom Leinster
Guest post by Benjamin Steinberg
A finite Markov chain is a very simple kind of transition system:
It can be encoded as a square matrix of nonnegative reals, each of whose rows sums to 1 (a ‘stochastic matrix’). Here you’ll meet the fundamental results on finite Markov chains, proved in a way that appears to be new. — TL
I’m going to prove all the standard finite Markov chain convergence results using the theory of compact semigroups. This approach may be known, but I couldn’t find it. I don’t obtain any of the bounds on convergence, although I suppose one can obtain them via this method with a little work.
 Posts with this logo use
Posts with this logo use