Posts with this logo use 
August 31, 2007
Axis of Evil? Or Axis of Opportunity?
Posted by John Baez
This paper argues that the axes of elliptical galaxies don’t point in random directions. but have a slight tendency to point roughly towards the ‘axis of evil’. The ‘axis of evil’ is a controversial concept in itself: a direction that seems to be picked out by anisotropies in the cosmic microwave background!
Trying to put a more positive spin on the idea, the author calls it the ‘axis of opportunity’:
- Michael J. Longo, The axis of opportunity: the large-scale correlation of elliptical galaxies.
I thank Daniel Rocha for pointing out this paper to me.
August 30, 2007
On Hess and Lack on Bundles of Categories
Posted by Urs Schreiber
Kathryn Hess and Steve Lack are working on a Bundle Theory for Categories, various aspects of which are very close to the things we like to talk about here at the -Café.
John Baez kindly pointed out to me the very nice set of slides
Kathryn Hess
Bundle Theory for Categories
(slides) .
These slides discuss definitions and examples of this framework from 0-categories over 1-categories to 2-categories.
Here I shall walk through the material of that talk concerning 1-categories by exemplifying every step in terms of the example where the bundle of categories in question is the Atiyah groupoid of an (ordinary!) principal -bundle.
I believe this is helpful for putting these constructions in perspective.
I shall make use of the discussion of the Atiyah groupoid as given in
-Transport and Higher Schreier Theory
and
Curvature, the Atiyah Sequence and Inner Automorphisms,
but I try to make the discussion self-contained and elementary.
Question about von Neumann Algebras
Posted by Urs Schreiber
Jim Stasheff asks me to share this quote:
Study is hard work. It is so much easier to find something else to do in its place than to stay at the grind of it. We have excuses aplenty for avoiding the dull, hard, daily attempt to learn. There is always something so much more important to do than reading. There is always some excuse for not stretching our souls with new ideas and insights now or yet or ever.
by Joan Chittister
Quoted in Essential Monastic Wisdom, by Hugh Feiss .
And another email I receive reminds me of the truth of this. Somebody writes
In one of your entries in the -category Café blog, you raised a question that is very relevant to what I’m doing. Did you settle the question in the end as to whether all bimodules over von Neumann algebras really do for sure come from homomorphisms? Do you have any suggestions for what I can read to find out?
This reminds me of my feeble attempts to learn von Neumann algebra theory (was it here?), and how I already start forgetting what I did learn. I think the above statement, that all bimodules in fact come from algebra homomorphisms, is at least true for type III factors.
Somebody please help. Me, and, probably more importantly, the person who wrote the above message.
August 29, 2007
Journal Publishers Hire the “Pit Bull of PR”
Posted by John Baez
Ever hear about PRISM? It’s a publisher’s group — backed by Elsevier and others — that’s leading the fight against open access to scholarly publications.
To plan their strategy, PRISM hired none other than Eric Dezenhall:
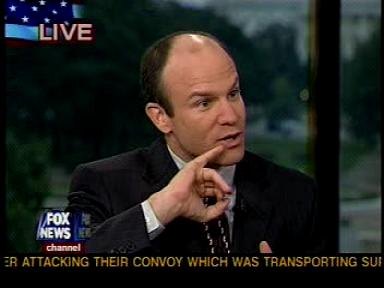
This is the guy who BusinessWeek called the “pit bull of PR”. The guy whose firm Bill Moyers called “the Mafia of industry”. The guy who wrote:
Damage control used to be about soft, fuzzy concepts like image. Now it’s about survival, and this has made the battle bloodier.
And, guess what he advised the publishers to do!
August 28, 2007
Arrow-Theoretic Differential Theory III: Higher Morphisms
Posted by Urs Schreiber
In Arrow-Theoretic Differential Theory, Part II I argued that we need to pass to tangent categories in order to understand, not just -curvature, but also higher morphisms of Lie -algebras.
In Vienna John Baez quizzed me about these ideas, thereby leading me to the more refined insight which I mentioned in More on Tangent Categories.
This insight, which involved making explicit a fact and a construction which I had already been using in a way but not truly realized myself, I have now started to seriously incorporate while revising the provisional Structure of Lie -algebras.
Since it all seems to work out quite nicely – unless I am making some dumb mistake – here is an update on that matter:
Higher Morphisms of Lie -Algebras from Arrow-Theoretic Differential Theory
Abstract.
We would like to achieve a good explicit understanding of higher morphisms of Lie -algebras. We notice that various formerly puzzling aspects of this seem to become clearer as one passes from Lie -algebras to their Lie -algebras of inner derivations in a certain way. Using this, we define higher morphisms of Lie -algebras explicitly and in general. These should constitute an -category. While we fall short of verifying this in full generality, we do obtain the Baez-Crans 2-category of Lie 2-algebras [1] in the special case where we restrict everything to Lie 2-algebras.
August 27, 2007
This Week’s Finds in Mathematical Physics (Week 256)
Posted by John Baez
In week256, learn a bit of what happened at a conference on Poisson sigma models and Lie algebroids at the Erwin Schrödinger Institute, run by Anton Alekseev, Henrique Bursztyn and Thomas Strobl. Higher categories are finding their way into classical mechanics! Then, hear more of the Tale of Groupoidification: how to turn a span of groupoids into an operator between vector spaces.
August 26, 2007
The Reasoner
Posted by David Corfield
My past and future colleague Jon Williamson started a monthly digest of research on reasoning - The Reasoner. I was asked to guest edit the August edition, which required me to write an editorial and to interview someone of my choice. I opted for Brendan Larvor, a philosopher with very close interests to my own. You can read these items here.
August 25, 2007
The G and the B
Posted by Urs Schreiber
We have a pretty good understanding of what the “-field” in string theory really is, in terms of arrow-theory.
This nicely explains a bunch of things. I used to be very annoyed with myself, though, for not understanding, on this nice abstract level, one of the more intriguing aspects of the -field:
beyond its mere nature as being the 2-categorical version of a line bundle with connection, it turns out that the connection 2-form here unifies in an intriguing way with a Riemannian metric (and with a dilaton field, in fact).
Both these rank-2 tensors and sum up to an object which is known as the “open string metric” to string theorists, and which happens to have a surprisingly nice and natural geometrical interpretation in the context of what is called generalized complex geometry.
In this approach, due to Nigel Hitchin, one studies the geometry of manifolds all in terms of the sum of their tangent and cotangent bundle making use of various kinds of useful natural structures present on this bundle, like its canonical bilinear pairing as well as the Courant bracket.
As is indicated to some extent in section 3.8 of
Marco Gualtieri
Generalized Complex Geometry
math.DG/0401221
this bundle is to be thought of as the Atiyah Lie 2-algebroid of an abelian gerbe on , hence as the infinitesimal version of something like the 2-groupoid of automorphisms of the corresponding 2-bundle.
The more or less obvious -algebroid structures on should corespond to the Atiyah Lie -algebroids of --bundles.
While I do follow all the algebra underlying generalized complex geometry, I had always said to myself that at some point I should better understand what all this really means. Given the available nice categorical picture of line 2-bundles, there should be a nice arrow-theoretic integrated version of understanding all this, showing how a line 2-bundle with connection knows something about Riemannian structures.
Unfortunately, I had never really taken the time to think this through.
Now, today Marco Gualtieri approached me with a question. Since he is already happy with having unified the 2-form connection with the Riemannian metric in his formalism, he was trying to get hints for how all the other string background fields would fit into this mathematical picture, like the RR-forms and in particular the dilaton.
This made me really angry with myself. I wished I had figured out at least some of the answers to these obviously open and crucial questions before he asked me! I knew these needed to be answered at some point.
As it goes, this kind of frustration sometimes is the best motivatin to get going. While S. Merkulov was teaching us this morning about operads, Poisson structures and graph complexes, I believe I made some progress with understanding what’s going on.
The key is, it seems, to first figure out what the Atiyah -groupoid of an -bundle really is. I’ll discuss this using tangent -categories and flows on -categories, as described in Arrow-theoretic differential geometry.
I shall try to indicate what I mean by that, and how it gives rise to the appearance of the structures we see in generalized complex geometry.
August 24, 2007
That Shift in Dimension
Posted by Urs Schreiber
John Baez and I spent the evening in Café Einstein in Vienna (remember, we are at that conference), drinking beer and talking about Stokes’ theorem, natural -transformations and the holographic principle, and how it is all the same thing, really.
Well, okay, I admit we didn’t quite finish proving that theorem, or even making that statement precise. But we had those printouts with us, and after sufficiently many beers, we very much enjoyed figuring out some simple underlying principle of the – at first sight apparently mind bogglingly weird – statement of
Maxim Kontsevich
Deformation quantization of Poisson manifolds, I
q-alg/9709040,
which says that any classical kinematics is canonically quantizable by some strange formula which involves lots of sums over lots of diagrams…
…and the maybe even more surprising explanation of this formula (which Kontsevich apparently knew but didn’t bother to talk about) in terms of correlators of a topological two-dimensional theory of quantum fields with values in the original phase space (hence something that is everywhere of one dimension higher than one would think it should be) as given in
Alberto S. Cattaneo, Giovanni Felder
A path integral approach to the Kontsevich quantization formula
math/9902090 .
John went to bed, while I carefully carried our little insight back to the institute, in my bare hands, so as to talk about it here. The following is supposed to, in turn, help explain, in elementary terms understandable by anyone who understands all or either of
- high school quantum mechanics
- Stokes’ theorem
why on earth the quantization of an -dimensional theory may be obtained by a topological -dimensional field theory.
This is meant for those who enjoy things like Kindergarten Quantum Mechanics. If you are not among these, don’t bother continue reading.
August 23, 2007
Wilson Loop Defects on the String
Posted by Urs Schreiber
Just heard a very interesting talk by Samuel Monnier on his work
A. Alekseev, S. Monnier
Quantization of Wilson Loops in Wess Zumino Witten models
hep-th/0702174 .
August 22, 2007
Lyakhovich and Sharapov on QFT (On BV-Quantization, Part III)
Posted by Urs Schreiber
Today at ESI in Vienna, S. Lyakhovich kindly pointed me to lots of his work. While most everybody was gone hiking, I spent the afternoon reading his articles.
These all develop two main threads:
A) A very clear-sighted description of classical and quantum, Lagrangian and Hamiltonian, gauge and constrained mechanics, closely related to, but going beyond, BV-formalism. Lyakhovich gives the nicest description of the BRST operator which I remember having seen.
B) Holography. While Lyakhovich doesn’t mention that word, he does discuss the underlying issues. In particular, this work does provide some nice insights into the relation between Chern-Simons theory in -dimensions and the coresponding theories on the -dimensional boundary.
I’d expect that various aspects of this body of work will give the impression of familiarity to various experts. But I am struck by the clarity with wich these concepts are understood and ordered to a coherent whole.
Among the many talks we had related to BV-AKSZ and holographic phenomena, all apparently pointing to a deeper story waiting at our fingertips to be fully unraveled, the one on this work stands out as having the clear intent not only to plough through labyrinths of impressive formulas, but to actually increase the level of conceptual understanding.
Gerbes in The Guardian
Posted by John Baez
In his post on Future Gazing, David Corfield invites us to predict the future of -categories over the next year — the second year of the n-Café. I’m seeing lots of signs that -categories are catching on — but it could be happening even faster than I expected. Here’s one article I would not have thought to see in an important British newspaper:
- Marc Abraham, Beyond definition: when I say gerbe I don’t mean grebe, The Guardian, Education Guardian Weekly, August 21, 2007.
Thanks go to Eugenia Cheng for pointing this one out!