The n-Category Café

Let $P_1(X)$ be the groupoid of thin homotopy classes of paths and${\Pi }_1(X)$ is the fundamental groupoid.

Then we have a short exact sequence of path groupoids $${\Omega }_1(X)\to P_1(X)\to {\Pi }_1(X).$$ ${\Omega }_1(X)$ is the groupoid of closed paths (loops).

On the other hand, the integrated Atiyah sequence of the principal bundle $P$ is the short exact sequence $$\mathrm{Ad}P\to P{\times }_{G}P\to {\Pi }_1(X).$$ (Here I am for simplicitly assuming that $X$ is simply connected, so that ${\Pi }_1(X)$ is the codiscrete grupoid over $X$. If $X$ is not simply connected there is a relatively straightforward generalization of everything in sight.)

For any connection on $P$, its parallel transport is a functor $$\mathrm{tra}:P_1(X)\to P{\times }_{G}P\hookrightarrow G\mathrm{Tor}.$$

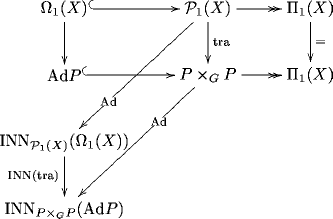
This extends to a morphism of exact sequences of groupoids

$$ (A)

One crucial point is that the groupoids in the middle of the sequences act by conjugation – hence by “inner” automorphisms – on those on the left.

This allows us to turn the parallel transport 1-functor $\mathrm{tra}$ into a functor $$\mathrm{Ad}\circ \mathrm{tra}:P_1(X)\to {\mathrm{INN}}_{P{\times }_{G}P}(\mathrm{Ad}P).$$ This functor tells us how the monodromy groups of the original functor get transformed as we conjugate loops by paths.

The 2-groupoid ${\mathrm{INN}}_{P{\times }_{G}P}(\mathrm{Ad}P)$ is codiscrete at top level (all its Hom-categories are codiscrete). This is the 2-groupoid that the curvature 2-functor of $\mathrm{tra}$ takes values in. Codiscreteness of ${\mathrm{INN}}_{P{\times }_{G}P}(\mathrm{Ad}P)$ then induces the Bianchi identity on curvature.

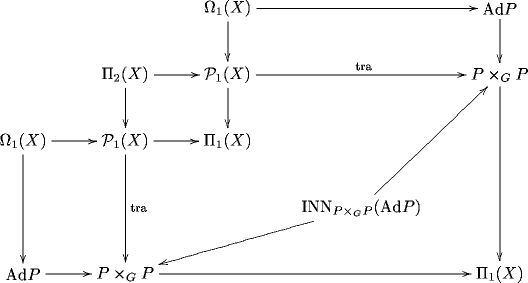
To see this – and that’s the point of this discussion here – we pull back the sequences (A) along themselves to obtain

Here the fundamental 2-groupoid ${\Pi }_2(X)$ appears in its incarnation where 1-morphisms are taken to be thin homotopy classes of paths. (And now I am even assuming that $X$ is 2-connected, for simplicity. Otherwise there is a more or less obvious way to adapt the entire construction.)

Then the two nested pullbacks give us a unique canonical factorization morphism. That’s our curvature 2-functor

So by regarding the connection as a morphism from the path sequence of the base to the Atiyah sequence of the bundle, also the discussion of curvature becomes a little more compelling.

More details in the above mentioned notes.