Entropy and Diversity Is Out!
Posted by Tom Leinster
My new book, Entropy and Diversity: The Axiomatic Approach, is in the shops!
If you live in a place where browsing the shelves of an academic bookshop is possible, maybe you’ll find it there. If not, you can order the paperback or hardback from CUP. And you can always find it on the arXiv.
I posted here when the book went up on the arXiv. It actually appeared in the shops a couple of months ago, but at the time all the bookshops here were closed by law and my feelings of celebration were dampened.
But today someone asked a question on MathOverflow that prompted me to write some stuff about the book and feel good about it again, so I’m going to share a version of that answer here. It was long for MathOverflow, but it’s shortish for a blog post.
There are lots of aspects of the book that I’m not going to write about here. My previous post summarizes the contents, and the book itself is quite discursive. Today, I’m just going to stick to that MathOverflow question (by Aidan Rocke) and what I answered.
Briefly put, the question asked:
Might there be a natural geometric interpretation of the exponential of entropy?
I answered more or less as follows.

The direct answer to your literal question is that I don’t know of a compelling geometric interpretation of the exponential of entropy. But the spirit of your question is more open, so I’ll explain (1) a non-geometric interpretation of the exponential of entropy, and (2) a geometric interpretation of the exponential of maximum entropy.
Diversity as the exponential of entropy
The exponential of entropy (Shannon entropy, or more generally Rényi entropy) has long been used by ecologists to quantify biological diversity. One takes a community with species and writes for their relative abundances, so that . Then , the exponential of the Rényi entropy of of order , is a measure of the diversity of the community, or the “effective number of species” in the community.
Ecologists call the Hill number of order , after the ecologist Mark Hill, who introduced them in 1973 (acknowledging the prior work of Rényi). There is a precise mathematical sense in which the Hill numbers are the only well-behaved measures of diversity, at least if one is modelling an ecological community in this crude way. That’s Theorem 7.4.3 of my book. I won’t talk about that here.
Explicitly, for ,
(). The two exceptional cases are defined by taking limits in , which gives
(the exponential of Shannon entropy) and
Rather than picking one to work with, it’s best to consider all of them. So, given an ecological community and its abundance distribution , we graph against .
This is called the diversity profile of the community, and is quite informative. Different values of the parameter tell you different things about the community. Specifically, low values of pay close attention to rare species, and high values of ignore them.
For example, here’s the diversity profile for the global community of great apes:
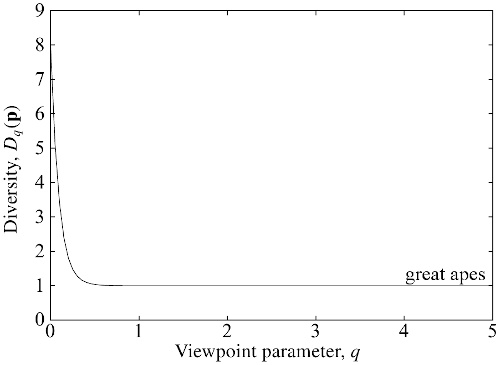
(from Figure 4.3 of my book). What does it tell us? At least two things:
The value at is , because there are species of great ape present on Earth. measures only presence or absence, so that a nearly extinct species contributes as much as a common one.
The graph drops very quickly to — or rather, imperceptibly more than . This is because 99.9% of ape individuals are of a single species (humans, of course: we “outcompeted” the rest, to put it diplomatically). It’s only the very smallest values of that are affected by extremely rare species. Non-small s barely notice such rare species, so from their point of view, there is essentially only species. That’s why for most .
Maximum diversity as a geometric invariant
A major drawback of the Hill numbers is that they pay no attention to how similar or dissimilar the species may be. “Diversity” should depend on the degree of variation between the species, not just their abundances. Christina Cobbold and I found a natural generalization of the Hill numbers that factors this in — similarity-sensitive diversity measures.
I won’t give the definition (see that last link or Chapter 6 of the book), but mathematically, this is basically a definition of the entropy or diversity of a probability distribution on a metric space. (As before, entropy is the log of diversity.) When all the distances are , it reduces to the Rényi entropies/Hill numbers.
And there’s some serious geometric content here.
Let’s think about maximum diversity. Given a list of species of known similarities to one another — or mathematically, given a metric space — one can ask what the maximum possible value of the diversity is, maximizing over all possible species distributions . In other words, what’s the value of
where now denotes the similarity-sensitive (or metric-sensitive) diversity? Diversity is not usually maximized by the uniform distribution (e.g. see Example 6.3.1 in the book), so the question is not trivial.
In principle, the answer depends on . But magically, it doesn’t! Mark Meckes and I proved this. So the maximum diversity
is a well-defined real invariant of finite metric spaces , independent of the choice of .
All this can be extended to compact metric spaces, as Emily Roff and I showed. So every compact metric space has a maximum diversity, which is a nonnegative real number.
What on earth is this invariant? There’s a lot we don’t yet know, but we do know that maximum diversity is closely related to some classical geometric invariants.
For instance, when is compact,
where is the volume of the unit -ball and is scaled by a factor of . This is Proposition 9.7 of my paper with Roff and follows from work of Juan Antonio Barceló and Tony Carbery. In short: maximum diversity determines volume.
Another example: Mark Meckes showed that the Minkowski dimension of a compact space is given by
(Theorem 7.1 here). So, maximum diversity determines Minkowski dimension too.
There’s much more to say about the geometric aspects of maximum diversity. Maximum diversity is closely related to another recent invariant of metric spaces, magnitude. Mark and I wrote a survey paper on the more geometric and analytic aspects of magnitude, and you can find more on all this in Chapter 6 of my book.
Postscript
Although diversity is closely related to entropy, the diversity viewpoint really opens up new mathematical questions that you don’t see from a purely information-theoretic standpoint. The mathematics of diversity is a rich, fertile and underexplored area, beckoning us to come and investigate.




Re: Entropy and Diversity Is Out!
The exponential of
is
and last week David Jaz-Myers told me a nice categorification of this quantity. Suppose is any function between sets. Let be the fiber over :
We can think of as a ‘set over ’, and in the category of sets over we have
In other words, this is the set of functions from to itself that preserve every fiber.
David told me that someone had just come out with a paper using this idea to think about entropy in new ways. I can’t remember who that was, but maybe someone can tell us.