Extraordinary 2-Multicategories
Posted by Mike Shulman
Let’s take a break from all this type theory and -stuff and do some good old 2-dimensional category theory. Although as usual, I want to convince you that plain old 2-categories aren’t good enough, and we need something different. But as far as I know, the structure I have in mind today doesn’t exist yet! I think I know how to define it, but before I go to the trouble, I want to know what people think about it, and whether anyone has seen anything like it before. So I’ll just describe informally what I think this structure should look like.
Briefly, what I want is a “minimal” extension of a 2-category which can also include extraordinary natural transformations.
So what are extraordinary natural transformations (a.k.a. “extranatural” transformations)? The nlab page about them is fairly nice, and John also wrote a comment here about why you might want them. Namely, if is a closed monoidal category, then its internal-hom is a functor , and it comes with “evaluation” and “coevaluation” maps that look like the counit and unit of an adjunction. These are natural in , and for fixed they are the unit and counit of an adjunction, but we’d like to say that they’re “natural in ” as well. That doesn’t make sense for the usual kind of “natural,” since appears only on one side of each, but since it appears on that one side twice, once covariantly and once contravariantly, we can define a similar “bent” sort of naturality that does apply. The formal definition can be found here.
Unfortunately, these sorts of transformations aren’t 2-cells in the 2-category , but there must be some kind of 2-category-like structure in which they live. One answer to the question of where they live is a compact closed proarrow equipment. This approach begins by noticing that if are two covariant functors, then an ordinary natural transformation from to can equivalently be defined as a map of profunctors , where is just the hom-functor of , and is defined by . Similarly, if we have a functor and a functor , then a transformation which is natural in and extranatural in can be equivalently defined as to be a map of profunctors , where is the profunctor defined by Thus, if we have a formal notion of “proarrow” for which we can make sense of these constructions, we can define extranatural transformations there.
I’m not going to say any more about that, though, because what I want is something different. Not to say anything against profunctors; as you all know, I love profunctors, and they are useful for all sorts of other things, so this approach puts extranatural transformations into a nice general situation with a nice general calculus. However, if all we want to talk about are extranatural transformations, then going to profunctors introduces a lot of extra baggage, which might not always be present in examples. So I want a structure which generalizes a 2-category just enough to include extranatural transformations.
First, since extranaturality depends on having functors of many variables, it makes sense to use some sort of multicategory. Recall that a multicategory includes morphisms whose domain is a finite list of objects, rather than just a single object, which we write like so: Our multicategories should probably be symmetric, meaning that given any such we can permute the objects in its domain and get another morphism with that permuted domain. Moreover, our multicategories should be -enriched, (i.e. they are “2-multicategories”) so that in addition to having such morphisms, we have 2-cells between two such morphisms . Note that this naive -enrichment only gives us 2-cells between morphisms with the same domain and codomain, which are thus still only “ordinary” natural transformations, although they are now explicitly “natural in many variables.”
Now we can add contravariance, by allowing some of the objects in the domain of a morphism to be decorated with an “op”. For instance, we could have a morphism such as . Composition of such morphisms requires “distributing” contravariance. For example, given such an , if we also have , , and , then we can form the composite . This is just like the usual composition in a multicategory, except that since is “opped” in the domain of , when we plug into we have to distribute the “op” over all the objects in the domain of , turning into . Moreover, when we extend this to the -enrichment by defining the horizontal composite of 2-cells, we have to reverse the direction of any 2-cells whose target is “opped.” For instance, if in the above situation we had another and a 2-cell , then upon composition with we would get a 2-cell in the opposite direction .
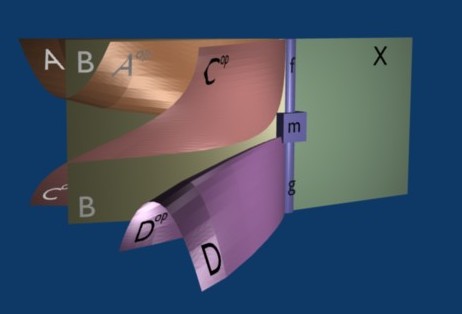
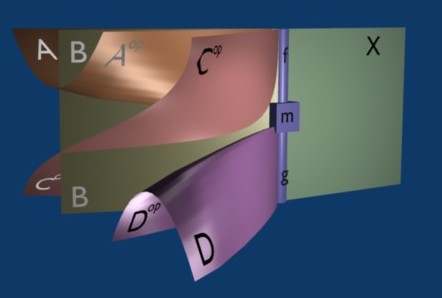
So far, so good, but now what about the extranaturals themselves? These have to be 2-cells between arrows whose domains don’t match up. Or, more precisely, between arrows whose domains aren’t the same, since we do still have to “match up” their domains in some way. Specifically, for an “extranatural 2-cell” from to , each object has to occur either (1) once each in the domains of both and with the same variance, (2) exactly twice in the domain of , once covariantly and once contravariantly, or (3) exactly twice in the domain of , once covariantly and once contravariantly. In fact, we actually need to specify how the objects in the domains are matched up, since if some of them are the same, there might be different ways to do it. For instance, given functors and , there are two kinds of extranatural transformation ; one has components and is natural in and extranatural in , while the other has components and is natural in and extranatural in .
Thus, every “extranatural 2-cell” in our multicategory should come with a “matching” which identifies where the naturality and extranaturality occurs. It’s convenient to draw this matching as a sort of graph. For instance, given and , the graph representing one kind of extranatural 2-cell would look like this:
This graph stipulates that the two copies of in the domain of are matched extranaturally, as are the two copies of in the domain of , while and are matched naturally between the two functors. So our “extraordinary multicategory” will come with a collection of “extranatural 2-cells” between morphisms with possibly-different domains, but each such 2-cell also comes with a graph which matches up the objects in the domains of and in some way. Note that this includes ordinary 2-cells as well: these are just the extranatural ones whose graph is just a series of straight lines.
Now we have to say how to compose such 2-cells. Fortunately, most of the work has been done for us in the original paper that defined extranatural transformations, A generalization of the functorial calculus by Eilenberg and Kelly. There they showed that two extranatural transformations and are composable precisely when, if you paste the graph labeling on top of the graph labeling , you don’t get any closed loops. Moreover, in this case, the resulting transformation is labeled by this composite graph. (If there is a closed loop, then there is a category appearing in the domain of but not in the domains of or , and the “composite” will not be well-defined; it depends on the choice of an object of that category to “compose along”.)
Thus, this tells us exactly how to define “vertical” composition of 2-cells in our multicategory. It’s important to note that just as for extranatural transformations, not every pair of 2-cells with matching source and target will be composable. Finally, the “horizontal” composition should be definable using substitution of graphs; for now I’ll leave that as an exercise.
Let’s call this hypothetical thing an extraordinary 2-multicategory. As far as I know, no one has written down such a thing before, but I would be very glad to find myself wrong. I’m also curious about people’s reaction to such a thing. Does it seem natural or unnatural? Beautiful or ugly? Can it be improved?
The closest thing I know of in the literature is Max Kelly’s theory of clubs. A “club” is a structure kind of like an operad, which can be viewed as a concrete presentation of a monad on ; thus coherence theorems about the algebras for that monad can be stated as theorems about the club. In fact, there are lots of kinds of clubs, and Kelly gave multiple related but not quite equivalent definitions—but one of his definitions is that a club is precisely a generalized operad (in the Leinster-Burroni sense) relative to some cartesian monad on .
The monad parametrizes the “arities” of operations as well as the allowable sorts of “transformations” between operations. If we take the “free symmetric (strict) monoidal category monad,” then clubs over this monad describe structure on categories involving only covariant operations, and natural transformations which can permute variables, but nothing else. The ur-example is, of course, the club for symmetric monoidal categories. Such clubs are almost the same as -enriched symmetric multicategories, so you can think of “the club for symmetric monoidal categories” as almost the same as the free -enriched symmetric multicategory containing a symmetric-monoidal-category object.
Kelly also considered other types of clubs which allow transformations with duplicated variables, but still with only covariant functors, such as the diagonal which appears in the notion of “category with finite products.” He also wanted a version which would describe extranatural transformations, but as far as I can tell, he eventually gave up on this, after realizing that the monad for compact closed categories (which would be describable by such a club, if it existed) is not cartesian, and thus could not be presentable by any such generalized operad in .
I believe there should, however, be a “free extraordinary 2-multicategory containing a compact-closed-category-object,” so that extraordinary 2-multicategories could be used to present 2-theories involving contravariance and extranatural transformations. The reason I think this should work, though Kelly’s approach failed, is the important point I noted above: in an extraordinary 2-multicategory, 2-cells of incompatible graphs cannot be composed, whereas in any sort of club as defined by Kelly, any pair of 2-cells with matching source-target must always be composable. This change does mean that an extraordinary 2-multicategory can no longer be described entirely in , though I think we can describe it in a similar way if we use “partial categories” in which not all composites may exist. That also means it’s not clear whether it can give rise to a monad on , so I’m not sure whether this does anything to solve the actual problem Kelly was trying to address. But regardless, I think the structure should be of interest. Thoughts?

Re: Extraordinary 2-Multicategories
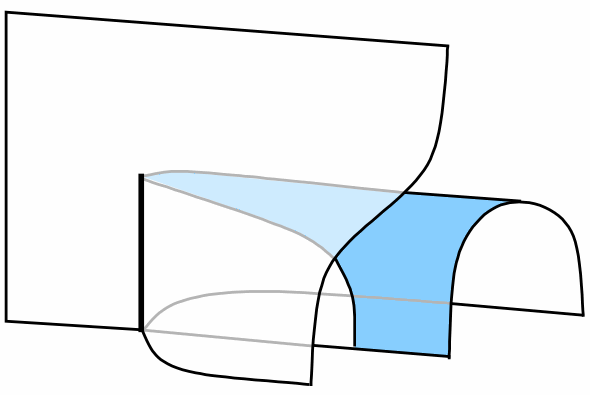
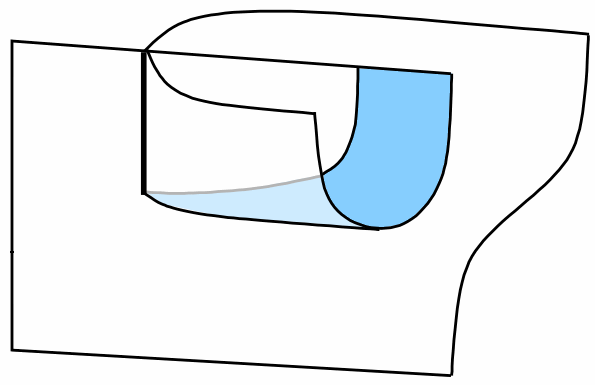
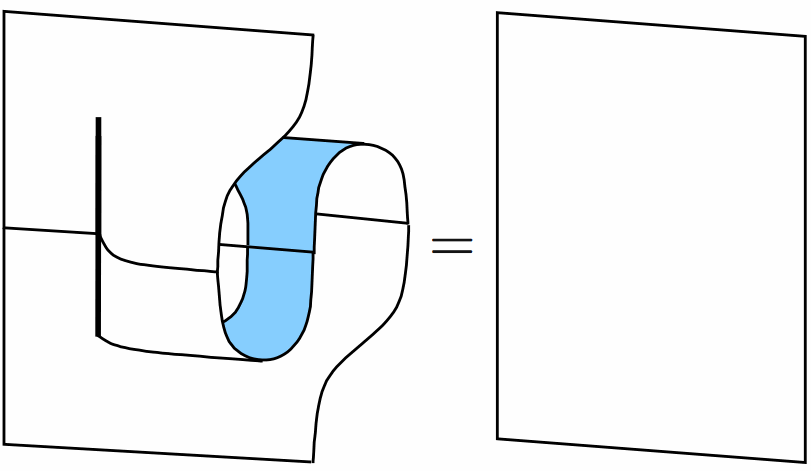
I’ve certainly been thinking about such things recently (such as this week!) – mainly motivated by Hopf monads. So the picture in my last post
is supposed to represent the composition of two extraordinary natural (or dinatural) transformations – you can see the graph as the profile on the right-hand side and the colour blue is supposed to represent the opposite category.
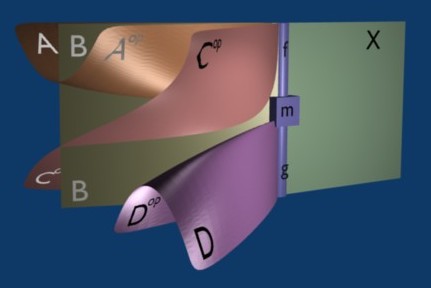
[A very brief explanation of what is going on is as follows. The red line represents a functor , the black line separating the blue and white regions represents a duality functor , and the thick black line represents the triple tensor product (I’m cheating and using coherence here). So the diagram is supposed to represent a transformation from at the bottom to at the top.]
I suspect John will have something to say about this…