The n-Category Café

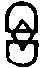
Odd Flow Lines

For any category $C$, it seems to make good sense to address the category of morphism from the fat point $$\mathrm{pt}=\{•\stackrel{\sim }{\to }\circ \}$$ into $C$, which fix the body $(\mathrm{pt}=\{•\})\hookrightarrow \mathrm{pt}$ of the fat point as the categorical tangent bundle $$p:TC\to \mathrm{Obj}(C).$$ The sections of $TC$ form a group, due to the canonical embedding $$\Gamma (TC)\hookrightarrow T_{{\mathrm{Id}}_C}(\mathrm{End}(C)).$$ For $G$ any group, a $G$-flow on $C$ is a group homomorphism $$G\to \Gamma (TC)$$ in this sense.

In particular, if $C=P_1(X)$ is the path groupoid of a smooth space $X$, then smooth $ℝ$-flows $$v:ℝ\to \Gamma (T{P}_1(X))$$ are ordinary vector fields on $X$.

That’s nice, because using this arrow-theoretic differential theory, we now immediately know a vast generalization of the concept of a vector in all kinds of exotic ways.

For instance by replacing $ℝ$ by the finite group ${\mathbb{Z}}_2$. A ${\mathbb{Z}}_2$-flow on $C$ is a group homomorphism $${\mathbb{Z}}_2\to \Gamma (TC).$$ And it might be useful to think of this as a categorical version of an odd vector field. I’ll come to that.

The simplest category with a nontrivial ${\mathbb{Z}}_2$-flow on it is the fat point $$\mathrm{pt}=\{•\stackrel{\sim }{\to }\circ \}$$ itself. Looking at it this way, I am inclinded to call this the categorical superpoint.

Following the authors of the Adinkra-papers (to which I shall come), I will restrict attention to superpoints – but possibly with higher supersymmetry.

Since there is precisely one nontrivial ${\mathbb{Z}}_2$-flow on $\mathrm{pt}$, let’s call it the

$N=1$ superpoint : ${\mathrm{pt}}_{N=1}$

What would be the $N=2$ superpoint, then?

It’s the categorical “wedge” product $${\mathrm{pt}}_{N=2}:={\mathrm{pt}}_{N=1}\otimes {\mathrm{pt}}_{N=1}.$$ I claim. Here “$\otimes$” is the true tensor product on $n$-categories, the one which sends an $n$-category $C_n$ and an $m$-category $D_m$ to the $(n+m)$-category $$C_n\otimes D_m.$$ That’s described in full generality in the beautiful work

Sjoerd Crans
Pasting schemes for the monoidal biclosed structure on $\omega -\mathrm{Cat}$
(ps)

but it is useful to also look at the discussion in

Sjoerd Crans
A tensor product for Gray-categories
(ps).

(I am grateful to Todd Trimble for pointing me to this stuff.)

Notice that, on p. 3, Crans mentions our $N=1$-superpoint under the name $$2_1.$$ What I here call the $(N=2)$-superpoint $${\mathrm{pt}}_{N=2}=\left\{\begin{array}{ccc}(•,•)& \to & (•,\circ )\\ \downarrow & {\Downarrow }^{\sim }& \downarrow \\ (\circ ,•)& \to & (\circ ,\circ )\end{array}\right\}$$ is closely related to what Sjoerd Crans would call $$2_2.$$ And so on.

And indeed, there are precisely two different nondegenerate ${\mathbb{Z}}_2$-flows $${\mathbb{Z}}_2\to T_{{\mathrm{Id}}_{{\mathrm{pt}}_{N=2}}(\mathrm{End}({\mathrm{pt}}_{N=2}))}$$ on the 2-super point.

Adinkras

In

Michael Faux, S. J. Gates Jr
Adinkras: A Graphical Technology for Supersymmetric Representation Theory
hep-th/0408004

the authors argue that it is useful to draw diagrams essentially of the above form for thinking about representations of the 1-dimensional but $N$-extended local super-Poincaré algebra.

This means we need to be thinking in terms of superfields on the line, on which we want to act with the super-Lie algebra whose single even generator is the ordinary derivative $${\partial }_t:\varphi \mapsto \varphi \prime$$ and whose single odd generator $q$ has the graded bracket $$[Q,Q]={\partial }_t.$$

The standard representation of this algebra is spanned by an even field $$\varphi$$ and an odd field $$\psi$$ with the action of $Q$ given by $$\begin{array}{rl}Q\varphi & \propto \psi \\ Q\psi & \propto {\partial }_t\varphi \end{array}.$$

Faux and Gates propose to associate with this representation the diagram $${•}^{\varphi }\to {\circ }^{\psi }$$ (I have switched $•\leftrightarrow \circ$ with respect to their notation) in order to indicate that there are

- two fields in the game (hence two vertices)

- one of which is even (a filled verted)

- and one of which is odd (an open vertex)

- and where the action of $Q$ on one of these involves ${\partial }_t$, while on the other it does not (and this is indicated by the arrow pointing from the latter to the former).

This diagram they call an Adinkra.

Thinking carefully about what superfields really are can prove to be quite tricky. Since it is quite late at night here (but recall, as Blake Stacey notes: maybe a necessary prerequisite for Adinkras to look like categorical diagrams) I won’t try to give a meaningful mathematical exegesis of the above formulas.

Suffice it, for the moment, to notice that not only does the Adinkra $${•}^{\varphi }\to {\circ }^{\psi }$$ look a lot like the $N=1$ superpoint (which a priori might very well be just a coincidence of simple structures), but it also encodes a similar mechanism: an arrow which indicates a transformation that exchanges something with its “odd” partner.

Adrinkas are supposed to become useful as one studies $N$-extended supersymmetry algebras of higher $N$.

In the $N=2$-version of the above setup, we’d have two even fields $${\varphi }_1,{\varphi }_2$$ and two odd fields $${\psi }_1,{\psi }_2$$ and two different odd vector fields $$Q_1,Q_2$$ whose action on ${\varphi }_i$ and ${\psi }_i$ is pretty much as before, but now may also involve swapping the subscript of the fields.

Accordingly, we draw two solid vertices $$\begin{array}{ccc}& & {•}^{{\varphi }_1}\\ \\ \\ \\ & & {•}^{{\varphi }_2}\end{array}$$ and two open ones $$\begin{array}{ccccc}{\circ }^{{\psi }_1}& & & & {\circ }^{{\psi }_2}\end{array}$$ and connect them by arrows going in two perpendicular directions $$\begin{array}{ccc}& & {•}^{{\varphi }_1}\\ & {}^1\swarrow & & {\searrow }^2\\ {\circ }^{{\psi }_1}& & & & {\circ }^{{\psi }_2}\\ & {}_2\searrow & & {\swarrow }_1\\ & & {•}^{{\varphi }_2}\end{array}.$$

There are various ways this swapping of subscripts may be combined with the general susy pattern $q:\varphi \mapsto \propto \psi$ and $q:\psi \mapsto \propto \varphi \prime$. The Adinkra as just drawn, for instance, encodes the transformation behaviour $$\begin{array}{rl}{Q}_1:& {\varphi }_1\mapsto \propto {\psi }_1\\ Q_2:& {\varphi }_1\mapsto \propto {\psi }_2\\ \\ Q_1:& {\psi }_1\mapsto \propto {\partial }_t{\varphi }_1\\ Q_2:& {\psi }_1\mapsto \propto {\varphi }_2\end{array}$$

The theory of representations of $N$-extended $d=1$ supersymmetry, hence also that of these Adinkras, becomes more interesting as one moves to higher $N$.

And I am wondering: maybe, if looked at from the right angle, Adinkras look like categories not just in twilight.

(The Adinkra graphics here are from the site Adinkra Symbols.)