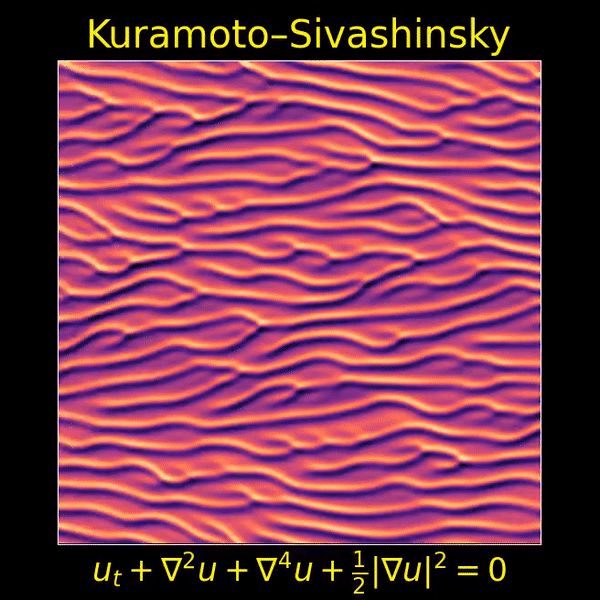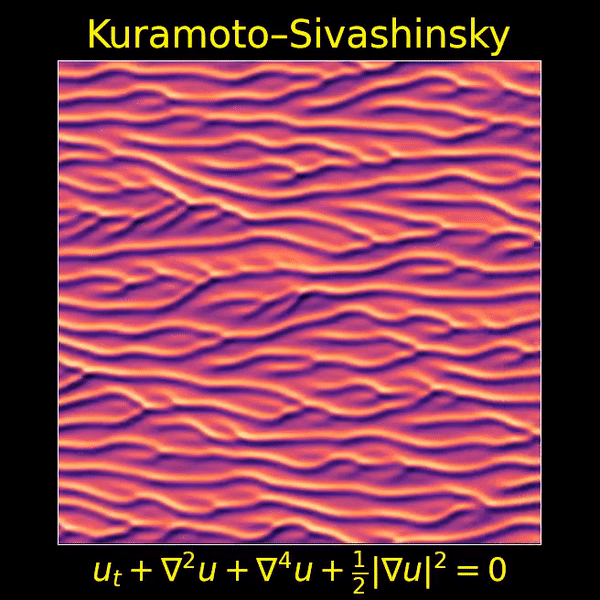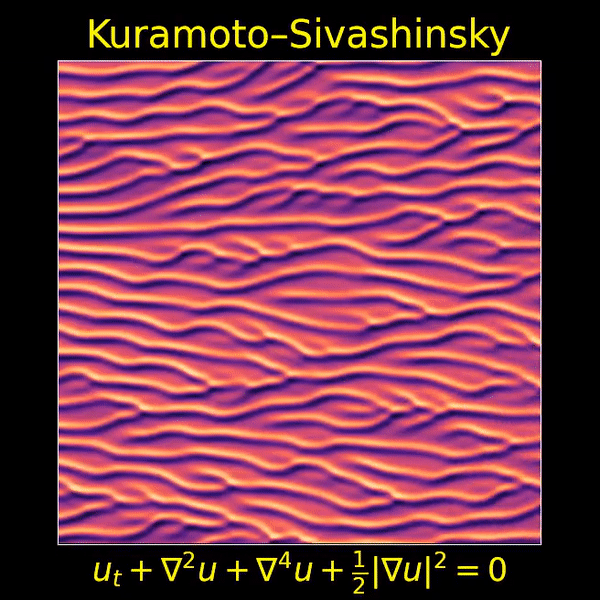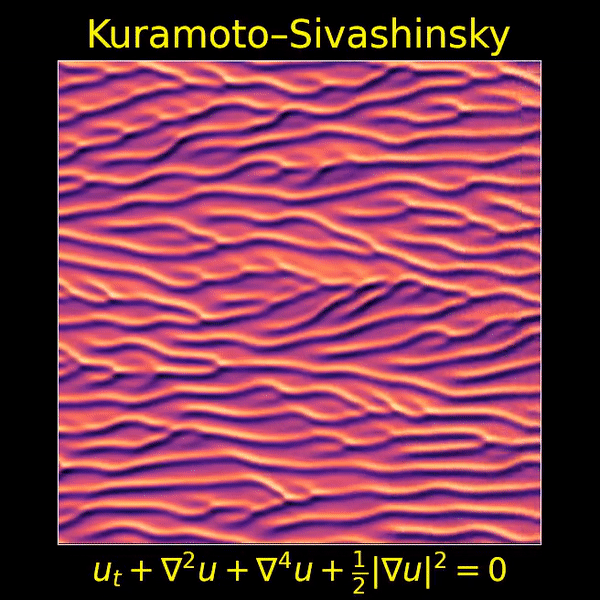October 30, 2021
Firoozbakht’s Conjecture
Posted by John Baez
The Iranian mathematician Farideh Firoozbakht made a strong conjecture in 1982: the th root of the th prime keeps getting smaller as we make bigger! For example:
It’s been checked for all primes up to about 18 quintillion, but nobody has a clue how to prove it. In fact, some experts think it’s probably false.
October 28, 2021
Learn Applied Category Theory!
Posted by John Baez
Do you like the idea of learning applied category theory by working on a project, as part of a team led by an expert? If you’re an early career researcher you can apply to do that now!
- Mathematical Research Community: Applied Category Theory, meeting 2022 May 29–June 4. Details on how to apply: here. Deadline to apply: Tuesday 2022 February 15 at 11:59 Eastern Time.
After working with your team online, you’ll take an all-expenses-paid trip to a conference center in upstate New York for a week in the summer. There will be a pool, bocci, lakes with canoes, woods to hike around in, campfires at night… and also whiteboards, meeting rooms, and coffee available 24 hours a day to power your research!
Later you’ll get invited to the 2023 Joint Mathematics Meetings in Boston.
October 25, 2021
The Kuramoto–Sivashinsky Equation (Part 2)
Posted by John Baez
I love the Kuramoto–Sivashinsky equation, beautifully depicted here by Thien An, because it’s one of the simplest partial differential equations that displays both chaos and a visible ‘arrow of time’. Now we’ll see that it’s also invariant under ‘Galilean transformations’ — that is, transformations into a moving frame of reference.
October 22, 2021
The Kuramoto–Sivashinsky Equation (Part 1)
Posted by John Baez
I love this movie showing a solution of the Kuramoto–Sivashinsky equation, made by Thien An. If you haven’t seen her great math images on Twitter, check them out!
I hadn’t known about this equation, and it looked completely crazy to me at first. But it turns out to be important, because it’s one of the simplest partial differential equations that exhibits chaotic behavior and an ‘arrow of time’: that is, a difference between the future and past.
October 20, 2021
What is the Uniform Distribution?
Posted by Tom Leinster
Today I gave the Statistics and Data Science seminar at Queen Mary University of London, at the kind invitation of Nina Otter. There I explained an idea that arose in work with Emily Roff. It’s an answer to this question:
What is the “canonical” or “uniform” probability distribution on a metric space?
You can see my slides here, and I’ll give a lightning summary of the ideas now.
October 19, 2021
Topos Institute Postdoc
Posted by John Baez
The Topos Institute is trying to hire a postdoc to work on polynomial functors! Here is the ad, written by David Spivak.
October 15, 2021
Dynamics of Reason Revisited
Posted by David Corfield
A couple of years ago, I mentioned a talk reporting my latest thoughts on a very long-term project to bring Michael Friedman’s Dynamics of Reason (2001) into relation with developments in higher category theory and its applications.
While that Vienna talk entered into some technicalities on cohomology, last week I had the opportunity of speaking at our departmental seminar in Kent, and so thought I’d sketch what might be of broader philosophical interest about the project.
You can find the slides here.
October 4, 2021
Stirling’s Formula
Posted by John Baez
Stirling’s formula says
where means that the ratio of the two quantities goes to as
Where does this formula come from? In particular, how does the number get involved? Where is the circle here?
 Posts with this logo use
Posts with this logo use