March 31, 2020
Structured Cospans and Double Categories
Posted by John Baez
This talk on structured cospans and double categories is the first of a two-part series; the second part is about structured cospans and Petri nets.
I gave this first talk at the ACT@UCR seminar. You can see the slides here, or download a video here, or watch the video on YouTube.
Afterwards we had discussions at the Category Theory Community Server, and you can see those here:
https://categorytheory.zulipchat.com/
(To join this, click here. This link will expire in a while.)
March 30, 2020
Online Worldwide Seminar on Logic and Semantics
Posted by John Baez
Someone should make a grand calendar, readable by everyone, of all the new math seminars that are springing into existence. Here’s another:
- Online Worldwide Seminar on Logic and Semantics, organized by Alexandra Silva, Pawel Sobocinski and Jamie Vicary.
There will be talks fortnightly at 1 pm UTC, which is currently 2 pm British Time, thanks to daylight savings time. Here are the first few:
Wednesday, April 1, — Kevin Buzzard, Imperial College London: “Is HoTT the way to do mathematics?”
Wednesday, April 15 — Joost-Pieter Katoen, Aachen University: “Termination of probabilistic programs”.
Wednesday, April 29 — Daniela Petrisan, University of Paris: “Combining probabilistic and non-deterministic choice via weak distributive laws”.
Wednesday, May 13 — Bartek Klin, Warsaw University: “Monadic monadic second order logic”.
Wednesday, May 27 — Dexter Kozen, Cornell University: “Brzozowski derivatives as distributive laws”.
March 28, 2020
Pyknoticity versus Cohesiveness
Posted by David Corfield
Back to modal HoTT. If what was considered last time were all, one would wonder what the fuss was about. Now, there’s much that needs to be said about type dependency, types as propositions, sets, groupoids, and so on, but let me skip to the end of my book to mention modal types, and in particular the intriguing use of modalities to present spatial notions of cohesiveness. Cohesion is an idea, originally due to Lawvere, which sets out from an adjoint triple of modalities arising in turn from an adjoint quadruple between toposes of spaces and sets of the kind:
components discrete points codiscrete.
This has been generalised to the -categorical world by Urs and Mike. On top of the original triple of modalites, one can construct further triples first for differential cohesion and then also for supergeometry. With superspaces available in this synthetic fashion it is possible to think about Modern Physics formalized in Modal Homotopy Type Theory. This isn’t just an ‘in principle’ means of expression, but has been instrumental in guiding Urs’s construction with Hisham Sati of a formulation of M-theory – Hypothesis H. Surely it’s quite something that a foundational system could have provided guidance in this way, however the hypothesis turns out. Imagine other notable foundational systems being able to do any such thing.
Mathematics rather than physics is the subject of chapter 5 of my book, where I’m presenting cohesive HoTT as a means to gain some kind of conceptual traction over the vast terrain that is modern geometry. However I’m aware that there are some apparent limitations, problems with ‘-adic’ forms of cohesion, cohesion in algebraic geometry, and so on. In the briefest note (p. 158) I mention the closely related pyknotic and condensed approaches of, respectively, (Barwick and Haine) and (Clausen and Scholze). Since they provide a different category-theoretic perspective on space, I’d like to know more about what’s going on with these.
[Edited to correct the authors and spelling of name. Other edits in response to comments, as noted there.]
March 25, 2020
MIT Categories Seminar
Posted by John Baez
The MIT Categories Seminar is an informal teaching seminar in category theory and its applications, with the occasional research talk. This spring they are meeting online each Thursday, 12 noon to 1pm Eastern Time.
The talks are broadcast over YouTube here, with simultaneous discussion on the Category Theory Community Server. (To join, click here; this link will expire in a while.) Talks are recorded and remain available on the YouTube channel.
Category Theory Community Server
Posted by John Baez

My student Christian Williams has started a community server for category theory, computer science, logic, as well as general science and industry. In just a few days, it has grown into a large and lively place, with people of many backgrounds and interests. Please feel free to join!
Join here:
https://categorytheory.zulipchat.com/join/ia4b73j86j6b5f7kol6qigsv/
(this link will expire in a while) and from then on you can just go here:
http://categorytheory.zulipchat.com
Both the ACT@UCR seminar and the MIT categories seminar will have discussions on this server.
March 24, 2020
ACT@UCR Seminar
Posted by John Baez
Coronavirus is forcing massive changes on the academic ecosystem, and here’s another:
We’re having a seminar on applied category theory at U. C. Riverside, organized by Joe Moeller and Christian Williams.
It will take place on Wednesdays at 5 pm UTC, which is 10 am in California or 1 pm on the east coast of the United States, or 6 pm in England. It will be held online via Zoom, here:
https://ucr.zoom.us/j/607160601
We will have discussions online here:
https://categorytheory.zulipchat.com
To get in, register here:
https://categorytheory.zulipchat.com/join/lc67le0kr6mjr65cgaurj8ot/
(this link will expire in a while), and then look around for “ACT@UCR”.
The first two talks will be:
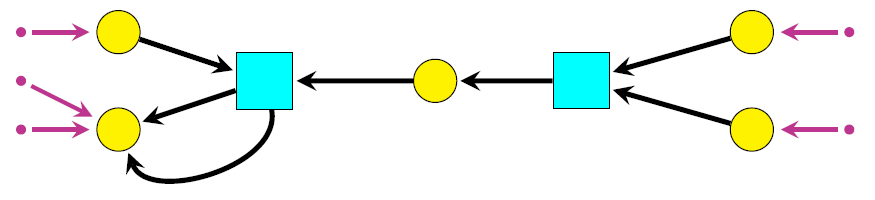
- Wednesday April 1st, John Baez: Structured cospans and double categories.
Abstract. One goal of applied category theory is to better understand networks appearing throughout science and engineering. Here we introduce “structured cospans” as a way to study networks with inputs and outputs. Given a functor , a structured cospan is a diagram in of the form If and have finite colimits and is a left adjoint, we obtain a symmetric monoidal category whose objects are those of and whose morphisms are certain equivalence classes of structured cospans. However, this arises from a more fundamental structure: a symmetric monoidal double category where the horizontal 1-cells are structured cospans, not equivalence classes thereof. We explain the mathematics and illustrate it with an example from chemistry.
- Wednesday April 8th, Prakash Panangaden: A categorical view of conditional expectation.
Abstract. This talk is a fragment from a larger work on approximating Markov processes. I will focus on a functorial definition of conditional expectation without talking about how it was used. We define categories of cones — which are abstract versions of the familiar cones in vector spaces — of measures and related categories cones of functions. We will state a number of dualities and isomorphisms between these categories. Then we will define conditional expectation by exploiting these dualities: it will turn out that we can define conditional expectation with respect to certain morphisms. These generalize the standard notion of conditioning with respect to a sub-sigma algebra. Why did I use the plural? Because it turns out that there are two kinds of conditional expectation, one of which looks like a left adjoint (in the matrix sense not the categorical sense) and the other looks like a right adjoint. I will review concepts like image measure, Radon-Nikodym derivatives and the traditional definition of conditional expectation. This is joint work with Philippe Chaput, Vincent Danos and Gordon Plotkin.
Applied Category Theory 2020 (Part 2)
Posted by John Baez
Due to the coronavirus outbreak, many universities are moving activities online. This is a great opportunity to open up ACT2020 to a broader audience, with speakers from around the world.
The conference will take place July 6-10 online, coordinated by organizers in Boston USA. Each day there will be around six hours of live talks, which will be a bit more spaced out than usual to accommodate the different time zones of our speakers. All the talks will be both live streamed and recorded on YouTube. We will also have chat rooms and video chats in which participants can discuss various themes in applied category theory.
We will give more details as they become available and post updates on our official webpage:
March 19, 2020
Michael Harris on Virtues of Priority
Posted by David Corfield
Michael Harris has an interesting new article on the arXiv today - Virtues of Priority. He wrote it for an edition of a philosophy journal on virtues in mathematics, but, as he explains in the footnote on the first page, it has ended up being published on the arXiv rather than in that journal. I think it provides interested philosophers of mathematics with excellent material to think through issues concerning the role of the virtues in intellectual lives.
Abstract: The conjecture that every elliptic curve with rational coefficients is a so-called modular curve – since 2000 a theorem due in large part to Andrew Wiles and, in complete generality, to Breuil-Conrad-Diamond-Taylor – has been known by various names: Weil Conjecture, Taniyama-Weil Conjecture, Shimura-Taniyama-Weil Conjecture, or Shimura-Taniyama Conjecture, among others. The question of the authorship of this conjecture, one of whose corollaries is Fermat’s Last Theorem, has been the subject of a priority dispute that has often been quite bitter, but the principles behind one attribution or another have (almost) never been made explicit. The author proposes a reading inspired in part by the “virtue ethics” of Alasdair MacIntyre, analyzing each of the attributions as the expression of a specific value, or virtue, appreciated by the community of mathematicians.
March 14, 2020
The Hardest Math Problem
Posted by John Baez
Not about coronavirus… just to cheer you up:
Puzzle. What math problem has taken the longest to be solved? It could be one that’s solved now, or one that’s still unsolved.
Let’s start by looking at one candidate question. Can you square the circle with compass and straightedge? After this question became popular among mathematicians, it took at least 2296 years to answer it!
March 3, 2020
Applied Category Theory 2020 (Part 1)
Posted by John Baez
Here’s the big annual conference on applied category theory:
- ACT2020, 2020 July 6-10, online worldwide. Organized by Brendan Fong and David Spivak.
This happens right after the applied category theory school, which will be held June 29 – July 3. There will also be a tutorial day on Sunday July 5, with talks by Paolo Perrone, Emily Riehl, David Spivak and others.
March 2, 2020
String Diagrams in Computation, Logic, and Physics
Posted by John Baez
A workshop:
- 4th Annual Workshop on String Diagrams in Computation, Logic, and Physics (STRINGS 2020), June 23, 2020, Bergen, Norway.
String diagrams are a powerful tool for reasoning about processes and composition. Originally developed as a convenient notation for the arrows of monoidal and higher categories, they are increasingly used in the formal study of digital circuits, control theory, concurrency, programming languages, quantum and classical computation, natural language, logic and more. String diagrams combine the advantages of formal syntax with intuitive aspects: the graphical nature of terms means that they often reflect the topology of systems under consideration. Moreover, diagrammatic reasoning transforms formal arguments into dynamic, moving images, thus building domain specific intuitions, valuable both for practitioners and pedagogy.
 Posts with this logo use
Posts with this logo use 














