Structured Cospans and Double Categories
Posted by John Baez
This talk on structured cospans and double categories is the first of a two-part series; the second part is about structured cospans and Petri nets.
I gave this first talk at the ACT@UCR seminar. You can see the slides here, or download a video here, or watch the video on YouTube.
Afterwards we had discussions at the Category Theory Community Server, and you can see those here:
https://categorytheory.zulipchat.com/
(To join this, click here. This link will expire in a while.)
Here’s the talk:
Structured cospans and double categories.
Abstract. One goal of applied category theory is to better understand networks appearing throughout science and engineering. Here we introduce “structured cospans” as a way to study networks with inputs and outputs. Given a functor , a structured cospan is a diagram in of the form
If and have finite colimits and is a left adjoint, we obtain a symmetric monoidal category whose objects are those of and whose morphisms are certain equivalence classes of structured cospans. However, this arises from a more fundamental structure: a symmetric monoidal double category where the horizontal 1-cells are structured cospans, not equivalence classes thereof. We explain the mathematics and illustrate it with an example from epidemiology.
This talk is based on work with Kenny Courser and Christina Vasilakopoulou, some of which appears here:
John Baez and Kenny Courser, Structured cospans.
Kenny Courser, Open Systems: a Double Categorical Perspective.
Yesterday Rongmin Lu told me something amazing: structured cospans were already invented in 2007 by José Luiz Fiadeiro and Vincent Schmit. It’s pretty common for simple ideas to be discovered several times. The amazing thing is that these other authors also called them ‘structured cospans’!
- José Luiz Fiadeiro and Vincent Schmitt, Structured co-spans: an algebra of interaction protocols, in International Conference on Algebra and Coalgebra in Computer Science, Springer, Berlin, 2007.
These earlier authors did not do everything we’ve done, so I’m not upset. Their work proves I chose the right name.

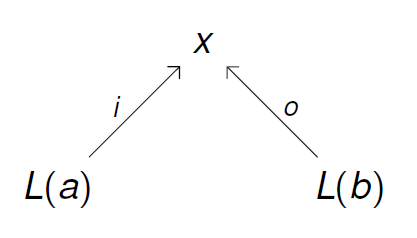
Re: Structured Cospans and Double Categories
The remark
and talk of ‘decoration’ put me in mind of type refinement.
But then if Functors are Type Refinement Systems, refinement should be everywhere.