January 29, 2018
The Stable Homotopy Hypothesis and Categorified Abelian Groups
Posted by Tom Leinster
guest post by Nick Gurski
In December, Niles Johnson, Angélica Osorno, and I posted a proof of the stable homotopy hypothesis in dimension two on the arxiv. This is the fourth paper we have written together on this project (one also joint with Marc Stephan), and since proving the SHH in dimension two was the first step in a long line of research which you might call “an introduction to twice-categorified abelian groups,” I thought now was a good time to try to explain what we have been up to and why.
January 25, 2018
Announcing the 2018 Talbot Workshop: Model-Independent Theory of Infinity-Categories
Posted by Emily Riehl
The Talbot Workshop is a 1-week learning workshop for roughly 35 graduate students and a few postdocs. Most of the talks will be given by participants, and will be expository in nature. This year’s workshop will be held from May 28 - June 2, 2018 at Government Camp, Oregon USA and Dominic Verity and I will be the mentors. The topic is on our joint work developing a theory of -categories from first principles in a model-independent fashion, that is, using a common axiomatic framework that is satisfied by a variety of models. The goal is to demonstrate that theorems proven using the combinatorics of a particular model transfer across specified “change of model” functors. More details about the program, including a preliminary list of talks and references, can be found here.
Applications are now open, and close on Wednesday, February 28 at 11:59PM. You can apply online here.
Talbot is meant to encourage collaboration among young researchers, with an emphasis on graduate students. We also aim to gather participants with a diverse array of knowledge and interests, so applicants need not be an expert in the field– in particular, students at all levels of graduate education are encouraged to apply. As we are committed to promoting diversity in mathematics, we also especially encourage women and minorities to apply.
The Talbot Workshop grant will cover all local expenses including lodging and food and also offer partial funding for participants’ travel costs.
I’m happy to answer questions about the scientific content of this workshop on this blog - please comment below. If you have logistical questions, please do not hesitate to e-mail the organizers at talbotworkshop (at) gmail.com.
On behalf of the organizers: Eva Belmont, Calista Bernard, Inbar Klang, Morgan Opie, Sean Pohorence
More Secrets of the Associahedra
Posted by John Baez
The associahedra are wonderful things discovered by Jim Stasheff around 1963 but even earlier by Dov Tamari in his thesis. They hold the keys to understanding ‘associativity up to coherent homotopy’ in exquisite combinatorial detail.
But do they still hold more secrets? I think so!
January 23, 2018
Statebox: A Universal Language of Distributed Systems
Posted by John Baez
We’re getting a lot of great posts here this week, but I also want to point out this, by one grad students:
- Christian William, Statebox: a universal language of distributed systems, Azimuth, January 22, 2018.
A brief teaser follows, in case you’re wondering what this is about.
FreeTikZ
Posted by Tom Leinster
guest post by Chris Heunen
I don’t have to tell you, dear -Category Café reader, that string diagrams are extremely useful. They speed up computations massively, reveal what makes a proof tick without an impenetrable forest of details, and suggest properties that you might not even have thought about in algebraic notation. They also make your paper friendlier to read.
However, string diagrams are also a pain to typeset. First, there is the entrance fee of learning a modern LaTeX drawing package, like TikZ. Then, there is the learning period of setting up macros tailored to string diagrams and internalizing them in your muscle memory. But even after all that investment, it still takes a lot of time. And unlike that glorious moment when you realise that you have cycled about twice the circumference of the Earth in your life, this time is mostly wasted. I estimate I’ve wasted over 2000 string diagrams’ worth of time by now.
Wouldn’t it be great if you could simply draw your diagram by hand, and have it magically converted into TikZ? Now you can!
January 22, 2018
A Categorical Semantics for Causal Structure
Posted by John Baez
guest post by Joseph Moeller and Dmitry Vagner
We begin the Applied Category Theory Seminar by discussing the paper A categorical semantics for causal structure by Aleks Kissinger and Sander Uijlen.
Compact closed categories have been used in categorical quantum mechanics to give a structure for talking about quantum processes. However, they prove insufficient to handle higher order processes, in other words, processes of processes. This paper offers a construction for a -autonomous extension of a given compact closed category which allows one to reason about higher order processes in a non-trivial way.
We would like to thank Brendan Fong, Nina Otter, Joseph Hirsh and Tobias Heindel as well as the other participants for the discussions and feedback.
January 10, 2018
On the Magnitude Function of Domains in Euclidean Space, I
Posted by Simon Willerton
guest post by Heiko Gimperlein and Magnus Goffeng.
The magnitude of a metric space was born, nearly ten years ago, on this blog, although it went by the name of cardinality back then. There has been much development since (for instance, see Tom Leinster and Mark Meckes’ survey of what was known in 2016). Basic geometric questions about magnitude, however, remain open even for compact subsets of : Tom Leinster and Simon Willerton suggested that magnitude could be computed from intrinsic volumes, and the algebraic origin of magnitude created hopes for an inclusion-exclusion principle.
In this sequence of three posts we would like to discuss our recent article, which is about asymptotic geometric content in the magnitude function and also how it relates to scattering theory.
For “nice” compact domains in we prove an asymptotic variant of Leinster and Willerton’s conjecture, as well as an asymptotic inclusion-exclusion principle. Starting from ideas by Juan Antonio Barceló and Tony Carbery, our approach connects the magnitude function with ideas from spectral geometry, heat kernels and the Atiyah-Singer index theorem.
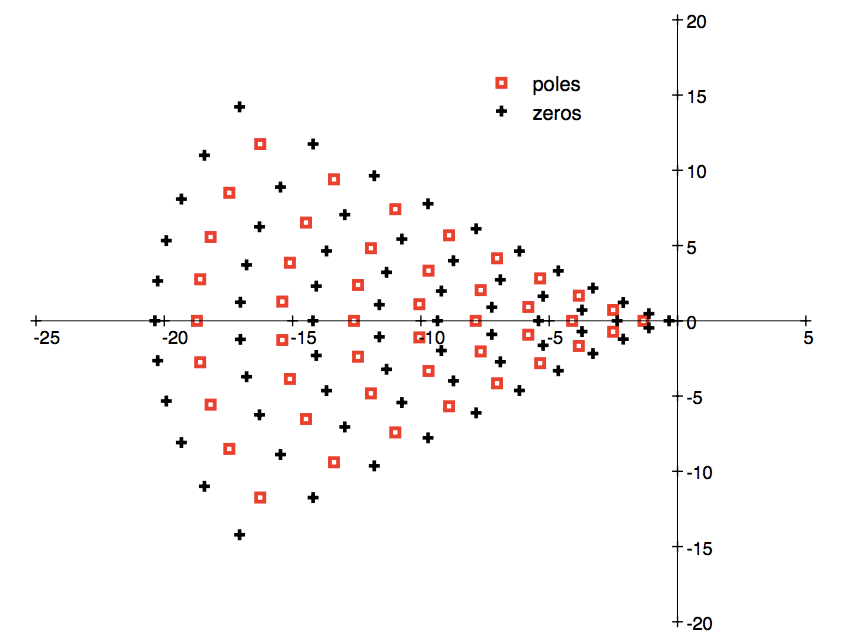
We will also address the location of the poles in the complex plane of the magnitude function. For example, here is a plot of the poles and zeros of the magnitude function of the -dimensional ball.
We thank Simon for inviting us to write this post and also for his paper on the magnitude of odd balls as the computations in it rescued us from some tedious combinatorics.
The plan for the three café posts is as follows:
State the recent results on the asymptotic behaviour as a metric space is scaled up and on the meromorphic extension of the magnitude function.
Discuss the proof in the toy case of a compact domain and indicate how it generalizes to arbitrary odd dimension.
Consider the relationship of the methods to geometric analysis and potential ramifications; also state some open problems that could be interesting.
 Posts with this logo use
Posts with this logo use