September 29, 2010
Jacob Biamonte on Tensor Networks
Posted by John Baez
One of the unexpected pleasures of starting work at the Centre for Quantum Technologies was realizing that the math I learned in loop quantum gravity and category theory can also be useful in quantum computation and condensed matter physics!
In loop quantum gravity I learned a lot about “spin networks”. When I sailed up to the abstract heights of category theory, I discovered that these were a special case of “string diagrams”. And now, going back down to earth, I see they have a special case called “tensor networks”.
Jacob Biamonte is a postdoc who splits his time between Oxford and the CQT, and he’s just finished a paper on tensor networks:
- Jacob Biamonte, Algebra and coalgebra on categorical tensor network states.
He’s eager to get your comments on this paper, since while it’s aimed at people who already know about tensor networks, it uses a lot of things we talk about here: for example, algebras and coalgebras in symmetric monoidal categories! So, if you folks can’t understand this paper, or find it insufficiently precise, he’d like to hear from you.
Heck, he’d also like to hear from you if you love the paper! But as usual, the most helpful feedback is not just a pat on the back, but a suggestion for how to make things better.
September 23, 2010
Fetishizing p-Values
Posted by Tom Leinster
The first time I understood the problem was when I read this:
values are not a substitute for real measures of effect size, and despite its popularity with researchers and journal editors, testing a null hypothesis is rarely the appropriate model in science [long list of references, from 1969 onwards]. In natural populations, the null hypothesis of zero differentiation is virtually always false, and if sample size is large enough, this can be demonstrated with any desired degree of statistical significance.
(Lou Jost, Molecular Ecology 18 (2009), 2088–2091.)
If Jost’s criticism is valid, it’s shockingly important. He is attacking what is perhaps the most common use of statistics in science.
September 22, 2010
Bacard on Segal Enriched Categories
Posted by Tom Leinster
Hugo Bacard, a PhD student at Nice working with Carlos Simpson, has just put a new paper on the arXiv: Segal enriched categories I. It’s all about homotopy-enrichment.
The basic aim is to study categories enriched — in an up-to-homotopy way — in a bicategory equipped with a class of 2-cells to be thought of as homotopy equivalences. It’s clear from the introduction that Bacard’s formalism covers a very wide range of structures indeed. For instance, you’ll see appearances made by homotopy algebras, torsors, discrete valuation rings, metric spaces, parallel transport functors, …. Even motivic cohomology gets a mention.
The exposition looks nice. There are also some unusual and intriguing pictures. Would anyone like to have a bash at writing a short summary?
September 15, 2010
Grothendieck-Maltsiniotis ∞-categories
Posted by Mike Shulman
Yesterday Georges Maltsiniotis posted a paper on the arXiv in which he presents a definition of -groupoid, said to be due to Grothendieck in Pursuing Stacks, and modifies it to give a similar definition of -categories. (These definitions have been available on his website for a while, but only in French.)
These “Grothendieck-Maltsiniotis” definitions are quite similar to that of Batanin, especially as modified by Leinster. The precise relationship between the two is studied in the thesis of D. Ara, a student of Maltsiniotis, but it’s not hard to get an intuitive idea of their similarities and differences.
September 14, 2010
What Is This Category Enriched In?
Posted by David Corfield
I’ve never felt completely happy with enriched category theory, so perhaps people could help me think through this example.
This question got me wondering again what can be said about a category of conditional probabilities. Let’s take as our objects finite sets, and morphisms to be of the form , a conditional probability distribution , that is, a row stochastic matrix. This is an arrow in the Kleisli category for the Giry monad. An equivalent category with column stochastic matrices is described by Tobias Fritz in A presentation of the category of stochastic matrices.
September 11, 2010
Categories and Information in Oxford
Posted by John Baez
What branch of mathematics is sufficiently general to apply both to quantum physics and linguistics? You guessed it:
- The categorical flow of information in quantum physics and linguistics, Oxford, October 29-31, 2010. Organized by Chris Heunen and Mehrnoosh Sadrzadeh.
September 7, 2010
Grothendieck’s “Tohoku” paper
Posted by John Baez
Michael Barr has spent a lot of time and effort translating Grothendieck’s legendary “Tohoku” paper into English. If you don’t mind violating Grothendieck’s stated wishes, you can now read this translation:
- Alexandre Grothendieck, On certain aspects of homological algebra, trans. Michael Barr.
It’s about abelian categories, sheaves of modules, resolutions, derived functors, and the Grothendieck spectral sequence.
September 6, 2010
Integral Geometry in Barcelona
Posted by Tom Leinster
Simon Willerton and I are currently at the Advanced Course on Integral Geometry and Valuation Theory at the Centre de Recerca Matemàtica, Barcelona. Over the next couple of days we’re going to be presenting our own work, along with some work of Mark Meckes, on magnitude of metric spaces. You can read my slides here, and when I see Simon next I’ll hassle him to make his slides available too—if he hasn’t already got the hint.
I’m a beginner in integral geometry, which makes this meeting an adventure. Over the last couple of years I’ve been trying to educate myself in the subject a bit. In particular, I was in Barcelona for the week before the course, at the kind invitation of Joachim Kock. He’s also attending the course, so we spent some time trying to get the basics straight. I think it’s paying off.
Since I’m such a novice, I’m not going to attempt a running summary of the talks. But just to give the flavour of the meeting, I’ll say a little about each of the first day’s talks.
September 1, 2010
Function T-Algebras on ∞-Stacks
Posted by Urs Schreiber
Over the course of this year, Herman Stel has been working on a master thesis and I have been advising him. Yesterday was the defense. See
- Herman Stel, -Stacks and their Function Algebras
Abstract For any abelian Lawvere theory, we establish a Quillen adjunction between model category structures on cosimplicial -algebras and on simplicial presheaves over duals of -algebras, whose left adjoint forms algebras of functions with values in the canonical -line object. We find mild general conditions under which this descends to the local model structure that models -stacks over duals of -algebras.
For the theory of associative algebras this reproduces the situation in Toën’s Champs affine . We consider the case where is the theory of smooth algebras: the case of synthetic differential geometry. In particular, we work towards a definition of smooth -vector bundles with flat connection. To that end we analyse the tangent category of the category of smooth algebras and Kock’s simplicial model for synthetic combinatorial differential forms which may be understood as an -categorification of Grothendieck’s de Rham space functor.
Bimonoids from Biproducts
Posted by John Baez
Today Jacob Biamonte and I were talking about Boolean circuits and we came across a cute fact I hadn’t noticed before. I’ll explain it, and then ask you to help me find a really slick proof.
But let’s start at the beginning. Suppose is a vector space. There’s a “diagonal map”
which goes like this:
There’s also an “codiagonal map”
which goes like this:
Yeah, it’s just addition.
Now say we draw the diagonal map as a green blob with one input and two outputs, and the codiagonal map as red blob with two outputs and one input. Then this law holds:
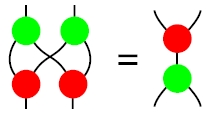
Why?
The Philosophy of the Logic of Sheaves
Posted by John Baez
An unusual conference in an unusual venue:
- Symposium on the Philosophy of the Logic of Sheaves, October 19 - 21, 2010, Universidad del Valle, Cali, Colombia.
Colin McLarty will be speaking about the work of Grothendieck!
 Posts with this logo use
Posts with this logo use 














