September 22, 2017
Lattice Paths and Continued Fractions II
Posted by Simon Willerton
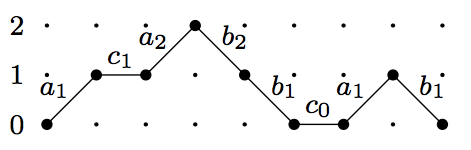
Last time we proved Flajolet’s Fundamental Lemma about enumerating Dyck paths. This time I want to give some examples, in particular to relate this to what I wrote previously about Dyck paths, Schröder paths and what they have to do with reverse Bessel polynomials.
We’ll see that the generating function of the sequence of reverse Bessel polynomials has the following continued fraction expansion.
I’ll even give you a snippet of SageMath code so you can have a play around with this if you like.
Applied Category Theory at UCR (Part 2)
Posted by John Baez
I’m running a special session on applied category theory, and now the program is available:
- Applied category theory, Fall Western Sectional Meeting of the AMS, 4-5 November 2017, U.C. Riverside.
This is going to be fun.
My former student Brendan Fong is now working with David Spivak at M.I.T., and they’re both coming. My collaborator John Foley at Metron is also coming: we’re working on the CASCADE project for designing networked systems.
Dmitry Vagner is coming from Duke: he wrote a paper with David and Eugene Lerman on operads and open dynamical system. Christina Vaisilakopolou, who has worked with David and Patrick Schultz on dynamical systems, has just joined our group at UCR, so she will also be here. And the three of them have worked with Ryan Wisnesky on algebraic databases. Ryan will not be here, but his colleague Peter Gates will: together with David they have a startup called Categorical Informatics, which uses category theory to build sophisticated databases.
That’s not everyone — for example, most of my students will be speaking at this special session, and other people too — but that gives you a rough sense of some people involved. The conference is on a weekend, but John Foley and David Spivak and Brendan Fong and Dmitry Vagner are staying on for longer, so we’ll have some long conversations… and Brendan will explain decorated corelations in my Tuesday afternoon network theory seminar.
Wanna see what the talks are about?
September 18, 2017
Lattice Paths and Continued Fractions I
Posted by Simon Willerton
In my last post I talked about certain types of lattice paths with weightings on them and formulas for the weighted count of the paths, in particular I was interested in expressing the reverse Bessel polynomials as a certain weighted count of Schröder paths. I alluded to some connection with continued fractions and it is this connection that I want to explain here and in my next post.
In this post I want to prove Flajolet’s Fundamental Lemma. Alan Sokal calls this Flajolet’s Master Theorem, but Viennot takes the stance that it deserves the high accolade of being described as a ‘Fundamental Lemma’, citing Aigner and Ziegler in Proofs from THE BOOK:
“The essence of mathematics is proving theorems – and so, that is what mathematicians do: They prove theorems. But to tell the truth, what they really want to prove, once in their lifetime, is a Lemma, like the one by Fatou in analysis, the Lemma of Gauss in number theory, or the Burnside-Frobenius Lemma in combinatorics.
“Now what makes a mathematical statement a true Lemma? First, it should be applicable to a wide variety of instances, even seemingly unrelated problems. Secondly, the statement should, once you have seen it, be completely obvious. The reaction of the reader might well be one of faint envy: Why haven’t I noticed this before? And thirdly, on an esthetic level, the Lemma – including its proof – should be beautiful!”
Interestingly, Aigner and Ziegler were building up to describing a result of Viennot’s – the Gessel-Lindström-Viennot Lemma – as a fundamental lemma! (I hope to talk about that lemma in a later post.)
Anyway, Flajolet’s Fundamental Lemma that I will describe and prove below is about expressing the weighted count of paths that look like
as a continued fraction
Next time I’ll give a few examples, including the connection with reverse Bessel polynomials.
September 12, 2017
Applied Category Theory 2018
Posted by John Baez
We’re having a conference on applied category theory!
- Applied Category Theory (ACT 2018). Summer school April 23rd to 27th and conference April 30th to May 4th 2018 at the Lorentz Center in Leiden, the Netherlands. Organized by Bob Coecke (Oxford), Brendan Fong (MIT), Aleks Kissinger (Nijmegen), Martha Lewis (Amsterdam), and Joshua Tan (Oxford).
The plenary speakers will be:
- Samson Abramsky (Oxford)
- John Baez (UC Riverside)
- Kathryn Hess (EPFL)
- Mehrnoosh Sadrzadeh (Queen Mary)
- David Spivak (MIT)
There will be a lot more to say as this progresses, but for now let me just quote from the conference website.
September 8, 2017
Postdoc in Applied Category Theory
Posted by John Baez
guest post by Spencer Breiner
One Year Postdoc Position at Carnegie Mellon/NIST
We are seeking an early-career researcher with a background in category theory, functional programming and/or electrical engineering for a one-year post-doctoral position supported by an Early-concept Grant (EAGER) from the NSF’s Systems Science program. The position will be managed through Carnegie Mellon University (PI: Eswaran Subrahmanian), but the position itself will be located at the US National Institute for Standards and Technology (NIST), located in Gaithersburg, Maryland outside of Washington, DC.
The project aims to develop a compositional semantics for electrical networks which is suitable for system prediction, analysis and control. This work will extend existing methods for linear circuits (featured on this blog!) to include (i) probabilistic estimates of future consumption and (ii) top-down incentives for load management. We will model a multi-layered system of such “distributed energy resources” including loads and generators (e.g., solar array vs. power plant), different types of resource aggregation (e.g., apartment to apartment building), and across several time scales. We hope to demonstrate that such a system can balance local load and generation in order to minimize expected instability at higher levels of the electrical grid.
This post is available full-time (40 hours/5 days per week) for 12 months, and can begin as early as October 1st.
For more information on this position, please contact Dr. Eswaran Subrahmanian (sub@cmu.edu) or Dr. Spencer Breiner (spencer.breiner@nist.gov).
 Posts with this logo use
Posts with this logo use