Lattice Paths and Continued Fractions II
Posted by Simon Willerton
Last time we proved Flajolet’s Fundamental Lemma about enumerating Dyck paths. This time I want to give some examples, in particular to relate this to what I wrote previously about Dyck paths, Schröder paths and what they have to do with reverse Bessel polynomials.
We’ll see that the generating function of the sequence of reverse Bessel polynomials has the following continued fraction expansion.
I’ll even give you a snippet of SageMath code so you can have a play around with this if you like.
Flajolet’s Fundamental Lemma
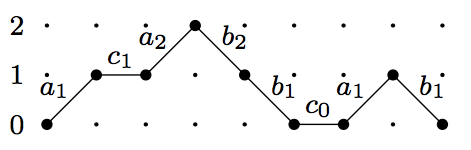
Let’s just recall from last time that if we take Motzkhin paths weighted by s, s and s as in this example,
then when we sum the weightings of all Motzkhin paths together we have the following continued fraction expression.
Jacobi continued fractions and Motzkhin paths
Flajolet’s Fundamental Lemma is very beautiful, but we want a power series going up in terms of path length. So let’s use another variable to keep track of path length. All three types of step in a Motzkhin path have length one. We can set , and . Then , and the coefficient of will be the sum of the weights of Motzkhin paths of length . This coefficient will be a polynomial (rather than a power series) as there are only finitely paths of a given length.
Such a continued fraction is called a Jacobi (or J-type) continued fraction. They crop up in the study of moments of orthogonal polynomials and also in birth-death processes.
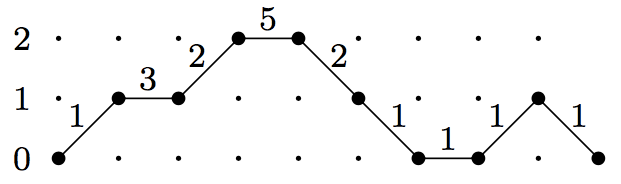
For example, I believe that Euler proved the following Jacobi continued fraction expansion of the generating function of the factorials. We can get the right hand side by taking and . Here is a Motzkhin path weighted in that way.
The equation above is telling us that if we weight Motzkhin paths in that way, then the weighted count of Motzkhin paths of length is , and that deserves an exclamation mark! (You’re invited to verify this for Motzkhin paths of length 4.)
I’ve put some SageMath code at the bottom of this post if you want to check the continued fraction equality numerically.
Stieltjes continued fractions and Dyck paths
A Dyck path is a Motzkhin path with no flat steps. So if we weight the flat steps in Motzkhin paths with then when we do a weighted count then we just count the weighted Dyck paths. This means setting .
Also the weigh on an up step always appears with the weight on a corresponding down step (what goes up must come down!) so we can simplify things by just putting a weighting — which we’ll rename as — on the down step from level and put a weighting of on each up step. We can call this weighting .
Putting this together we get the following, where we’ve noted that there are no Dyck paths of odd length.
This kind of continued fraction is called a Stieltjes (or S-type) continued fraction. Of course, we could replace by in the above, without any ill effect.
Previously we proved combinatorially that with the weighting where the weighted count of Dyck paths of length was precisely . This means that we have proved the following continued fraction expansion of the generating function of the odd double factorials.
I believe this was originally proved by Gauss, but I have no idea how.
Again there’s some SageMath code at the end for you to see this in action.
Thron continued fractions and Schröder paths
What I’m really interested in, you’ll remember, is reverse Bessel polynomials, and these are giving weighted counts of Schroder paths. Using continued fractions in this context is less standard than for Dyck paths and Motzkhin paths as above, but it only requires a minor modification. I learnt about this from Alan Sokal.
The difference between Motzkhin paths and Schröoder paths is that the flat steps have length in Schroder paths. Remember that the power of was encoding the length, so we just have to assign to each flat step rather than . So if we put , and in Flajolet’s Fundamental Lemma then we get the following.
Here is the weighting where we put s on the down steps and s on the flat steps.
This kind of continued fraction is called a Thron (or T-type) continued fraction. Again, we could replace by in the above, without any ill effect.
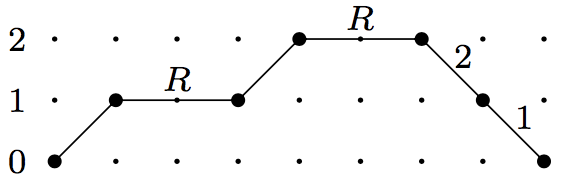
We saw before that if we take the weighting, , with and , such as in the following picture,
then the weighted sum of Schroder paths of length is precisely the th reverse Bessel polynomial:
Putting that together with the Thron continued fraction above we get the following Thron continued fraction expansion for the generating function of the reverse Bessel polynomials.
This expression is given by Paul Barry, without any reference, in the formulas section of the entry in the Online Encyclopedia of Integer Sequences.
See the end of the post for some SageMath code to check this numerically.
In my recent magnitude paper I actually work backwards. I start with the continued fraction expansion as a given, and use Flajolet’s Fundamental Lemma to give the Schr&\ouml;der path interpretation of the reverse Bessel polynomials. Of course, I now know that I can bypass the use of continued fractions completely, and have a purely combinatorial proof of this interpretation. Regardless of that, however, the theory of lattice paths and continued fractions remains beautiful.
Appendix: Some SageMath code
It’s quite easy to play around with these continued fractions in SageMath, at least to some finite order. I thought I’d let you have some code to get you started…
Here’s some SageMath code for you to check the Jacodi continued fraction expansion of the generating function of the factorials.
# T = Z[t]
T.<t> = PolynomialRing(ZZ)
# We'll take the truncated continued fraction to be in the
# ring of rational functions, P = Z(t)
P = Frac(T)
def j_ctd_frac(alphas, gammas):
if alphas == [] or gammas == []:
return 1
else:
return P(1/(1 - gammas[0]*t - alphas[0]*t^2*
j_ctd_frac(alphas[1:], gammas[1:])))
cf(t) = j_ctd_frac([1, 4, 9, 16, 25, 36], [1, 3, 5, 7, 9, 11])
print cf(t).series(t, 10)
The above code can be used to define a Stieltjes continued fraction and check out the expansion of Gauss on the odd double factorials.
def s_ctd_frac(alphas):
gammas = [0]*len(alphas)
return j_ctd_frac(alphas, gammas)
cf(t) = s_ctd_frac([1, 2, 3, 4, 5, 6])
print cf(t).series(t, 13)
Here’s the code for getting the reverse Bessel polynomials from a Thron continued fraction.
S.<R> = PolynomialRing(ZZ)
T.<t> = PowerSeriesRing(S)
def t_ctd_frac(alphas, gammas):
if alphas == [] or gammas == []:
return 1
else:
return (1/(1- gammas[0]*t^2 - alphas[0]*t^2*
t_ctd_frac(alphas[1:], gammas[1:])))
print T(t_ctd_frac([1, 2, 3, 4, 5, 6], [R, R, R, R, R, R]),
prec=13)

Re: Lattice Paths and Continued Fractions II
Cool! All this has a lot of overlap with this old blog post of mine, although I didn’t know the names of most of the objects and results I was writing down.