Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

January 22, 2014

The Magnitude of a Graph

Posted by Tom Leinster

I’ve just arXived a new paper about a new invariant, The magnitude of a graph. Much of the development of this invariant has taken place at this blog, with two previous posts and crucial contributions from David Speyer and Simon Willerton. Your comments, critical or otherwise, would be very welcome.

Magnitude seems to be orthogonal to other graph invariants. You can’t derive from it such classic invariants as the Tutte polynomial or the chromatic number, nor the girth nor the clique number nor even the number of connected components. And conversely, you can’t derive the magnitude from these or any other well-known graph invariants. Apparently, it captures information of a different kind.

Its most appealing characteristic is that it behaves like cardinality. It’s multiplicative with respect to cartesian product, additive with respect to disjoint union, and obeys a restricted version of the inclusion-exclusion principle. And it also behaves a bit like the Tutte polynomial. For instance, it’s often invariant under Whitney twists — though not always, as I’ll explain.

That it behaves like cardinality is no surprise, given its origins.

Steve Schanuel taught us that the Euler characteristic of a space should be thought of as analogous to the cardinality of a set. There is a notion of the Euler characteristic of a category, closely related to other forms of Euler characteristic. This notion can be generalized to enriched categories, then specialized to categories enriched in the poset (ℕ,≥)(\mathbb{N}, \geq), seen as a monoidal category via addition. Any graph gives rise to an ℕ\mathbb{N}-enriched category, the objects being the vertices and the homs being distances in the graph. So, we get an invariant of graphs — and that’s what’s called magnitude.

That’s a highly condensed account, and you can find out more by following the links, but let me skip all that and tell you the end result, which is completely concrete.

The magnitude #G\# G of a graph GG is a rational function over ℚ\mathbb{Q} — the ratio of two polynomials with integer coefficients. It can also be expressed as a power series over ℤ\mathbb{Z}. For example, the graph

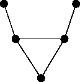
bull graph

has magnitude

5+5q−4q 2(1+q)(1+2q)=5−10q+16q 2−28q 3+52q 4−100q 5+…. \frac{5 + 5q - 4q^2}{(1 + q)(1 + 2q)} = 5 - 10q + 16q^2 - 28q^3 + 52q^4 - 100q^5 + \ldots.

Here qq is just a formal variable.

The definition goes like this. Take a graph GG. Let ZZ be the square matrix whose rows and columns are indexed by the vertices of GG, and whose entries are given by

Z(x,y)=q d(x,y) Z(x, y) = q^{d(x, y)}

for each pair of vertices xx and yy. Here d(x,y)d(x, y) is the distance between xx and yy in the graph (and by convention, q ∞=0q^\infty = 0). It turns out that ZZ is invertible over both the field ℚ(q)\mathbb{Q}(q) of rational functions and the ring ℤ[q]\mathbb{Z}[q] of power series. The magnitude of GG is the sum of all the entries of its inverse.

I know of no direct graph-theoretic motivation for this definition. Frankly, it looks odd. The real motivation is that it’s part of a large family of related invariants, including not only cardinality and various types of Euler characteristic, but also metric dimension, maximum entropy, and, conjecturally, geometric measures like volume, surface area and perimeter. From that point of view, it would be odd if graph magnitude wasn’t important.

The paper has two main theorems. First, magnitude obeys an inclusion-exclusion principle: when GG and HH are subgraphs of some larger graph, and certain further conditions hold,

#(G∪H)=#G+#H−#(G∩H) \# (G \cup H) = \#G + \#H - \#(G \cap H)

(Theorem 4.9). I was frustrated by having to impose those “further conditions”, because it meant that magnitude didn’t behave entirely like cardinality. But then I figured out that no nontrivial graph invariant behaves entirely like cardinality (Lemma 4.1).

The second main theorem was conjectured by Simon. Take a graph with two distinct vertices distinguished, and another graph with two distinct vertices distinguished. Glue them together by pairing up the distinguished vertices. There are two different ways you can do this, depending on how you do the pairing, and the two resulting graphs are said to differ by a Whitney twist.

David Speyer pointed out that (as all graph theorists know) the Tutte polynomial is invariant under Whitney twists, so if magnitude is a specialization of the Tutte polynomial, it had better be invariant too. Then David got his computer to randomly generate a couple of 18-vertex graphs differing by a Whitney twist, and lo and behold, their magnitudes were equal. That magnitude was a rational function of degree 23 whose coefficients were integers of up to 5 decimal digits, so it was highly unlikely that this happened by chance.

So, when Simon found an example showing that magnitude isn’t invariant under Whitney twists, it came as a considerable surprise. What’s going on?

Well, Simon immediately conjectured that you get invariance only when the two points of identification are joined by an edge in one of the original two graphs. That turns out to be true — and that’s the second theorem.

The apparently implausible coincidence in David’s experiment can therefore be explained as follows. He generated two 10-vertex graphs GG and HH, putting an edge between each pair of vertices with probability 0.40.4. He then joined them together in two ways, giving two 18-vertex graphs XX and YY differing by a Whitney twist. The second theorem applies if XX (or equivalently YY) has an edge between the two points of identification, and the probability that this happens is 1−(1−0.4) 2=0.641 - (1 - 0.4)^2 = 0.64. So, it was more likely than not that he’d get what he got.

Posted at January 22, 2014 12:19 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2686



15 Comments & 0 Trackbacks

Re: The Magnitude of a Graph

Incidentally, the grammar of the title of the paper is dedicated, with affection, to John Baez. When I finished my paper The magnitude of metric spaces, John wrote to me specifically to complain that I should have called it “The magnitude of a metric space”, teasing me with outrageously unfair comparisons between my actual title and “The Sound of Musics”, “The Joy of Sexes”, and so on. I replied not only in kind (making up an undergraduate textbook called “The Solution of an Ordinary Differential Equation”), but also by Latexing a retitled version of the paper especially for him. So: John, this title’s for you.

Posted by: Tom Leinster on January 22, 2014 12:51 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

I have to say, I don’t think either one of you has a strong case. John’s comparisons certainly are outrageously unfair, since “space” in your title is a count noun, but “Music” and “Sex” are, in those classic titles, mass nouns — no one would have thought of the titles “The Sound of a Music” or “The Joy of a Sex”.

On the other hand, it’s perfectly normal, especially in a title, to interpret a noun phrase with a singular indefinite article in an abstract or generic sense. Particularly if you read “Solution” as meaning “the process of solving”, then “The Solution of an Ordinary Differential Equation” strikes me as a potentially reasonable title, depending on the content of the book. (My major objections would be that an undergraduate textbook on ODEs should discuss 1) systems of ODEs, which appear to be excluded by the singular in the title; and 2) modeling with ODEs and qualitative analysis of solutions, which appear to be excluded by the word “solution”.)

Bottom line: I think “The magnitude of a metric space” and “The magnitude of graphs” are equally reasonable titles.

Of course, the definition of magnitude for metric spaces involves an arbitrary choice of scale (which you’ve cleverly avoided in the case of graphs by defining the magnitude to be a function instead of a number). So if you’d arranged the definitions a little differently, it could also have made sense to write about “The magnitudes of a metric space” or “The magnitudes of metric spaces”.

Posted by: Mark Meckes on January 22, 2014 8:11 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

Thanks, Tom! Sounds like an interesting paper. I’m honored.

Posted by: John Baez on January 22, 2014 9:53 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

Indeed, wasn’t there a paper titled something like “Invariants of four manifolds”? It actually involved many more than that.

Posted by: Allen Knutson on January 22, 2014 6:35 PM | Permalink | Reply to this

Re: The Magnitude of a Graph

Here’s a somewhat irrelevant question that someone interested in Tom’s post might know the answer to.

By ‘graph’ I’ll actually mean a directed multigraph, i.e. a pair of finite sets and functions

s,t:E→V s, t : E \to V

But people may have thought about this question for other kinds of graphs.

I’ll consider graphs whose edges are labelled by numbers in (0,∞)(0,\infty). I’ll call these numbers the lengths of the edges.

Consider the set of isomorphism classes of graphs whose edges have lengths. There seems to be an obvious best way to make this into a topological space XX such that:

1) if we choose a graph and continuously change the lengths of its edges, the corresponding point in XX traces out a continuous path, and

2) if we choose a graph and let the length of an edge approach zero, the corresponding point in XX approaches the point corresponding to a new graph where that edge has been collapsed.

I’m being a bit vague here but I hope you get the idea, because it’s supposed to be a very simple idea.

My question is just: is this some known thing? It’s a kind of ‘moduli space of graphs whose edges have lengths’.

I need this thing for my work with Brendan Fong on electric circuits, and I’m not eager to reinvent the wheel.

But also, just to make a connection with what Tom is talking about, one might hope to be able to define a concept of magnitude for graphs whose edges have lengths (maybe using simple graphs instead of directed multigraphs). In fact I bet he’s already done it. And I’d hope this magnitude is a continuous function on the moduli space I’m thinking about (or the version for simple graphs).

Posted by: John Baez on January 22, 2014 10:29 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

It’s not quite the same, but this seems related to the Gromov–Hausdorff topology on the set of isometry classes of compact metric spaces. In fact every finite metric space can be viewed as a weighted simple graph, although not in a unique way, so the Gromov–Hausdorff topology on finite metric spaces is probably a quotient space of your XX.

If you forget everything about a weighted simple graph except its shortest-path metric, then it has a notion of magnitude as a metric space. When the weights are all equal to tt, then you get the notion of magnitude Tom’s describing here by substituting q=e −tq = e^{-t}, and as Tom discussed above the magnitude is a rational function of qq, which may have singularities. You can also have a jump discontinuity at t=0t = 0.

Posted by: Mark Meckes on January 22, 2014 11:52 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

To add to Mark’s answer: if you fix the vertex-set and allow the distances/edge-lengths to vary continuously, then the magnitude varies continuously. It’s only when vertices merge or split that discontinuities may arise. For instance, Simon discovered a particular 6-vertex graph which, when scaled down gradually, has magnitude converging to 6/56/5; yet the limit of this scaling process is the 1-vertex graph, which has magnitude 11.

Your moduli space reminded me strongly of this kind of thing, but I expect you already thought about that :-)

Posted by: Tom Leinster on January 22, 2014 12:18 PM | Permalink | Reply to this

Re: The Magnitude of a Graph

Thanks, Mark and Tom! It sounds like neither of you are claiming to have seen anyone talk about a ‘moduli space of graphs with lengths for edges’… even though this would be one natural context in which to formalize a remark like

To add to Mark’s answer: if you fix the vertex-set and allow the distances/edge-lengths to vary continuously, then the magnitude varies continuously.

But I guess you can also formalize this in terms of the set of isometry classes of finite metric spaces, equipped with its Gromov–Hausdorff metric… so you might never have have felt the need for a ‘moduli space of graphs with lengths for edges’.

Two reasons I want it are:

1) electrical circuits made of resistors, where ‘edges’ are wires, ‘length’ is resistance and I want to collapse any edge of zero resistance,

2) Markov processes, where ‘vertices’ are states, ‘edges’ are allowed transitions from one state to another, ‘length’ is the reciprocal of the transition rate, and again I want to collapse edges of zero length.

The first application works fine with undirected graphs, while the the second really needs directed graphs, and both are happy with directed multigraphs.

Your moduli space reminded me strongly of this kind of thing, but I expect you already thought about that :-)

Actually I hadn’t! — even though I’m writing a paper on this sort of thing right now with a grad student named Nina Otter, who has been visiting UCR from ETH Zürich and wants to work on applications of ‘higher mathematics’ to biology.

It goes to show that I have a limited set of thoughts bouncing around my little brain, but still not enough wit to notice how similar some of these thoughts are.

I think the reason I didn’t make the connection is that in ‘this sort of thing’ the numbers labelling edges have the meaning of ‘time’, while in 1) and 2) they have the meaning of ‘resistance’ or ‘inverse rate’: how hard it is to get from one place to another.

And for some reason, ‘time’ and ‘inverse rate’ were filed in slightly different locations in that little brain.

(By the way, ‘higher mathematics’ is Alan Weinstein’s term for math related to higher categories.)

Posted by: John Baez on January 23, 2014 10:40 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

I have seen century old textbooks called On Higher Algebra or some variation on that theme, and they were about matrices. A fair cry from the Higher Algebra of our time…

Posted by: David Roberts on January 23, 2014 10:49 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

Thinking about connecting up the notions of phylogenetic tree and resistor network made me wonder whether biologists ever talked about “evolutionary resistance” — the difficulty of evolving from one state to another. Lo and behold, a 5-second web search brought up this:

Size as a line of least evolutionary resistance: diet and adaptive morphological radiation in New World monkeys.

I also remember Lou Jost talking about the concept of “evolutionary work” at the diversity research programme in Barcelona.

Posted by: Tom Leinster on January 23, 2014 11:54 AM | Permalink | Reply to this

Re: The Magnitude of a Graph

Hi John,

You probably know this. There is one nice category of directed graphs where you can map edges to “vertices”: it’s the category of reflexif graphs (it may have other names as well). It’s a presheaf on a category with two objects and 3 non-identity morphisms – call them source, target and unit. Or, if you prefer, one insists that there is a distinguished identiy arrow attached to every vertex of the graph.

The products in this category look somewhat nicer than in the category of directed multigraphs.

Posted by: Eugene on January 23, 2014 5:54 PM | Permalink | Reply to this

Re: The Magnitude of a Graph

What you’re describing sounds a lot like outer space

Posted by: David Speyer on January 23, 2014 11:15 PM | Permalink | Reply to this

Re: The Magnitude of a Graph

I see that others above have already reminded you of the space of phylogenetic trees. It is now well understand that this is the tropical moduli space of n points on a genus 0 curve.

Everyone in the tropical world has known for a while that outer space should be more or less the tropical moduli space of genus g curves, and there should be some blend of outer space and tree space to get n points on a genus g curve. I’m not sure who to credit with getting the details right first, but Caporaso’s exposition looks good to me.

Posted by: David Speyer on January 23, 2014 11:25 PM | Permalink | Reply to this

Re: The Magnitude of a Graph

David wrote:

I see that others above have already reminded you of the space of phylogenetic trees.

Yes. Actually it’s more embarrassing: Tom was reminding me of my own work on the space of phylogenetic trees, and their relation with operads and Markov processes. This was inspired by the work of Susan Holmes et al that you linked to—I saw her talk about it in Singapore. But I hadn’t known about the connection to tropical geometry! Great, thanks! Yet another mysterious piece in the huge puzzle!

Everyone in the tropical world has known for a while…

But not in Singapore.

Posted by: John Baez on January 25, 2014 6:21 PM | Permalink | Reply to this

Knot invariants

Here’s a naive question. There are well-established connections between graph invariants and knot invariants, e.g. between the Tutte and Jones polynomials (very brief description). Can we, therefore, get a knot invariant out of magnitude?

Posted by: Tom Leinster on January 23, 2014 11:59 AM | Permalink | Reply to this

Post a New Comment