The Shannon Capacity of a Graph, 1
Posted by Tom Leinster
You’ve probably had the experience where you spell your name or address down the phone, and the person on the other end mistakes one letter for another that sounds similar: P sounds like B, which is easily mistaken for V, and so on. Under those circumstances, how can one most efficiently communicate without risk of error?
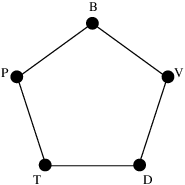
Shannon found the answer, but this isn’t part of his most famous work on communication down a noisy channel. There, the alphabet has no structure: any substitution of letters is as likely as any other. Here, the alphabet has the structure of a graph.
Today, I’ll explain Shannon’s answer. Next time, I’ll explain how it’s connected to the concept of maximum diversity, and thereby to magnitude.
First, let’s work through the example shown. We have some message that we want to communicate down the phone, and for some reason, we have to encode it using just the letters P, B, V, D and T. But P could be confused with B, B with V, V with D, D with T, and T with P. (I admit, T probably wouldn’t be confused with P, but I wanted to get a 5-cycle. So let’s go with it.) Our aim is to eliminate all possibility of confusion.
One way to do this would be to only communicate using P and V — or any other pair of non-adjacent vertices on the graph. This would certainly work, but it seems a shame: we have five letters at our disposal, and we’re not managing to do any better than if we had just two. In other words, we’re only communicating one bit of information per letter transmitted. That’s not very efficient.
There’s something smarter we can do. Let’s think not about single letters, but pairs of letters. How many non-confusable ordered pairs are there? Certainly, none of the pairs
(P, P), (P, V), (V, P), (V, V)
could be mistaken for any of the others. That’s still no improvement on a two-letter alphabet, though. But more sneakily, we could use
(P, P), (B, V), (V, T), (D, B), (T, D).
These are mutually distinguishable. To explain why, it will probably make life easier if I switch from letters to numbers, so that the graph becomes
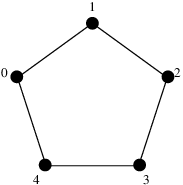
and the five pairs listed are
(0, 0), (1, 2), (2, 4), (3, 1), (4, 3).
For instance, if I transmit (1, 2) then you might hear (1, 1), or (0, 3), or in fact any of nine possibilities; but since the only one of them that’s on the list is (1, 2), you’d know you’d misheard. (In other words, you’d detect the error. You wouldn’t be able to correct it: for instance, (0, 3) could equally be a mishearing of (4, 3).)
What this means is that using two letters, we can transmit one of five possibilities. And that’s an improvement on binary. It’s as if we were using an alphabet with reliably distinguishable letters.
Obviously, we could take this further and use blocks of letters rather than , hoping for further savings in efficiency. In this particular example, it turns out that there’s nothing more to be gained: the five-pair coding is the best there is. In the jargon, the ‘Shannon capacity’ of our graph is .
All I’ll do in the rest of the post is state the general definition of Shannon capacity. I’ll need to take a bit of a run-up.
For the purposes of this post, a graph is a finite, undirected, reflexive graph without multiple edges. ‘Reflexive’ means that every vertex has a loop on it (that is, an edge from it to itself). Typically, graph theorists deal with irreflexive graphs, in which no vertex has a loop on it.
In a slightly comical way, reflexive and irreflexive graphs are in canonical one-to-one correspondence. (Simply adjoin or delete loops everywhere.) But there are two reasons why I want to buck the convention and use reflexive graphs:
As in the example, the vertices of the graph are supposed to be thought of as letters, and an edge between two letters means that one could be heard as the other. On that basis, every vertex should have a loop on it: if I say P, you might very well hear P!
The homomorphisms are different. A graph homomorphism is a map of the underlying vertex-set that preserves the edge-relation: if is adjacent to then is adjacent to . If and are two irreflexive graphs, and and the corresponding reflexive graphs, then , and in general it’s a proper subset. In other words, there is a proper inclusion of subcategories
which is bijective on objects. As we’ll see, products in the two categories are different, and that will matter.
Coming back to communication down a noisy phone line, a set of letters is ‘independent’ if none of them can be mistaken for any of the others. Formally, given a graph , an independent set in is a subset of the vertices of such that if are adjacent then .
The independence number of a graph is the largest cardinality of an independent set in . For example, when is the 5-cycle above, is an independent set and . It’s the “effective size of the alphabet” if you’re taking things one letter at a time.
To upgrade to the superior, multi-letter approach, we need to think about tuples of vertices — in other words, products of graphs.
In graph theory, there are various products of interest, and there’s a sort of hilarious convention for the symbol used. It goes as follows. Let denote the graph o—o consisting of two vertices joined by an edge, and suppose we have some kind of product of graphs. Then the convention is that the symbol used to denote that product will be a picture of the product of with itself. For example, this is the case for the products , , and .
The last one, , is called the strong product, and it’s what we want here. It’s simply the product in the category of reflexive graphs. Explicitly, the vertex-set of is the product of the vertex-sets of and , and is adjacent to iff is adjacent to and is adjacent to . You can check that is the graph that looks like .
(If we’d worked in the category of irreflexive graphs, we’d have got a different product: it’s the one denoted by .)
Let’s check that the strong product is really what we want for our application. Two vertices are supposed to be adjacent if one could be confused with the other. Put another way, two vertices are non-adjacent if they can be reliably distinguished from each other. We can distinguish from if either we can distinguish from or we can distinguish from . So, and should be non-adjacent if either and are non-adjacent or and are non-adjacent. And that’s just what happens in the strong product.
For instance, let be the 5-cycle shown above. Then the vertices
(0, 0), (1, 2), (2, 4), (3, 1), (4, 3).
of form an independent set of cardinality 5. It’s not hard to see that there’s no larger independent set in , so
—that is, has independence number .
For trivial reasons, if is an independent set in and is an independent set in then is an independent set in . We saw this in the case and . Hence
In particular,
or equivalently,
In our example, this says that . In fact, we know that , which represents an improvement: more economical communication.
The Shannon capacity measures how economically one can communicate without ambiguity, allowing the use of letter blocks of arbitrary size. Formally, the Shannon capacity of a graph is
For instance, we saw that . This means that if you want to communicate using vertices of , avoiding ambiguity, then you can do it as fast as if you were communicating with an alphabet containing completely distinguishable letters. You might call it the “effective number of vertices” in the graph… a phrase I’ll come back to next time.
Shannon also showed that
I don’t know the proof. Also, I don’t know whether is actually increasing in , which would of course imply this. (Update: Tobias Fritz answers both questions in a comment below.)
Update A few minutes after posting this, I discovered a coincidence: the Shannon capacity of a graph was also the subject of a blog post by Kenneth Regan at Buffalo, just a month ago. He also discusses the Lovász number of a graph, a quantity related to the Shannon capacity which I’d planned to mention next time.
The Shannon capacity is very hard to compute. Regan mentions that even the Shannon capacity of the 7-cycle is unknown!
Next time: How this connects to the concepts of maximum diversity and magnitude.


Re: The Shannon Capacity of a Graph, 1
Here is some more information; I’ve recently been looking at the Shannon capacity of graphs in the context of quantum contextuality, so I can say a little bit more.
The sequence is not monotonically increasing or non-decreasing in general. I think that itself is an example of this, where . Other surprising behaviors of such “independence sequences” have been found in a paper of Alon and Lubetzky.
That the independence sequence nevertheless converges is due to , which holds since the cartesian product of an independent set in with an independent set in is an independent set in . This inequality implies convergence of the sequence by virtue of Fekete’s lemma for superadditive sequences.
Looking forward to see how Shannon capacity relates to diversity and magnitude!