Tutte Polynomials and Magnitude Functions
Posted by Tom Leinster
Last summer in Barcelona, Joachim Kock floated the idea that there might be a connection between two invariants of graphs: the Tutte polynomial and the magnitude function. Here I’ll explain what these two invariants are, I’ll give you some examples, and I’ll ask for your help in understanding what the magnitude function tells us.
The Tutte polynomial of a graph is old and well-understood. It turns a graph into a polynomial in two variables, with natural number coefficients: The magnitude function of a graph is new and ill-understood. It turns a graph into a rational function in one variable, with rational coefficients: It can also be expanded as a power series with integer coefficients: I can’t figure out what the relationship between the two is — if any — or what information is contained in the magnitude function. It’s exasperating! I’ll be very pleased if someone can shed light on the situation.
In this post, “graphs” are always going to be finite and undirected. But some of the time I’ll allow loops and multiple edges, and some of the time I won’t. I’ll say which I’m doing.
(Formally, a graph with loops and multiple edges consists of a finite set , a finite set , and a map . Here is the quotient of by the obvious action of the group of order ; it can be seen as the set of subsets of of cardinality 1 or 2. A graph without loops or multiple edges consists of a finite set and a subset that, seen as a relation on , is symmetric and irreflexive.)
The Tutte polynomial
The Tutte polynomial knows a lot about a graph. It knows how many edges the graph has, how many maximal forests it contains, and how many ways there are to colour each of its vertices from a palette of 38 colours without ever giving the same colour to adjacent vertices. It’s related to the Potts model in statistical physics and the Jones polynomial of knot theory.
I’ll give you the definition in a moment, but first we need some terminology.
For this part, graphs will be allowed to have loops and multiple edges. Given an edge of a graph , there are two fundamental operations we can perform:
Deletion. The graph is simply with the edge removed (but the vertices left untouched).
Contraction. The graph is formed from by first removing , then identifying the two vertices that it used to join.
An edge is called a bridge if has more connected-components than , and a loop if it joins a vertex to itself.
The Tutte polynomial of a graph is characterized by the following two conditions:
if is neither a bridge nor a loop;
if consists of bridges, loops, and no other edges.
It takes some work to prove that there’s any polynomial with these two properties, since in the first condition there are usually many different edges we could choose. But this form of the definition has the advantage that it provides a nice algorithm for calculating Tutte polynomials. For instance, here’s a picture from Wikipedia of the algorithm at work:
The conclusion is that if is the five-vertex graph at the top of the tree then
The magnitude function
I’ll say twice what the magnitude function of a graph is: once for people who know what the magnitude of a metric space is, and once for people who don’t. In this part, graphs are not allowed to have loops or multiple edges — or more exactly, they could do, but adjoining or deleting loops or duplicate edges doesn’t make any difference to the magnitude function.
First, here’s the explanation for if you know about magnitude of metric spaces. Every finite metric space has a magnitude function , where is scaled up by a factor of and the bars indicate magnitude. (This “function” may have a finite number of singularities.) We can turn a graph into a metric space by taking the points to be the vertices and the distance between two vertices to be the number of edges in a shortest path joining them. The magnitude function of a graph is the magnitude function of the resulting metric space. It will be convenient to make the substitution and write .
Now here’s a direct explanation.
List the vertices in some order: . (The choice of order won’t affect anything.) Let be the number of edges in a shortest path from to (assuming there is one). Let be the square matrix over whose -entry is , or if there is no path from to .
We’re going to want to invert , so let’s consider its determinant. It’s a polynomial in . Also, , so ; hence is not the zero polynomial. It follows that the matrix is invertible over , the field of rational functions with rational coefficients. We define
to be the sum of all entries of the inverse matrix . This is the magnitude function of the graph .
It’s a fact that the magnitude function of a graph can always be expanded as a power series with integer coefficients. This is a special property of : your average rational function over is merely a Laurent series with rational coefficients.
(The key to the proof is that the constant term of the polynomial is , which is invertible in . It follows that can be expanded as a power series over . Hence can be too.)
What does the magnitude function tell us about a graph?
I’ll come clean: I have no direct evidence that the magnitude function of a graph tells us anything interesting about it. However, in several other settings, magnitude and related invariants have proven to be very fruitful, producing important quantities associated to topological spaces, metric spaces, sets, groupoids, orbifolds, associative algebras, etc. So it’s a good bet that it’s going to be fruitful for graphs too.
Moreover, in the particularly interesting setting of metric spaces, magnitude has been particularly reluctant to give up its secrets. So, the lack of obvious interpretation for the magnitude function of a graph doesn’t make me think it’s less likely to be interesting: it makes me wonder what it’s hiding!
But what does the magnitude function tell us? It’s hard to see. For instance, take the 4-cycle :
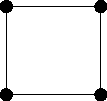
We have
How can we interpret this? It’s tempting to try to understand a power series over as the generating function of something, but what? Even ignoring the negative signs, what’s being counted here?
For another example, take to be a forest with vertex-set and edge-set . Then
where is the set of connected-components of . What is this function telling us about the graph?
Tutte vs. magnitude
In some ways, the information contained in the magnitude function seems to be complementary to that contained in the Tutte polynomial. For example:
the magnitude function knows how many vertices a graph has, but the Tutte polynomial doesn’t (at least if we’re allowing disconnected graphs)
the Tutte polynomial knows how many edges a graph has, but the magnitude function doesn’t (at least if we’re allowing multiple edges).
In other ways, the magnitude function and the Tutte polynomial seem more similar than complementary. Let’s consider some families of graphs known to have the same Tutte polynomial:
all trees with a given number of edges have the same Tutte polynomial; they also have the same magnitude function.
The three graphs known as the bull, the (3,2)-tadpole and the cricket (shown below) all have the same Tutte polynomial; they also all have the same magnitude function.
In fact, it’s consistent with the evidence below that for connected graphs, the Tutte polynomial determines the magnitude function.
However, in examples such as those above, I see no way of transforming the Tutte polynomial into the magnitude function. One way of proving that such a transformation exists would be to use the so-called “universal property” of the Tutte polynomial. (I don’t know whether it’s a universal property in the categorical sense.) Roughly, this says that Tutte determines magnitude if is determined by and whenever is an edge of that is neither a bridge nor a loop. But I don’t know whether that’s the case; I suspect not.
All in all, I don’t think the magnitude function is likely to be a specialization of the Tutte polynomial, even for connected graphs. In other words, the magnitude function seems to contain extra information about the graph that Tutte doesn’t. But what?
Properties and examples
I’ll now try to convey an idea of how the magnitude function behaves, by way of some basic properties and examples. For comparison, I’ll show the behaviour of the Tutte polynomial alongside.
Disjoint unions Any two graphs and have a disjoint union .
Tutte: .
Magnitude: .
Joins Suppose we have a graph with a distinguished vertex , and another graph with a distinguished vertex . We can form a new graph , the “join”, by first taking then identifying with .
Tutte: .
Magnitude: .
Knows the number of vertices?
Tutte: no, if we’re allowing graphs to have multiple connected-components: see “discrete graphs” below. Yes, if we stick to connected graphs: then the degree of as a polynomial in (with regarded as constant) is .
Magnitude: yes: it’s .
Knows the number of edges?
Tutte: yes: . (Here and later, I’ll use for the set of edges of a graph , and for the set of vertices.)
Magnitude: no, if we’re allowing loops or multiple edges, since adding a loop or a duplicate edge doesn’t change the magnitude. Yes, if we stick to graphs without loops or multiple edges: the coefficient of in the power series expansion of is times the number of edges. In other words, . (See this comment, and the reply to it, below.)
Discrete graphs Let be a discrete graph, that is, one with no edges at all.
Tutte: .
Magnitude: .
Forests Let be a forest, that is, a disjoint union of trees.
Tutte: .
Magnitude: .
Cycles Let be the -cycle:
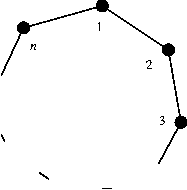
Tutte:
Magnitude: . (Those are the floor and ceiling functions in the denominator.) This naturally splits into two cases. If is even then If is odd then
Complete graphs Let be the complete graph on vertices (that is, every vertex is joined to every other by a single edge).
Tutte: it seems that there is no neat formula for , and that computing it is nontrivial. A single example:
Magnitude: .
Complete bipartite graphs I’ll just do one. Let be this graph:
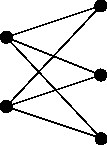
Tutte: .
Magnitude: .
Bull, tadpole, cricket These three graphs all have the same Tutte polynomial and the same magnitude function:
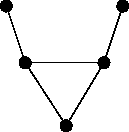
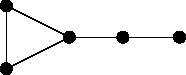
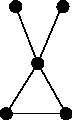
Let be any one of them.
Tutte: .
Magnitude: .
There’s no mystery as to why they all have the same Tutte polynomial. It’s simply because all three graphs are the join of and two copies of the graph consisting of a single edge, and the Tutte polynomial of the join of a bunch of graphs is determined by their individual Tutte polynomials. The same goes for the magnitude functions.
Petersen graph Don Knuth observed that the Petersen graph “serves as a counterexample to many optimistic predictions about what might be true for graphs in general”. So even though I don’t have a prediction to be counterexampled, I thought I’d better check its magnitude function for disturbing behaviour. I’m not disturbed.
Tutte: according to Wikipedia, the Petersen graph has Tutte polynomial
Magnitude: .
Actually, this does defeat a conjecture! Having read the previous examples, you might have wondered whether the coefficients of the magnitude function (when expanded as a power series) always alternate in sign. The Petersen graph shows that they don’t.
Linear codes I’m going to be very sketchy here. (If you want to know more, just say so in the comments.) Let be a finite field. A linear code over is simply a linear subspace of , for some .
Tutte: Every linear code has a Tutte polynomial . (More exactly, the definition of Tutte polynomial extends smoothly from graphs to matroids, and every linear code gives rise to a matroid.) But also, with every linear code is associated an important polynomial called its “weight enumerator”. It’s a fact that the weight enumerator of a code is determined by its Tutte polynomial together with the cardinalities of and .
Magnitude: On the other hand, every linear code can be regarded as a metric space (with the Hamming distance inherited from ), and so has a magnitude function. It’s a fact that the weight enumerator of a code is essentially the same thing as its magnitude function; each determines the other once you know the cardinality of .
So in the case of linear codes, the Tutte polynomial (plus the cardinalities of and ) determines the magnitude function.
Questions
The magnitude function of a graph remains mysterious to me. I have very little intuition for what it means. I understand the magnitude of a metric space moderately well for subspaces of , but metric spaces coming from graphs are about as un-Euclidean as can be.
Here are some questions I’d like answering.
What information can be read off from the magnitude function of a graph?
Is there a useful way to regard the power series expansion of the magnitude function as a generating function? In other words, do the coefficients count something?
It’s consistent with the evidence above that two graphs with the same Tutte polynomial and the same number of vertices have the same magnitude function. Is it true?
It’s consistent with the evidence above that two connected graphs with the same Tutte polynomial have the same magnitude function. Is it true?

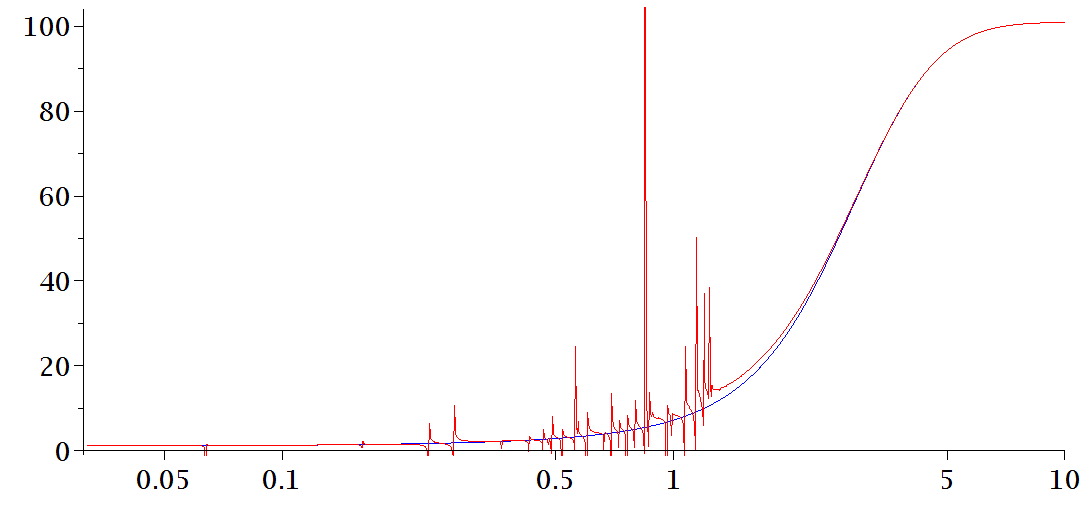
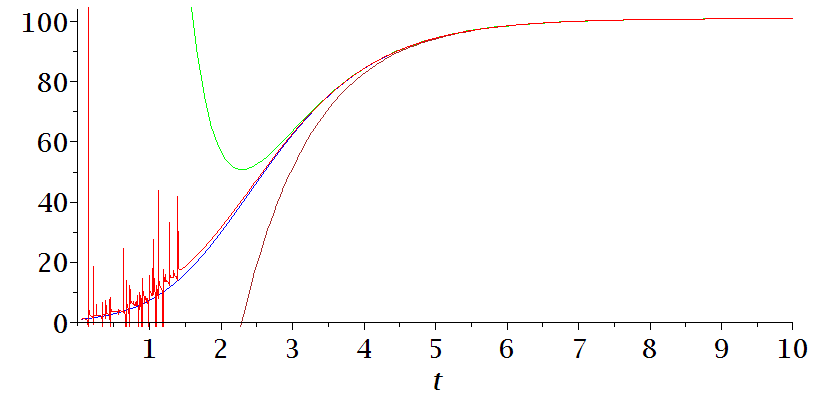
Re: Tutte Polynomials and Magnitude Functions
It occurs to me belatedly that in all the examples I’ve given, the coefficient of in the power series expansion of is times the number of edges.