Whitney Twists
Posted by Tom Leinster
I’m sitting on a plane to Sydney for Category Theory 2013, the major annual gathering of category theorists. At some point I’ll write about the talk I’m giving, which answers the question about ultraproducts posed here and here. But today I’m going to tell you why these two graphs have the same magnitude:
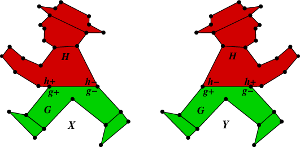
The magnitude of a graph is a somewhat mysterious rational function associated to . It was the subject of vigorous discussion back here, largely provoked by David Speyer and Simon Willerton. I’ll repeat the definition.
So, take a graph , where by “graph” I mean a finite, undirected graph without loops or multiple edges. The distance between two vertices is the minimum length of a path between them (or if there is no path at all). We now define a square matrix over , the field of rational functions in a formal variable . The rows and columns are indexed by the vertices of , and for vertices and , the -entry of is (understood to be if ).
It’s easy to see that the element of is nonzero. (Consider .) Hence is invertible over . The magnitude of is the sum of all the entries of . Thus, the magnitude of a graph is a rational function.
Why might this invariant be interesting? Principally, it’s because it’s a special case of the notion of the magnitude of a metric space, which has proved to be interesting, but has been investigated much more deeply for the kind of spaces that geometers like to think about than for metric spaces arising from graphs.
Last time, I assembled as many examples of graphs and their magnitudes as I could, with the aim of arriving at an intuitive understanding of the magnitude of a graph. The comments thread helped with that. For example, the magnitude of a graph can also be expressed as a power series with integer coefficients, and we discovered an alternating-sum formula for those coefficients. But we’re still in thick murk.
Here’s the main point of this post. Suppose we have a graph , equipped with a pair of distinguished, distinct vertices, and . And suppose we also have another such, . We can make a new graph by gluing to along the two basepoints (deleting the duplicate edge if one is created). In fact, we can do this in two ways:
by gluing to and to , we make a new graph ;
by gluing to and to , we make a new graph .
The graphs and are said to differ by a Whitney twist. For instance, these two graphs differ by a Whitney twist:
In case you can’t see the difference between red and green, the graph is the part from the belt downwards, and the graph is the part from the belt upwards. Since there is a belt, either has an edge between its two basepoints, or does (or both); the picture doesn’t reveal which.
Last time, something extraordinary happened. David Speyer wondered whether graphs differing by a Whitney twist always have the same magnitude. (He wondered this because graphs differing by a Whitney twist always have the same Tutte polynomial.) He tested this idea with an experiment, by getting a computer to see whether it was true for a pair of randomly-generated 10-vertex graphs and . It was.
The magnitudes of David’s graphs and are rational functions of degree 23, whose coefficients are integers of up to five digits, so it’s barely conceivable that they’d be equal by coincidence. And yet, it’s not true in general that graphs differing by a Whitney twist always have the same magnitude!
Simon Willerton gave a counterexample. Here’s a slightly smaller one: the two graphs
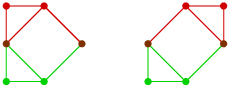
differ by a Whitney twist, but don’t have the same magnitude.
What on earth is going on? Simon suggested a conjecture that would explain the situation. I now have a proof. Here it is:
Theorem Two graphs differing by a Whitney twist have the same magnitude as long as there is an edge between the two gluing points.
Formally, let be a graph, and let and be vertices of joined by an edge. Let be a graph, and let and be vertices of joined by an edge. Then the two graphs
have the same magnitude.
Let’s pause to consider this condition in the statement of the theorem that the two gluing points are joined by an edge. The following are equivalent:
- there’s an edge between the two gluing points of
- either there is an edge between and in or there is an edge between and in
- there’s an edge between the two gluing points of .
Moreover, if (say) there’s an edge between and in , it makes no difference whether there’s one between and in : the new graphs and are the same either way.
The crucial feature of the red and green men is the belt. If it wasn’t there, there’d be no guarantee that their magnitudes were equal.
By the theorem, it’s unsurprising that David got equal magnitudes for a randomly generated Whitney pair , even though it doesn’t happen for all such pairs. Indeed, suppose we do as David did and generate random graphs and by putting an edge between each pair of vertices with probability . Then the probability that either there’s an edge between and in or there’s an edge between and in is . So, doing what David did will give you equal magnitudes at least of the time.
(I’m glad the chance worked out that time— otherwise we’d probably never have discovered all this.)
Why should anyone care about this result? For me, it’s not really graphs themselves that I’m primarily interested in. I care because
Graphs are a bit like convex sets.
Let me explain. A metric space is geodesic if every pair of points can be joined by a path of length : that is, a distance-decreasing map beginning at and ending at . For instance, the geodesic subsets of are exactly the convex sets.
Now let’s consider graphs as metric spaces. All the distances are integers, so for trivial reasons, a graph is never geodesic. But there’s something more interesting to say. Just as a metric space can be seen as a category enriched over , a graph can be seen as a category enriched over . The role played for metric spaces by () is played for graphs by ().
So, a category enriched over should be called geodesic if every pair of objects can be joined by a path of length , where now “path” means a functor (distance-decreasing map) beginning at and ending at . By definition of the metric on a graph, every graph is geodesic in this sense.
From the very beginning of work on the magnitude of metric spaces, there have been difficult conjectures about the magnitude of convex sets. For example, it’s believed that
whenever and are compact convex subsets of such that is also convex. (Here denotes magnitude.)
Despite a lot of work, we don’t seem to be close to a proof. Thus, anything that might provide a clue is welcome. Maybe proving results about the magnitude of graphs will suggest ways to prove analogous results on convex sets.
We need to be cautious, though. The inclusion-exclusion formula does not hold under the hypotheses of the Whitney twist theorem above. That is, and are equal, but they’re not in general equal to . Simon mentioned a counterexample: simply glue two 3-cycles together along an edge.
So is it a bad analogy? No; it’s just that there are several ways to generalize the notion of convexity from subsets of Euclidean space to metric spaces in general. For instance, instead of asking that between each pair of points there exists a geodesic, you might ask that between each pair of points there exists a unique geodesic. For subsets of , both conditions are equivalent to convexity, but for more general metric spaces, one is stricter than the other.
As Mark pointed out, trees always satisfy the analogous condition for graphs. In other words, given vertices and of a tree, distance apart, there is a unique sequence of vertices such that , , and each is joined by an edge to . And indeed, whenever a tree is the union of subtrees and , we do have
This suggests that as far as magnitude is concerned,
Trees are like convex sets
(more so than graphs are). Unfortunately, the proof of the inclusion-exclusion formula for trees is so simple that it’s unlikely to help prove anything about the magnitude of convex sets.
The proof of the Whitney twist theorem for graphs is more involved. I have very little idea how it might be used to advance our understanding of magnitude of convex sets, if indeed it can be. It’s not a conceptual or beautiful proof; it’s just a computation. It also doesn’t reveal what the common magnitude of the new graphs and is, in terms of the old graphs and .
The details I’ll finish with a quick summary of the proof, intended only for the seriously interested.
Sticking with the notation above, we start with and and make new graphs and , differing by a Whitney twist. We assume there’s an edge between and in , and also one between and in . Let be the unique weighting on . We’re going to define a weighting on .
Except at the two gluing points, it’s equal to . To define at those two points, we need some notation. Divide the set of vertices of into three parts, as follows:
The important thing to notice is that and can differ by at most , because of the edge between and . We’ve just carved up according to whether the difference is , or . Of course, we can do the same for , giving sets , and .
The weighting is given at the gluing point of by
Here the first two equalities are by definition, but the last is a lemma, which had better be true in order that the symmetry of the situation is maintained. (Its proof uses the idea of a metric space projecting to a subspace.) There are similar formulas for .
It’s not hard to check that this is a weighting. From the construction of in terms of , it’s then immediate that .

Re: Whitney Twists
One way in which this is so is that, like subsets of Euclidean space, trees are of negative type; a slightly stronger statement is that they embed isometrically in . I wonder if inclusion-exlusion holds for magnitude of graphs which are of negative type or which embed in .