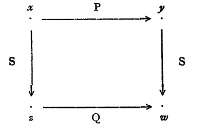
It seems to me that Russell is there just explaining the concept of isomorphism between binary relations. For any
holds. So, he means:
is an isomorphism. So, category-theoretically, the “objects” would be the binary relations and , and would be a morphism.
But the objects at the nodes of Russell’s diagram are relata of and , rather than the relations (i.e., ) themselves. So, it seems to me that aren’t objects in the usual category-theoretic sense; and if so, then this doesn’t seem to be a commutative diagram.
On the other hand, the diagramatic arrows between and express that the atomic formula holds; and this is more like the structural diagram one gives for a relation. So, I think this is diagram in the model-theoretic sense, not category-theoretic sense.
(Maybe, if we wish to thing of as “objects”, we can think of the binary relation as a category: the objects of this category are elements of (the field of ), and a “morphism” holds between when is true. But then, for what Russell is considering, we have two categories, and , and is now a functor between categories!)
Russell was one of first to consider classes of isomorphic relations: in PM, he and Whitehead call them “relation-numbers”, because they generalize the Frege-Russell analysis of cardinals as “class-numbers”, i.e., equivalence classes
of classes under the relation of bijection.
Jeff

Re: The First Commutative Diagram?
Not an earlier example, but, Mac Lane [Concepts and categories in perspective] did suggest that the arrow notation comes from the 1930s/40s.