Searching for a Video Proof of “Seven Trees in One”
Posted by John Baez
James Propp asks:
Can you steer me toward the YouTube video of someone using pebble-moves to prove that is a multiple of , by starting with a single pebble and managing to move it six spaces to the left (or maybe it was to the right?) with moves that replace a pebble at with pebble at each of and , and other moves that do the reverse?
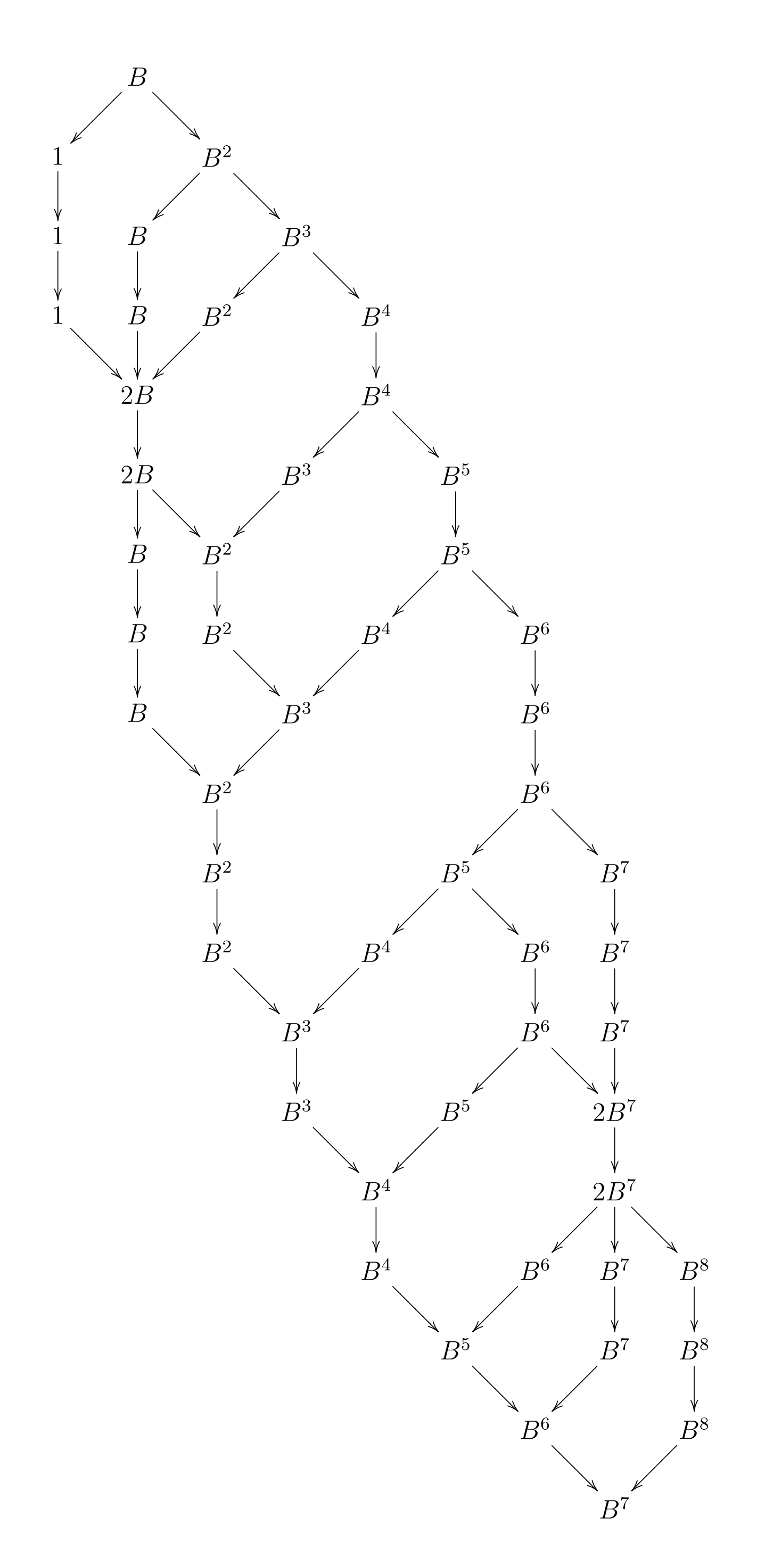
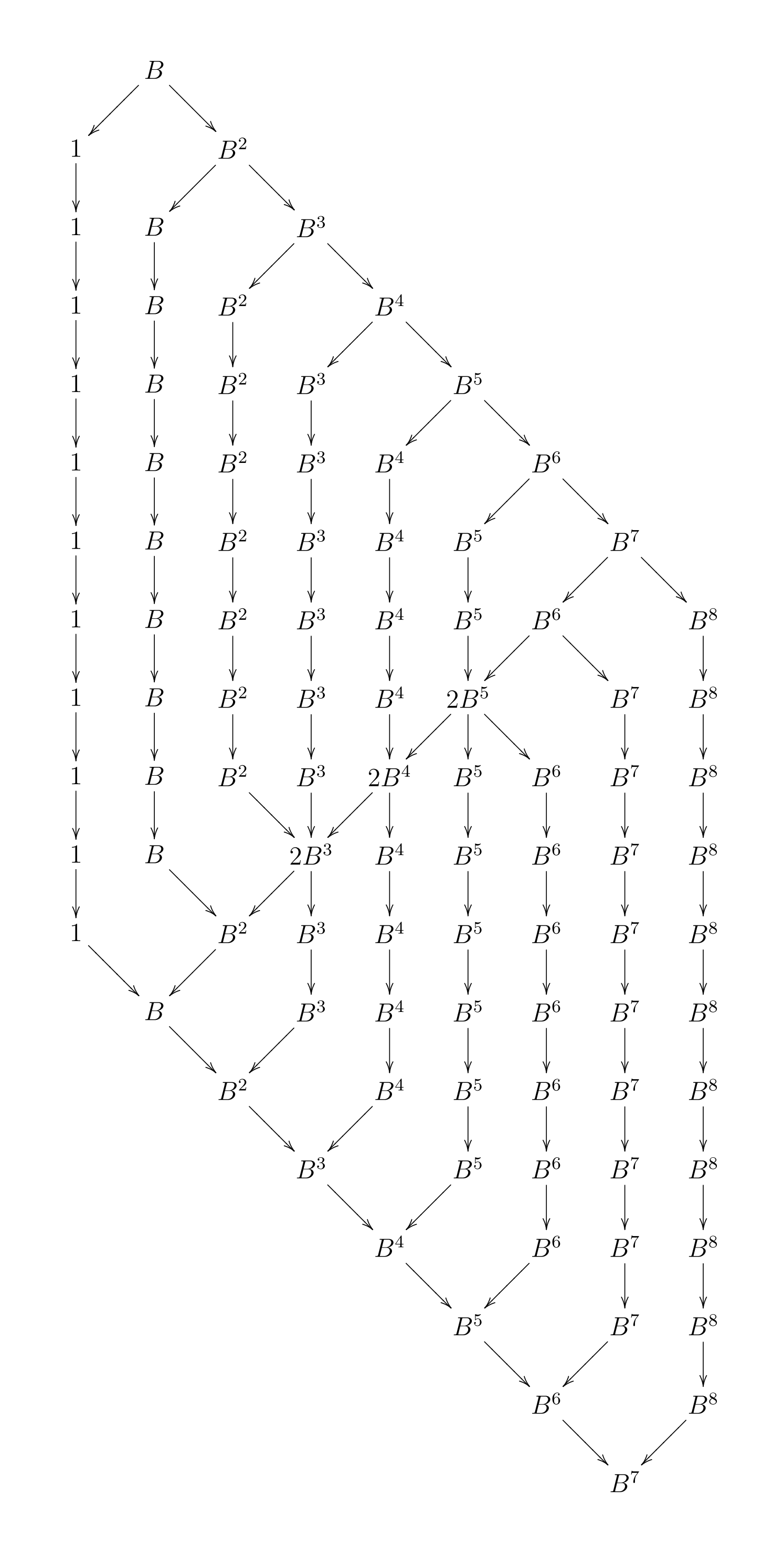
The argument goes back to Andreas Blass’ paper Seven trees in one — he used it to give a nice bijection between the set of binary planar trees and the set of 7-tuples of such trees. The argument was generalized by Robbie Gates and later Marcelo Fiore and Tom Leinster. I discussed it in week202 of This Week’s Finds. But I don’t remember a video proof!
James Propp adds:
I’m pretty sure I learned about it from your This Week’s Finds series, but searching your site on the obvious keywords only led me to Week 202, which has some relevant stuff but doesn’t provide the link I was seeking.
I say pebbles, but I use the term generically to refer to counters, tokens, or chips of any sort.
Here’s a similar argument that proves
This picture is taken from Fiore’s paper Isomorphisms of generic recursive polynomial types:
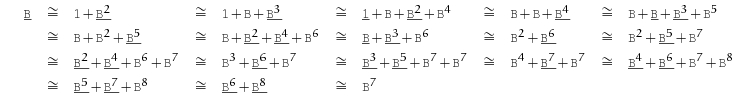
At each step he either replaces by , or the reverse. At each step he underlines the one or two terms that he’s about to replace.
But where’s the video?


Re: Searching for a Video Proof of “Seven Trees in One”
That’ll be me.