Schröder Paths and Reverse Bessel Polynomials
Posted by Simon Willerton
I want to show you a combinatorial interpretation of the reverse Bessel polynomials which I learnt from Alan Sokal. The sequence of reverse Bessel polynomials begins as follows.
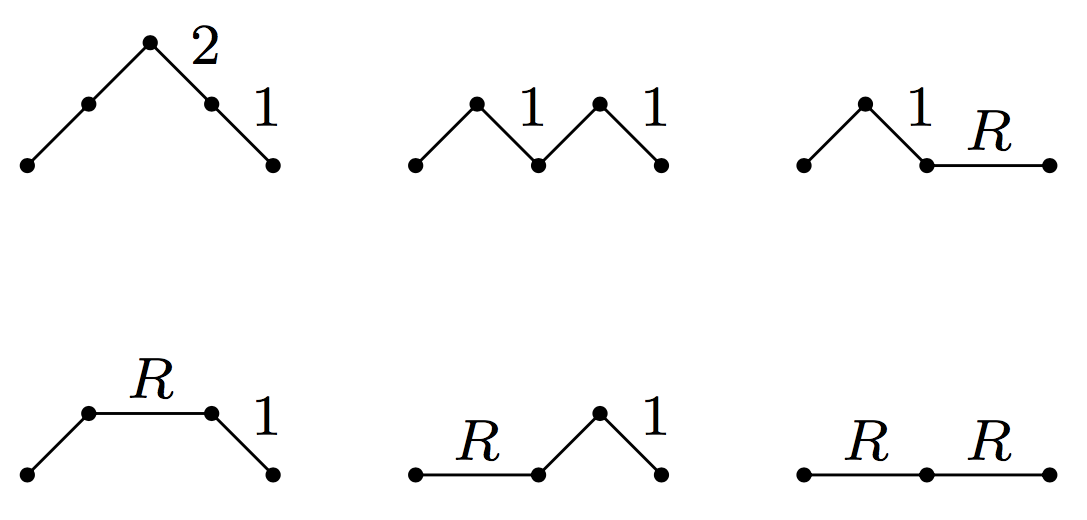
To give you a flavour of the combinatorial interpretation we will prove, you can see that the second reverse Bessel polynomial can be read off the following set of ‘weighted Schröder paths’: multiply the weights together on each path and add up the resulting monomials.
In this post I’ll explain how to prove the general result, using a certain result about weighted Dyck paths that I’ll also prove. At the end I’ll leave some further questions for the budding enumerative combinatorialists amongst you.
These reverse Bessel polynomials have their origins in the theory of Bessel functions, but which I’ve encountered in the theory of magnitude, and they are key to a formula I give for the magnitude of an odd dimensional ball which I have just posted on the arxiv.
In that paper I use the combinatorial expression for these Bessel polynomials to prove facts about the magnitude.
Here, to simplify things slightly, I have used the standard reverse Bessel polynomials whereas in my paper I use a minor variant (see below).
I should add that a very similar expression can be given for the ordinary, unreversed Bessel polynomials; you just need a minor modification to the way the weights on the Schröder paths are defined. I will leave that as an exercise.
The reverse Bessel polynomials
The reverse Bessel polynomials have many properties. In particular they satisfy the recursion relation and satisfies the differential equation There’s an explicit formula:
I’m interested in them because they appear in my formula for the magnitude of odd dimensional balls. To be more precise, in my formula I use the associated Sheffer polynomials, ; they are related by , so the coefficients are the same, but just moved around a bit. These polynomials have a similar but slightly more complicated combinatorial interpretation.
In my paper I prove that the magnitude of the -dimensional ball of radius has the following expression:
As the each polynomial has a path counting interpretation, one can use the rather beautiful Lindström-Gessel-Viennot Lemma to give a path counting interpretation to the determinants in the above formula and find some explicit expression. I will probably blog about this another time. (Fellow host Qiaochu has also blogged about the LGV Lemma.)
Weighted Dyck paths
Before getting on to Bessel polynomials and weighted Schröder paths, we need to look at counting weighted Dyck paths, which are simpler and more classical.
A Dyck path is a path in the lattice which starts at , stays in the upper half plane, ends back on the -axis at and has steps going either diagonally right and up or right and down. The integer is called the length of the path. Let be the set of length Dyck paths.
For each Dyck path , we will weight each edge going right and down, from to by then we will take , the weight of , to be the product of all the weights on its steps. Here are all five weighted Dyck paths of length six.
Famously, the number of Dyck paths of length is given by the th Catalan number; here, however, we are interested in the number of paths weighted by the weighting(!). If we sum over the weights of each of the above diagrams we get . Note that this is . This is a pattern that holds in general.
Theorem A. (Françon and Viennot) The weighted count of length Dyck paths is equal to the double factorial of :
The following is a nice combinatorial proof of this theorem that I found in a survey paper by Callan. (I was only previously aware of a high-tech proof involving continued fractions and a theorem of Gauss.)
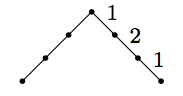
The first thing to note is that the weight of a Dyck path is actually counting something. It is counting the ways of labelling each of the down steps in the diagram by a positive integer less than the height (i.e.~the weight) of that step. We call such a labelling a height labelling. Note that we have no choice of weighting but we often have choice of height labelling. Here’s a height labelled Dyck path.
So the weighted count of Dyck paths of length is precisely the number of height labelled Dyck paths of length .
We are going to consider marked Dyck paths, which just means we single out a specific vertex. A path of length has vertices. Thus
Hence the theorem will follow by induction if we find a bijection
Such a bijection can be constructed in the following way. Given a height labelled Dyck path, remove the left-hand step and the first step that has a label of one on it. On each down step between these two deleted steps decrease the label by one. Now join the two separated parts of the path together and mark the vertex at which they are joined. Here is an example of the process.
Working backwards it is easy to describe the inverse map. And so the theorem is proved.
Schröder paths and reverse Bessel polynomials
In order to give a path theoretic interpretation of reverse Bessel polynomials we will need to use Schröder paths. These are like Dyck paths except we allow a certain kind of flat step.
A Schröder path is a path in the lattice which starts at , stays in the upper half plane, ends back on the -axis at and has steps going either diagonally right and up, diagonally right and down, or horizontally two units to the right. The integer is called the length of the path. Let be the set of all length Schröder paths.
For each Schröder path , we will weight each edge going right and down, from to by and we will weight each flat edge by the indeterminate . Then we will take , the weight of , to be the product of all the weights on its steps.
Here is the picture of all six length four weighted Schröder paths again.
You were asked at the top of this post to check that the sum of the weights equals the second reverse Bessel polynomial. Of course that result generalizes!
The following theorem was shown to me by Alan Sokal, he proved it using continued fractions methods, but these essentially amount to the combinatorial proof I’m about to give.
Theorem B. The weighted count of length Schröder paths is equal to the th reverse Bessel polynomial:
The idea is to observe that you can remove the flat steps from a weighted Schröder path to obtain a weighted Dyck path. If a Schröder path has length and upward steps then it has downward steps and flat steps, so it has a total of steps. This means that there are length Schröder paths with the same underlying length Dyck path (we just choose were to insert the flat steps). Let’s write for the set of Schröder paths of length with upward steps. where the last equality comes from the formula for given at the beginning of the post.
Thus we have the required combinatorial interpretation of the reverse Bessel polynomials.
Further questions
The first question that springs to mind for me is if it is possible to give a bijective proof of Theorem B, similar in style, perhaps (or perhaps not), to the proof given of Theorem A, basically using the recursion relation rather than the explicit formular for them.
The second question would be whether the differential equation has some sort of combinatorial interpretation in terms of paths.
I’m interested to hear if anyone has any thoughts.


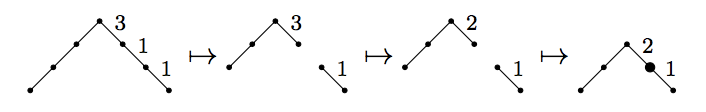
Re: Schröder Paths and Reverse Bessel Polynomials
Interesting post! One thing that comes to mind: have you tried considering the reverse Bessel polynomials in terms of involutions, or equivalently in terms of rooted chord diagrams? There is a simple bijection between height labelled Dyck paths and fixed point free involutions, which I think is easiest to visualize using the representation of involutions by diagrams: scanning a labelled Dyck path from left to right, every NE step introduces a rising arc, while every SE() step introduces a falling arc that closes the th unattached arc. For example, the height labelled Dyck path NE NE NE SE(1) SE(2) SE(1) from your example corresponds to the rooted chord diagram
and to the fixed point free involution (1 4)(2 6)(3 5).
This interpretation extends to weighted Schröder paths by allowing rooted chord diagrams with unattached marked points, hence fixed points of the corresponding involution. For example, under this interpretation the weighted Schröder path NE EE SE(1) corresponds to the involution (1 3)(2), while the path EE NE SE(1) corresponds to the involution (1) (2 3).
I don’t quite see how to interpret the recursion relation for in terms of involutions/chord diagrams. However, consider the formal power series which gathers together all of the reverse Bessel polynomials: Reinterpreting weighted Schröder paths as involutions, Theorem B implies that can be seen as the bivariate generating function counting involutions by total number of cycles () and number of 1-cycles/fixed points (). I wonder whether it might potentially be useful to consider the reparameterization where is the bivariate generating function counting involutions by number of 2-cycles () and 1-cycles () (or equivalently, rooted chord diagrams by number of chords and number of marked points)? In particular, satisfies the functional-differential equation which has the following simple interpretation: starting from the empty rooted chord diagram (1), we can build a larger diagram either by adding an unattached point at the end of a smaller diagram (), or by picking an unattached point of the smaller diagram and closing it with a chord ().