June 20, 2013
The HoTT Book
Posted by Mike Shulman
Many of you have heard murmurings about this book for several months now. I’m happy to report that it’s now out!
At the link you can download electronic versions for screen, ereader, or printer, and order paperback and hardback bound copies at cost from lulu.com. The book is CC BY-SA licensed, which in particular means it will always be freely available.
June 14, 2013
Quasicrystals and the Riemann Hypothesis
Posted by John Baez
Freeman Dyson is a famous physicist who has also dabbled in number theory quite productively. If some random dude said the Riemann Hypothesis was connected to quasicrystals, I’d probably dismiss him as a crank. But when Dyson says this, it’s a lot more interesting. So I’ve been trying to understand his remarks on this. And it’s been productive, in that I’ve learned some interesting things, and I now feel closer to seeing why the Riemann Hypothesis is a natural and important conjecture.
But still, I could use a lot of help: I don’t have much time for number theory, and a few pointers from experts could keep me from going down dead ends.
The Selected Papers Network
Posted by John Baez
Here it is at last: the Selected Papers Network. Given that social networks already exist, all we need for truly open scientific communication is a convention on a consistent set of tags and IDs for discussing papers. Christopher Lee, in bioinformatics at UCLA, has developed software that makes this work. Try it out!
What’s cool about this system is that it’s federated. Instead of locking up your comments within its own website—the “walled garden” strategy followed by many other service—it explicitly shares these data in a way that people not on the Selected Papers Network can easily see. Any other service can see and use them too.
June 7, 2013
G2 and the Rolling Ball
Posted by John Huerta
I just returned from a month at Hong Kong University, visiting James Fullwood, an algebraic geometer who likes to think about the mathematics of string theory. There, I gave a colloquium on G2 and the rolling ball, a paper John Baez and I wrote that is due to appear in Transactions of the AMS. This project began over a decade ago in conversations between John and Jim Dolan, later continued between Jim and me. Though Jim opted not to be a coauthor, his insights were crucial.
I would like to tell you about this paper, but I’ll warm up with a puzzle—one you’ve seen in several guises if you’ve read John Baez’s posts about this paper, but well-worth revisiting.
Puzzle: Roll a ball of unit radius on a fixed ball of radius , being careful not to let your ball slip or twist as you roll it. Suppose you roll along a great circle from the North Pole to the South Pole and back to the start at the North. How many turns did the ball make as it rolled?
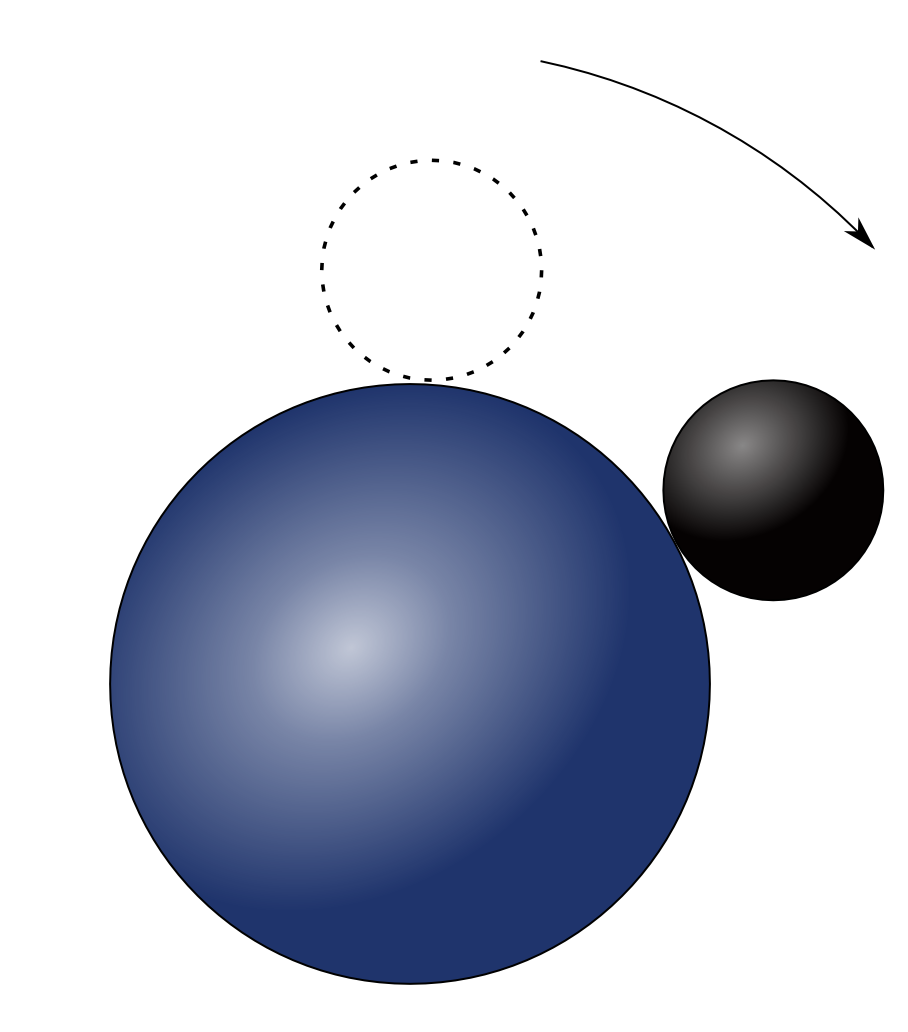
Here’s a variant of this puzzle you can work out very concretely: for , roll one coin around another of the same kind, without slipping, and count the number of times the rolling coin turns.
Below the fold, I’ll give you the answer, and I’ll also tell you about something amazing that happens when , bringing in the exceptional Lie group and a funky 8-dimensional number system called the split octonions.
June 3, 2013
Torsors and Enriched Categories
Posted by Simon Willerton
In another instalment of my occasional series on ‘Things you didn’t realise were enriched categories (unless you’re an expert!)’ I want to talk about torsors and how they can be considered enriched categories where the enriching category is a group, considered as a discrete monoidal category.
I’ll start off by telling you what a torsor is and then explain how it can be thought of as having something like a ‘group-valued distance’ and how this relates to enriched category theory.
June 1, 2013
Welcome, Emily
Posted by Tom Leinster
I’m happy to announce that Emily Riehl has joined us as a host at the Café. Emily is based at Harvard, and you can deduce some of her interests from the many guest posts she has written for us before:
Welcome, Emily!
 Posts with this logo use
Posts with this logo use 















