November 26, 2014
Grothendieck’s Activism And What It Says About The World
Posted by Tom Leinster
Mathematician Ivar Ekeland has an excellent, thoughtful, article at Mediapart, reflecting on the second phase of Grothendieck’s adult life.
The article is perhaps more about mathematics and its place in the world than about Grothendieck specifically. Among the questions Ekeland asks: What exactly are you, as a researcher, looking for? What are your intellectual boundaries? How do you justify spending your life on mathematics? Why was Grothendieck a less successful activist than mathematician? And what does that say about the world?
Below the fold is my translation of selected passages from Ekeland’s article, which is in French. Feel free to suggest improvements to the translation.
November 23, 2014
Integral Octonions (Part 9)
Posted by John Baez
Now let’s talk about building the Leech lattice from integral octonions!
The Leech lattice is a marvelous thing. Here are three ways to define it:
Take a bunch of balls of radius one in 24 dimensions. Get as many balls to touch a single ball as you possibly can. Then, get as many balls to touch these as you possibly can. Go on like this forever. Unlike in 3 dimensions, you have no real choice about how to do this: the balls will inevitably be centered at points of the Leech lattice.
Take disks of radius one in the plane and pack them in the densest possible lattice arrangement. Use this pattern to form a layer of balls in 3 dimensions. Stack layers like this on top of each other, pushing them down to get the densest possible lattice packing of 3d balls. Use this pattern to form a layer of balls in 4 dimensions! Stack layers like this on top of each other, pushing them down to get the densest possible lattice packing of 4d balls. Repeat this until you get to 24 dimensions. There will be some choices — but no matter how you make these choices, you’ll inevitably be led to the Leech lattice.
Up to isometry, the Leech lattice is the unique even unimodular lattice in 24 dimensions whose shortest nonzero vectors have length 2.
Since the Leech lattice lives in 24 dimensions and octonions live in 8, we should try to describe points in the Leech lattice using triples of octonions.
November 22, 2014
Barbie on Monads
Posted by Tom Leinster
November 19, 2014
General Topology Notes
Posted by Tom Leinster
This semester, I’ve had the pleasure of teaching a 4th year undergraduate course on topology. One of the great things about it has been the students, who are a really engaged and gifted bunch. I’ve possibly enjoyed teaching this course more than any I’ve taught before.
Another pleasure is that, having nearly reached the end of term, I find that I’ve written a complete set of notes for the course. (There’s also an introductory lecture and a set of problem sheets.) Comments welcome! It’s the first year I’ve taught this, so presumably I’ll be using some version of these notes for the next couple of years.
The course begins with the definition of topological space and takes it from there, going through standard constructions and then compactness and connectedness. It seems to me that Year 4 is pretty late to be teaching this stuff (though Scottish university students typically start a year younger than those in England or Wales, so it’s roughly equivalent to 3rd year south of the border). But on the plus side, the students had already done a good amount on metric spaces, including compactness and connectedness, and that softened up the ground nicely.
November 18, 2014
The Kan Extension Seminar in the Notices
Posted by Tom Leinster
Emily has a two-page article in the latest issue of the Notices of the American Mathematical Society, describing her experience of setting up and running the Kan extension seminar. In my opinion, the seminar was an exciting innovation for both this blog and education at large. It also resulted in some excellent posts. Go read it!

November 16, 2014
Jaynes on Mathematical Courtesy
Posted by Tom Leinster
In the last years of his life, fierce Bayesian Edwin Jaynes was working on a large book published posthumously as Probability Theory: The Logic of Science (2003). Jaynes was a lively writer. In an appendix on “Mathematical formalities and style”, he really let rip, railing against modern mathematical style. Here’s a sample:
Nowadays, if you introduce a variable without repeating the incantation that it is in some set or ‘space’ , you are accused of dealing with an undefined problem. If you differentiate a function without first having stated that it is differentiable, you are accused of lack of rigor. If you note that your function has some special property natural to the application, you are accused of lack of generality. In other words, every statement you make will receive the discourteous interpretation.
Discuss.
November 15, 2014
Integral Octonions (Part 8)
Posted by John Baez
This time I’d like to summarize some work I did in the comments last time, egged on by a mysterious entity who goes by the name of ‘Metatron’.
As you probably know, there’s an archangel named Metatron who appears in apocryphal Old Testament texts such as the Second Book of Enoch. These texts rank Metatron second only to YHWH himself. I don’t think the Metatron posting comments here is the same guy. However, it’s a good name for someone interested in lattices and geometry, since there’s a variant of the Cabbalistic Tree of Life called Metatron’s Cube, which looks like this:
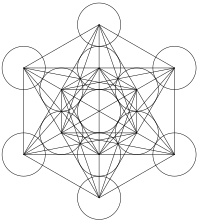
This design includes within it the root system, a 2d projection of a stellated octahedron, and a perspective drawing of a hypercube.
Anyway, there are lattices in 26 and 27 dimensions that play rather tantalizing and mysterious roles in bosonic string theory. Metatron challenged me to find octonionic descriptions of them. I tried.
November 5, 2014
Integral Octonions (Part 7)
Posted by John Baez
Greg Egan and I have been thinking about Lorentzian lattices, and he just proved something nice about : it’s the lattice of self-adjoint matrices with integral octonions as entries!
This might be known already, but I’ve never seen it anywhere. So, let me show you the proof. But first, let me remind you why it matters.
If you missed the earlier parts of this series, you can see polished-up versions on my website:
-
Part 1: integral octonions and the Coxeter group E10. Also available here on the n-Category Café.

-
Part 2 - the integral octonions, 11d supergravity, and cosmological billiards. Also available here on the n-Category Café.
-
Part 3 - the 240 smallest integer octonions, also known as the E8 root polytope, and their connection to exceptional objects in mathematics. Also available here on the n-Category Café.

-
Part 4 - faces of the E8 root polytope. Also available here on the n-Category Café.
-
Part 5 - Dynkin diagrams and the geometry of the E8 root polytope. Also available here on the n-Category Café.
-
Part 6 - how to multiply octonions, and the Cayley integral octonions. Also available here on the n-Category Café.
 Posts with this logo use
Posts with this logo use 















