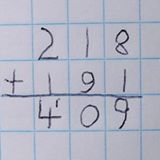July 30, 2013
Keep Calm and Carry One
Posted by Tom Leinster
Here’s a short diversion. My friend and mathematical big sister Audrey Tan, who’s a professional maths tutor in her native New Zealand, has been waging a campaign for the NZ government to return column addition to the early primary school curriculum. Primary school seems to be ages 5–12, so I guess “early primary” means kids aged 5–8 or so.
What’s column addition? It’s the way I, and probably you, add up natural numbers with pen and paper:
(Demonstration here, on the off-chance that you have no idea what this picture means.) For reasons I don’t understand, the NZ government has decided that this isn’t worth teaching in the first few years. Audrey thinks that’s madness, and is trying hard to put it right.
(Since this has caused some confusion, let me clarify: in NZ, column addition is taught, but much later than you might expect — not until the kids are about ten and have, supposedly, already digested the concept of place value.)
I’m curious to know: is this the method you learned when you were very little? Or did you learn to add some other way?
July 29, 2013
Integral Octonions (Part 3)
Posted by John Baez
You’ve probably heard about E8. It’s the name of several closely connected structures: a Lie group, a Lie algebra, a Coxeter group and a lattice in 8 dimensions.
The lattice in 8 dimensions is what concerns me most right now, because this lattice underlies the Cayley integers: the ‘integral octonions’ that are the theme of this little series. You can think of the integral octonions as giving the lattice a multiplication making it into a nonassociative division ring.
But before getting into the multiplicative aspects, it’s good to be thoroughly familiar with the additive and geometrical aspects. So, let’s start with a few calculations with and get to know it as a lattice in 8-dimensional Euclidean space. Then let’s think a bit about how it’s related to the Lie algebra , and the smaller Lie algebras and .
All this stuff is fun in its own right, but it will also come in handy later if this series progresses as I’m imagining. Part 1 and Part 2 were very sketchy. But ideally, I’d like to show you the algebra and geometry related to Cayley integers very vividly, and for that we need some details.
July 28, 2013
Minhyong Kim in The Reasoner
Posted by David Corfield
I recently interviewed Minhyong Kim for Kent’s in-house magazine, The Reasoner, where it now appears in the August. As before with Urs, beware the abrupt transition to the following article.
Reading this,
The work that occupies me most right now, arithmetic homotopy theory, concerns itself very much with arithmetic moduli spaces that are similar in nature and construction to moduli spaces of solutions to the Yang-Mills equation,
one could dream of connections to Urs’ work.
Cohomology Detects Failures of Classical Mathematics
Posted by Mike Shulman
Ordinarily I try to avoid cross-posting between here and the Homotopy Type Theory blog, but this remark seems probably of interest to the crowd here as well. After my recent post there about how to define cohomology in HoTT, Zhen Lin kindly pointed me to a very nice paper of Andreas Blass called Cohomology detects failures of the axiom of choice. A main result of this paper is that the following two statements are equivalent (over ZF):
- The axiom of choice.
- For any discrete set and any (not necessarily abelian) group , the cohomology vanishes.
The fact that discrete spaces have no higher cohomology is “obvious” in classical algebraic topology, but this shows that if we want to do homotopy theory “constructively” then we need to give up that expectation. In this post I want to explain one of Blass’s proofs from a geometric point of view, and then consider what cohomology has to say about the law of excluded middle.
July 25, 2013
Integral Octonions (Part 2)
Posted by John Baez
Last time I said that sitting inside the octonions there’s a subset called the ‘Cayley integers’
closed under addition and multiplication. Geometrically speaking, this is a rescaled copy of the lattice sitting inside 8-dimensional Euclidean space. And I said this gives rise to a discrete subgroup
where is a Lie group isomorphic to , the identity component of the Lorentz group of 10-dimensional Minkowski spacetime. Just as the more familiar group acts as symmetries of the hyperbolic plane, acts as symmetries of a 9-dimensional hyperbolic space.
Now I’d like to say a bit about what this does for us. In particular, how it relates 11-dimensional supergravity to the game of billiards!
I would also like to explain in vivid detail what the Cayley integers and the action of ‘look like’—along with some lower-dimensional examples that arise from other kinds of integers inside the real numbers, complex numbers and quaternions. That would force me to learn some interesting things. But I think it’s better to start by zipping through the big picture, and then returning to details later if I have time.
July 24, 2013
Higher Compactness
Posted by Mike Shulman
Higher category theorists enjoy categorifying stuff. That word can mean lots of things, but one thing it can mean is to take some familiar 1-category, embed it naturally into a higher category, and then try to extend some of the appropriate theory. And one of the threads in topos theory is to do this with topology, where we start with the 1-category of topological spaces.
July 23, 2013
Integral Octonions (Part 1)
Posted by John Baez
This is not particularly about -categories, but it’s related — somehow — to John Huerta’s work on division algebras and Lie n-superalgebras, which are the -categorified versions of Lie superalgebras, which in turn are the supersymmetric versions of Lie algebras.
You see, some of the most exciting Lie -superalgebras are those extending the Lie algebra of the Lorentz group in 10 or 11 dimensions, and these can be built using the octonions. The reason is that 10d Minkowski spacetime can be identified with the space consisting of hermitian matrices with octonions as entries. Thanks to this, the corresponding Lorentz group, the identity component of , can be identified with . It is somewhat tricky to define , because the octonions are nonassociative, but it can be done, and this caps off a very nice sequence of isomorphisms:
Now I’d like I describe how this interacts with a further marvelous fact: the existence of ‘octonionic integers’.
July 10, 2013
A Weighted Limits Proof of Monadicity
Posted by Emily Riehl
Since the 1970s, it has been known that the Eilenberg-Moore object (EM-object) associated with a monad in a 2-category can be characterized as a weighted limit. An element of the limit of a Set-valued diagram can be thought of as a cone over that diagram. Similarly, in the case of a monad in Cat, an object of this weighted limit, more commonly called an algebra for the monad, is exactly a cone over the monad diagram whose shape is described by the weight.
Using the weighted limits formalism, EM-objects in a 2-category are defined representably. It follows that the monadicity theorem characterizing EM-objects and their monadic adjunction can be deduced representably from the monadicity theorem in Cat. Despite this fact, I want to give a direct proof of the 2-categorical monadicity theorem to illustrate that a suitable reinterpretation of Beck’s proof is “all in the weights.” To begin, we’ll use weighted limits to characterize the monadic adjunction. It follows immediately that any adjunction inducing the same monad has a comparison map to the monadic adjunction. Inspecting the weights, we observe that the monadic forgetful functor is conservative. We also show that any object in the EM-object is the colimit of a canonical diagram, itself described by a weighted limit, and the monadic forgetful functor preserves these colimits. If the domain of the comparison map admits certain colimits, this map has a left adjoint. If the forgetful functor is conservative, then the comparison adjunction is an adjoint equivalence.
The point of all this is that the 2-functors defining these weights can be interpreted as simplicial functors. The same discussion, with only minimal modifications, then gives a (formal!) proof of the monadicity theorem for homotopy coherent adjunctions of quasi-categories. I’ll be speaking about this in Sydney this week and Warsaw later this month. This is joint work with Dominic Verity.
Synthetic ∞-Groupoid Theory
Posted by Mike Shulman
This week I’m at the 2013 International Category Theory conference in Syndey, Australia, along with our co-hosts Tom and Emily (and a bunch of other people (-: ). There’s a lot of interesting stuff being said that I don’t have time to write about right now, but I thought I would go ahead and post the slides for my own talk that I gave yesterday, since I’ve had one or two requests:
- Homotopy type theory: towards Grothendieck’s dream (pdf slides)
July 8, 2013
The First Commutative Diagram?
Posted by Tom Leinster
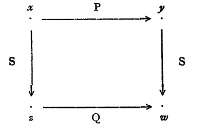
At lunch today at Category Theory 2013 in Sydney, a bunch of us were talking about the mathematical work of Bertrand Russell, and I remembered this:
It’s from Russell’s 1919 book Introduction to Mathematical Philosophy, and it’s essentially a commutative square in the category of sets and relations, although the notation is very slightly different from how we’d do it now. Click on the image to see the whole page.
I was very surprised to see a commutative diagram from 1919. This was more than twenty years before the birth of category theory. Indeed, I’m not sure that the arrow notation for mappings was commonplace back then. Does anyone know of an earlier example of a commutative diagram in print?
July 7, 2013
Whitney Twists
Posted by Tom Leinster
I’m sitting on a plane to Sydney for Category Theory 2013, the major annual gathering of category theorists. At some point I’ll write about the talk I’m giving, which answers the question about ultraproducts posed here and here. But today I’m going to tell you why these two graphs have the same magnitude:
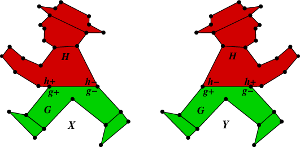
The magnitude of a graph is a somewhat mysterious rational function associated to . It was the subject of vigorous discussion back here, largely provoked by David Speyer and Simon Willerton. I’ll repeat the definition.
 Posts with this logo use
Posts with this logo use