March 14, 2015
Split Octonions and the Rolling Ball
Posted by John Baez
You may enjoy these webpages:
because they explain a nice example of the Erlangen Program more tersely — and I hope more simply — than before, with the help of some animations made by Geoffrey Dixon using WebGL. You can actually get a ball to roll in way that illustrates the incidence geometry associated to the exceptional Lie group !
Abstract. Understanding exceptional Lie groups as the symmetry groups of more familiar objects is a fascinating challenge. The compact form of the smallest exceptional Lie group, , is the symmetry group of an 8-dimensional nonassociative algebra called the octonions. However, another form of this group arises as symmetries of a simple problem in classical mechanics! The space of configurations of a ball rolling on another ball without slipping or twisting defines a manifold where the tangent space of each point is equipped with a 2-dimensional subspace describing the allowed infinitesimal motions. Under certain special conditions, the split real form of acts as symmetries. We can understand this using the quaternions together with an 8-dimensional algebra called the ‘split octonions’. The rolling ball picture makes the geometry associated to quite vivid. This is joint work with James Dolan and John Huerta, with animations created by Geoffrey Dixon.
March 11, 2015
A Scale-Dependent Notion of Dimension for Metric Spaces (Part 1)
Posted by Simon Willerton
Consider the following shape that we are zooming into and out of. What dimension would you say it was?
At small scales (or when it is very far away) it appears as a point, so seems zero-dimensional. At bigger scales it appears to be a line, so seems one-dimensional. At even bigger scales it appears to have breadth as well as length, so seems two-dimensional. Then, finally, at very large scales it appears to be made from many widely separated points, so seems zero-dimensional again.
We arrive at an important observation:
The perceived dimension varies with the scale at which the shape is viewed.
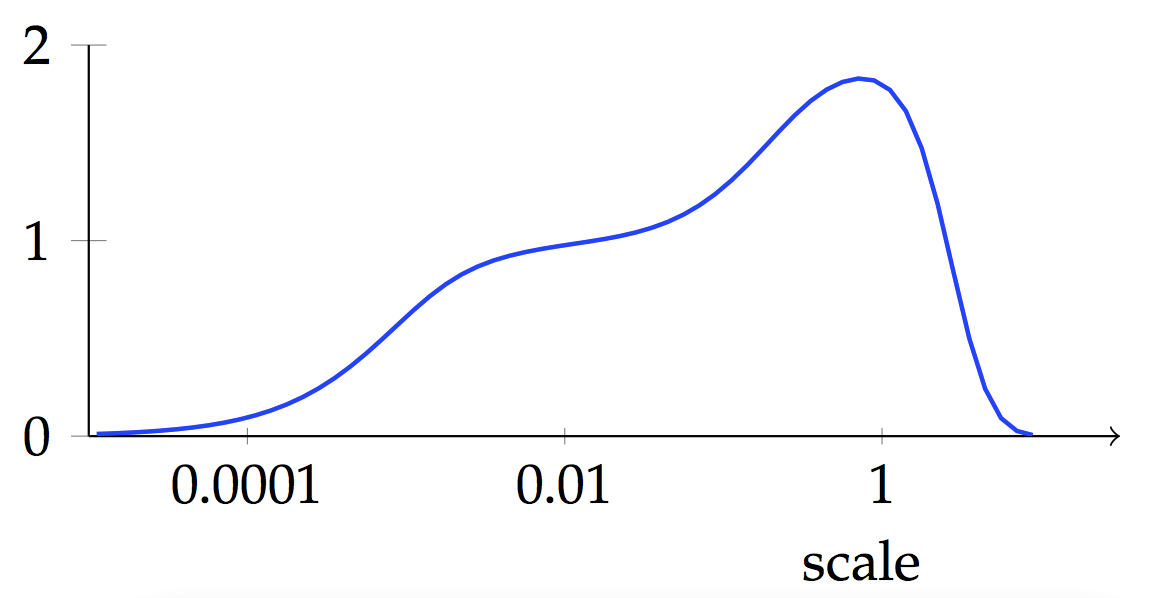
Here is a graph of my attempt to capture this perceived notion of dimension mathematically.
Hopefully you can see that, moving from the left, you start off at zero, then move into a region where the function takes value around one, then briefly moves up to two then drops down to zero again.
The ‘shape’ that we are zooming into above is actually a grid of points as that’s all my computer could handle easily in making the above picture. If I’d had a much bigger computer and used say points then I would have got something that more obviously had both a one-dimensional and two-dimensional regime.
In this post I want to explain how this idea of dimension comes about. It relies on a notion of ‘size’ of metric spaces, for instance, you could use Tom’s notion of magnitude, but the above picture uses my notion of -spread.
I have mentioned this idea before at the Café in the post on my spread paper, but I wanted to expand on it somewhat.
March 9, 2015
HITs and the Erlangen Program
Posted by Mike Shulman
Last week I had a minor epiphany, which I would like to share. If it holds up, it’ll probably end up somewhere in my chapter for Landry’s book.
I was fortunate during my formal education to have the opportunity to take a fair number of physics classes in addition to mathematics. Over that time I was introduced to tensors (more specifically, tensor fields on manifolds) several times in a row: first in special relativity, then in differential geometry, and then again in general relativity and Riemannian geometry.
During all those classes, I remember noticing that mathematicians and physicists tended to speak about tensors in different ways. To a mathematician, a tensor (field) was a global geometric object associated to a manifold; upon choosing a local chart it could be expressed using local coordinates, but fundamentally it was a geometric thing. By contrast, physicists tended to talk about a tensor as a collection of coordinates labeled by indices, with its “tensorial” nature encoded in how those coordinates transformed upon changing coordinates.
(To be sure, most physicists nowadays are aware of the mathematician’s perspective, and many even use it. But I still got the sense that they found it easier, or at least expected that we students would find it easier, to think in coordinates.)
Here is my epiphany: the symbiosis between these two viewpoints on tensors is closely related to the symbiosis between HITs and univalence in homotopy type theory. I will now explain…
March 5, 2015
Mathematics Without Apologies
Posted by David Corfield
Since I had reviewed the manuscript for Princeton University Press eighteen months ago, this week I received my complementary copy of Mathematics Without Apologies by Michael Harris.
Michael, as most people here will know, is a number theorist whose successes include, with Richard Taylor, the proof of the local Langlands conjecture for the general linear group in characteristic 0. But alongside being a prize-winning mathematician, he also likes to think hard about the nature of mathematics. He spoke at a conference I co-organised, Two Streams in the Philosophy of Mathematics, and I’ve met up with him on a number of other occasions, including the Delphi meeting with John. He’s extremely well placed then to give an account of the life of a current mathematician with, as suggested by the book’s subtitle, Portrait of a problematic vocation, all its peculiarities.
I’ll be re-reading the book once term is over, and say more then, but for now those wanting to find out more can read a Q&A with the author, and drafts of some chapters available here. Michael has also set up an associated blog, named after the book.
 Posts with this logo use
Posts with this logo use