January 30, 2010
This Week’s Finds in Mathematical Physics (Week 292)
Posted by John Baez
In week292 of This Week’s Finds, learn about Henry Paynter’s “bond graphs” — diagrams that engineers use to model systems made of mechanical, electronic, and/or hydraulic components: springs, gears, levers, pulleys, pumps, pipes, motors, resistors, capacitors, inductors, transformers, amplifiers, and so on. And learn how different classes of systems like this call for different kinds of mathematics: symplectic geometry, complex analysis, and even a bit of Hodge theory.
January 25, 2010
6th Workshop on Categories, Logic and Foundations of Physics
Posted by Urs Schreiber
Readers of this blog will know about the workshop series on Categories, Logic and Foundations of Physics, that Bob Coecke and Andreas Döring have been running since two years ago. It has become tradition that we report on this here a bit on the Café as witnessed by previous entries
Categories, Logic and Phyiscs in London
Categories, Logic and Phyiscs in London, II
Categories, Logic and Foundations of Physics in Oxford
on the first three events. John had also reported on
Categories, Quanta and Concepts at the Perimeter Institute
which sounds alike, in title and organizers, but was maybe not part of the official series. We seem to have skipped the announcement of parts 4 and 5, for some reason. But now here is number 6:
Categories, Logic and Foundations of Physics (CLP 6),
Oxford University Computing Laboratory
Tuesday, 9th March 2010, 12:00 - 18:20.
(website)
January 24, 2010
Equivariant Stable Homotopy Theory
Posted by Mike Shulman
Over the past week (at least), Urs and I and some others have been trying to understand equivariant stable homotopy theory from a higher-categorical point of view, with some help from experts like Peter May, John Greenlees, and Megan Shulman. Unfortunately, the online part of the discussion has been taking place simultaneously in two different, hard-to-find, and arguably inappropriate places, namely the nForum and the comments on a mostly unrelated thread. So I thought I would give it a thread of its own, along with with an easier-to-read introduction and summary to bring new people into the discussion.
Before we dive in, let me say that equivariant things can be tricky and involve lots of traps for the categorically-minded. (At least, there are a lot of things that trapped me.) If you need some motivation to spur you on and keep you going, note that the recent proof of the Kervaire invariant one problem involved the tools of equivariant homotopy theory in very important ways. So this stuff really is good for something.
January 23, 2010
This Week’s Finds in Mathematical Physics (Week 291)
Posted by John Baez
In week291 of This Week’s Finds, learn about Carlos Simpson’s new book. Listen to a crab canon on a Möbius strip. See how the Mandelbrot set mimics infinitely many Julia sets:

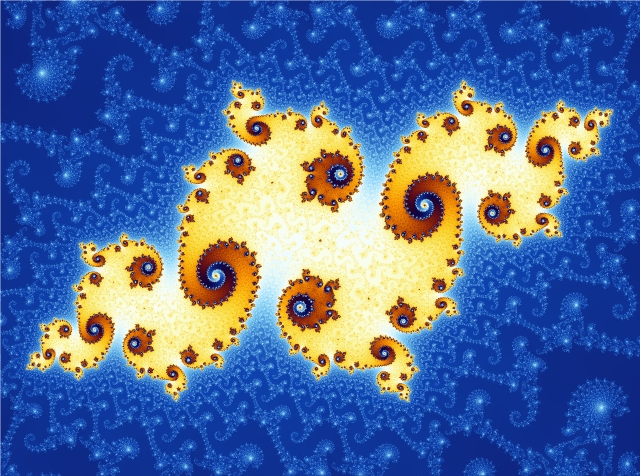
Then, continue our exploration of analogies between electrical circuits and other physical systems. This time we’ll meet the most important 2-ports and 3-ports — and get a tiny taste of Poincaré duality for electrical circuits.
January 18, 2010
The Sacred and the Profane
Posted by David Corfield
The categories mailing list recently engaged in some soul-searching as to why category theory remains such a well-kept secret and why its wonders are not better known. Many people proposed theories to explain this, while others were quick to deny the premise, pointing out that it is no longer a secret, as the mainstream work of Voevodsky, Lurie, and many others bears witness. I wonder, though, if this was quite the point at stake.
When I met up with Minhyong Kim before Christmas he made the very interesting remark that there’s a difference between treating some system of mathematics in a ‘sacred’ way and in a ‘profane’ way. This distinction was introduced by Dirk van Dalen in the Preface to his Logic and Structure:
Logic appears in a ‘sacred’ and in a ‘profane’ form; the sacred form is dominant in proof theory, the profane form in model theory. The phenomenon is not unfamiliar, one observes this dichotomy also in other areas, e.g. set theory and recursion theory. Some early catastrophes such as the discovery of the set theoretical paradoxes or the definability paradoxes make us treat a subject for some time with the utmost awe and diffidence. Sooner or later, however, people start to treat the matter in a more free and easy way. Being raised in the ‘sacred’ tradition my first encounter with the profane tradition was something like a culture shock. Hartley Rogers introduced me to a more relaxed world of logic by his example of teaching recursion theory to mathematicians as if it were just an ordinary course in, say, linear algebra or algebraic topology. In the course of time I have come to accept this viewpoint as the didactically sound one: before going into esoteric niceties one should develop a certain feeling for the subject and obtain a reasonable amount of plain working knowledge. For this reason this introductory text sets out in the profane vein and tends towards the sacred only at the end. (p. V)
January 16, 2010
This Week’s Finds in Mathematical Physics (Week 290)
Posted by John Baez
In week290 of This Week’s Finds, ponder the number of seconds in a week — and the number of inches in a mile. Read about categorification in analysis. Learn more about analogies between different kinds of physical systems, and meet the five most popular 1-ports: resistances, capacitances, inertances, effort sources and flow sources. And take stock of where we stand in our tour of rational homotopy theory!
January 14, 2010
Going to Singapore
Posted by John Baez
Yay! My leave was finally approved!
It’s official!
F and the Shibboleth
Posted by Tom Leinster
Marcelo Fiore and I have just sent in what I hope is the final version of our paper An abstract characterization of Thompson’s group , to be published in Semigroup Forum.
When we wrote the paper I thought it was all about , and in a sense it is. But through a long and difficult refereeing process, involving a couple of other journals, I came to realize that in social terms it was more about a shibboleth. I’ll explain each of these things, and the shibboleth, in turn.
January 8, 2010
This Week’s Finds in Mathematical Physics (Week 289)
Posted by John Baez
In week289 of This Week’s Finds, hear the latest news about . Then, continue exploring the grand analogy between different kinds of physics. We’ll get into a bit of thermodynamics — and chemistry, too! Finally, learn more about rational homotopy theory, this time entering the world of “differential graded Lie algebras”, which lets us use Lie theory to study topological spaces.
Quasicoherent ∞ -Stacks
Posted by Urs Schreiber
This is to tie up a loose end in our discussion of Ben-Zvi/Francis/Nadler geometric -function theory and Baez/Dolan/Trimble “groupoidification”.
Using a central observation in Lurie’s Deformation Theory one can see how both these approaches are special examples of a very general-abstract-nonsense theory of -linear algebra on -vector bundles and -quasicoherent sheaves in arbitrary (“derived”) -stack -toposes:
the notion of module is controled by the tangent -category of the underlying site, that of quasicoherent module/-vector bundle simply by homs into its classifying -functor.
For Ben-Zvi/Francis/Nadler this shows manifestly, I think, that nothing in their article really depends on the fact that the underlying site is chosen to be that of duals of simplicial rings. It could be any -site. For Baez/Dolan/Trimble it suggests the right way to fix the linearity: their setup is that controlled by the tangent -category of itself and where they (secretly) use the codomain bifibration over this, one should use the fiberwise stabilized codomain fibration.
See -vector bundle for a discussion of what I have in mind.
What I am saying here is likely very obvious to somebody out there. I have my suspicions. But it looks like such a nice fundamental fact, that this deserves to be highlighted, and be it in a blog entry. It is just a matter of putting 1 and 1 together. The two central observations are this:
Looking for Compatible Structure
Posted by David Corfield
Here’s a little puzzle for you. Imagine you wanted to set out to find an ordered set with lots of compatible algebraic structure. You’ve just been reading Michiel Hazewinkel’s Niceness Theorems, where he writes
These ruminations started with the observation that it is difficult for, say, an arbitrary algebra to carry additional compatible structure. To do so it must be nice, i.e., as an algebra be regular (not in the technical sense of this word), homogeneous, everywhere the same,… It is for instance very difficult to construct an object that has addition, multiplication and exponentiation, all compatible in the expected ways.
So you have the idea that you’re after a homogeneous order. Where to find one? Well, you’ve also just been reading about the Fraïssé limit construction, and so know that these limits possess homogeneity in spades. So you look up the Fraïssé limit for linear orders, and wait expectantly for opportunities to impose compatible algebraic structure. You won’t be disappointed. Not only does the limit support an addition and a multiplication, it turns out that we can impose an ordered field structure. We have, in fact, arrived at the rationals, the smallest ordered field.
January 6, 2010
What You’re Doing is Good for You
Posted by Tom Leinster
Like a foodstuff that’s both delicious and nutritious, making your articles open access is not only morally upstanding, but also gets you cited more:
Yassine Gragouri et al, Self-selected or mandated, open access increases citation impact for higher quality research.
Unfortunately it’s hidden behind a paywall. No, of course it’s not; it’s on the arXiv. The title pretty much says it all (and probably won’t come as a surprise). The ‘self-selected or mandated’ part is explained in the abstract…
The Math of Environmental Sustainability at Harvey Mudd
Posted by John Baez
Ever wonder what mathematicians can do to help solve the environmental problems facing all of us? I do. Maybe this will help:
- 2010 Harvey Mudd College Mathematics Conference on the Mathematics of Environmental Sustainability and Green Technology, Harvey Mudd, Claremont, California, Friday–Saturday, January 29–30, 2010. Organized by Rachel Levy.
January 4, 2010
Coenergy
Posted by John Baez
It’s Newton’s birthday! Google has a nice homepage today, which shows an apple dropping…
In honor of Sir Isaac, I thought I’d ask a question that’s related to classical mechanics: what’s coenergy?
Generalized Multicategories
Posted by Mike Shulman
Geoff Cruttwell and I have just finished an improved version of our paper “A unified framework for generalized multicategories,” which can be found here. Although the main purpose of the paper is, as the title says, to describe a framework which unifies the many existing approaches to generalized multicategories, we deliberately started out from basics so that it would also be suitable as an introduction to the subject. So whether or not you’ve ever encountered generalized multicategories before, if you have a chance to look over the paper, we’d appreciate any feedback. It’s a little long, but not as long as it looks, since a lot of space is taken up by diagrams.
(Coincidentally, the timing of this post is quite good; this paper is another example of the importance of double categories, proarrow equipments, and lax functors. The notion of “representability” for generalized multicategories is also closely related to the “algebraic/non-algebraic” dichotomy under discussion here.)
January 1, 2010
This Week’s Finds in Mathematical Physics (Week 288)
Posted by John Baez
Happy New Year!

In week288 of This Week’s Finds, start learning about an enormous set of analogies linking electrical circuits, classical mechanics, hydraulics, thermodynamics and chemistry. And continue learning about rational homotopy theory! This time we’ll dig deeper into the ‘commutative cochain problem’, and see why the ordinary cup product on singular cochains is almost but not quite commutative.
 Posts with this logo use
Posts with this logo use 















