The n-Category Café

To explain $F$, I’ll begin by quoting our paper.

In the 1960s Richard Thompson discovered three groups, now called $F$, $T$ and $V$, with remarkable properties. The group $F$, in particular, is one of those mathematical objects that appears in many diverse contexts and has been rediscovered repeatedly.

Informally, $F$ is the group of all automorphisms of the interval $[0, 1]$ — if all you knew about $[0, 1]$ was that it was isomorphic to $[0, 2]$.

Here $[0, 2]$ should be viewed as two copies of $[0, 1]$ stuck end-to-end (sometimes written $[0, 1] \vee [0, 1]$). So, we know that there’s an isomorphism $$\alpha: [0, 2] \to [0, 1],$$ and that’s all we know about $[0, 1]$. From $\alpha$, we can build some nontrivial automorphisms of $[0, 1]$, that is, some nontrivial elements of $F$. Here’s one:

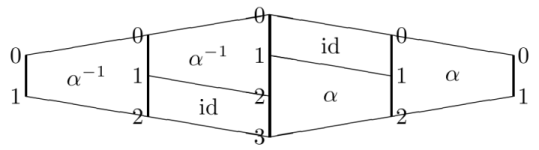
It does no harm to assume that $\alpha$ is division by $2$, in which case we can redraw this element as a graph:

Another way to redraw the first picture is by thinning it out, so that each wedge-shaped $\alpha$ or $\alpha^{-1}$ becomes a skinny Y-shape:

This is a rather simple, combinatorial way of representing an element of the group — but if you work with these pictures, it’s not so obvious what the group operation is. Points if you can figure it out, and bonus points if you can see what it’s got to do with the bicategory of spans.

Aside  What about Thompson’s other groups, $T$ and $V$? Well, I more or less said that $F$ is the automorphism group of $[0, 1]$ considered as a self-similar space — by which I mean, equipped with the obvious isomorphism $[0, 1] \vee [0, 1] \to [0, 1]$. (As a mere set, the interval has a massive automorphism group; as a topological space or ordered set, its automorphism group is smaller; as a self-similar space, it’s smaller still.) In the same sense, $V$ is the automorphism group of the Cantor set, and $T$ the automorphism group of the circle, both considered as self-similar spaces in a natural way. I’d love to make these statements precise, so that $F$, $T$ and $V$ were literally automorphism groups of these three objects in a category of self-similar spaces; but at present, I can’t.

Here’s our theorem. Given a monoidal category $\mathbf{M}$, an idempotent object in $\mathbf{M}$ is an object $M$ together with an isomorphism $\mu: M \otimes M \to M$. For example, if $\mathbf{M}$ is the monoidal category of sets with cartesian product, an idempotent object is a set $M$ equipped with a bijection $M \times M \to M$: a Jónsson–Tarski algebra.

Theorem  Let $\mathbf{A}$ be the monoidal category freely generated by an idempotent object $(A, \alpha)$. Then $Aut_{\mathbf{A}} (A) \cong F$.

For example, the composite map $$A \stackrel{\alpha^{-1}}{\to} A \otimes A \stackrel{\alpha^{-1} \otimes id}{\to} A \otimes A \otimes A \stackrel{id \otimes \alpha}{\to} A \otimes A \stackrel{\alpha^{-1}}{\to} A$$ is an automorphism of $A$ in $\mathbf{A}$, and represents the same element of $F$ as shown in the pictures above.

All the objects of $\mathbf{A}$ are isomorphic except for the unit object $I$, which doesn’t really do much. We might as well have used the free ‘semigroupal category’ (monoidal category without unit) instead. It makes no difference, but since monoidal categories are what people usually think about, that’s what we used. Perhaps we should have submitted our paper to Semigroup Forum’s great rival, Monoid Forum.

Aside  If you’re an expert on Thompson’s groups, you may at this point be snorting and muttering to yourself:

But this has been known since Thompson and Higman!

Or, you may be snorting and muttering to yourself:

But this has been known since Freyd and Heller!

And indeed, there are old results of Thompson, Higman, and Freyd and Heller that bear a tantalizing resemblance to the theorem above. But they are not the same! And, more importantly, no one has yet managed to find a simple or direct deduction of our result from one of these older ones, or vice versa. In other words, no one has succeeded in taking advantage of the tantalizing resemblances. Take that as a challenge!

I hope that the theorem comes as no surprise, given the earlier (informal) description of $F$. At least, I hope it wasn’t surprising if you’re comfortable with phrases such as ‘the monoidal category freely generated by an idempotent object’. And this brings us to the shibboleth.

Someone — John Baez, I think — taught me how to spot a fake knot theorist. (You can never be too careful.) Simply ask them to draw a trefoil. If they hesitate in the slightest, they’re faking it. Actually, this will only catch really bad fakes, but in some weak sense it’s a shibboleth, a mark of identity, or at the very least, something that any professional can do.

The point I want to make is that for category theory, the ability to throw around phrases of the form

the free such-and-such category containing a such-and-such

is something like the ability to draw a trefoil without hesitation. Of course, this comparison isn’t entirely serious: one of these skills is much more meaningful than the other. But there is something serious here. While there are plenty of people who are fluent in quite sophisticated category- and topos-speak, it seems to me that outside the smallish group for whom category theory is a central research interest, not many people are comfortable with phrases of this form. And that’s a shame. Maybe there was a time when only hard-core algebraists understood phrases of the form

the group freely generated by such-and-such subject to such-and-such.

If so, we’re now in the same social situation, but categorified.

Let me explain what phrases of this kind mean. I’ll use an example:

the free monoidal category containing a monoid.

Another way to say it would be:

the monoidal category freely generated by a monoid.

When you first hear a phrase like this, you might respond ‘the monoidal category freely generated by which monoid?’ But that’s a kind of grammatical misunderstanding.

To understand this phrase, first you have to know (of course) what a monoidal category is. I’ll assume this. For my purposes, monoidal categories will be strict. Then, crucially, you have to know that it makes sense to talk about monoids in a monoidal category. I’ll assume this too.

Now, there’s an informal description of the monoidal category $\mathbf{A} = (\mathbf{A}, \otimes, I)$ freely generated by a monoid. It contains a monoid, whose underlying object I’ll call $A$ and whose multiplication and unit I’ll call $$\mu: A \otimes A \to A,             \eta: I \to A.$$ Since $\mathbf{A}$ is a monoidal category, it has objects $A^{\otimes n}$ for all $n \geq 0$ (with $A^{\otimes 0} = I$). There’s nothing forcing $\mathbf{A}$ to have any other objects, and since it’s supposed to be ‘free’, it doesn’t have any other objects. Similarly, there’s nothing forcing any two of these objects $I, A, A^{\otimes 2}, A^{\otimes 3}, \ldots$ to be equal, and it’s ‘free’, so they’re not equal. The maps in $\mathbf{A}$ are built up from $\mu$, $\eta$ and identities using composition and $\otimes$; they only satisfy whatever equations they have to satisfy in order for $\mathbf{A}$ to be a monoidal category and $(A, \mu, \eta)$ to be a monoid in it.

(In fact, there’s a simple, explicit description of $\mathbf{A}$: the maps $A^{\otimes m} \to A^{\otimes n}$ correspond to order-preserving maps $\{ 1, \ldots, m\} \to \{1, \ldots, n\}$. Hence $\mathbf{A}$ is equivalent to the category of finite totally ordered sets.)

Formally, the monoidal category freely generated by a monoid can be characterized as follows. The characterization relies on one more piece of knowledge: that given any monoidal functor $F: \mathbf{M} \to \mathbf{N}$ and any monoid $(M, \mu, \eta)$ in $\mathbf{M}$, you get a monoid $(FM, F\mu, F\eta)$ in $\mathbf{N}$. (Monoidal functors, like monoidal categories, are taken to be strict here.)

Definition  A monoidal category freely generated by a monoid is a monoidal category $\mathbf{A}$ together with a monoid $(A, \mu, \eta)$ in $\mathbf{A}$, satisfying the following universal property:

for any monoidal category $\mathbf{M}$ and monoid $(M, \mu', \eta')$ in $\mathbf{M}$, there is a unique monoidal functor $F: \mathbf{A} \to \mathbf{M}$ such that $(FA, F\mu, F\eta) = (M, \mu', \eta')$.

The universal property determines $\mathbf{A}$ and $(A, \mu, \eta)$ uniquely, up to isomorphism.

Both the informal and formal descriptions are supposed to remind you of presentations of groups, modules etc. Informally, the group presented by a bunch of generators and relations is obtained by starting with the generators, forming all the terms that you have to form in order for it to be a group, then imposing the relations. Formally, this group is characterized by a universal property rather similar to the one above. What we’ve done is categorification:

• sets-with-structure have become categories-with-structure
• structure-preserving functions have become structure-preserving functors
• generating elements have become generating objects and arrows

etc.

Once you’ve digested this idea, a whole lot of powerful mathematical statements become easily accessible. For example:

• The braided monoidal category freely generated by an object is the sequence $(B_n)_{n \geq 0}$ of Artin braid groups. (More precisely: this category has objects $I, A, A^{\otimes 2}, \ldots$, the automorphism group of $A^{\otimes n}$ is $B_n$, and there are no other morphisms.)
• The free category with finite products containing a group, ring, etc., is the Lawvere theory of groups, rings, etc.
• The free topos containing a group, ring, etc., is the classifying topos for groups, rings, etc. (‘Free topos’ has to be understood with respect to the inverse image part of geometric morphisms, as explained here.)
• The free symmetric monoidal category on a commutative Frobenius algebra is the category of 1-dimensional smooth oriented manifolds and diffeomorphism classes of 2-dimensional cobordisms. This is a strong form of the classification theorem for 2-dimensional TQFTs, as explained nicely in Joachim Kock’s book.
• The free monoidal category containing an object $A$ and an isomorphism $A \otimes A \to A$ is equivalent to the groupoid $1 + F$, where $1$ is the terminal groupoid, $+$ is disjoint union of groupoids, and $F$ is Thompson’s group.

The joy of it is that you can use these descriptions as definitions. Need to tell someone what ‘the Lawvere theory of groups’ is? Just tell them it’s the free finite-product category containing a group. Need to tell them what Thompson’s group $F$ is? Just tell them to form the free monoidal category on an object $A$ and an isomorphism $A \otimes A \to A$; then $F$ is the automorphism group of $A$.