Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

June 29, 2015

What is a Reedy Category?

Posted by Mike Shulman

I’ve just posted the following preprint, which has apparently quite little to do with homotopy type theory.

The notion of Reedy category is common and useful in homotopy theory; but from a category-theoretic point of view it is odd-looking. This paper suggests a category-theoretic understanding of Reedy categories, which I find more satisfying than any other I’ve seen.

Continue reading “What is a Reedy Category?” …
Posted at 6:33 PM UTC | Permalink | Followups (20)

Feynman’s Fabulous Formula

Posted by Simon Willerton

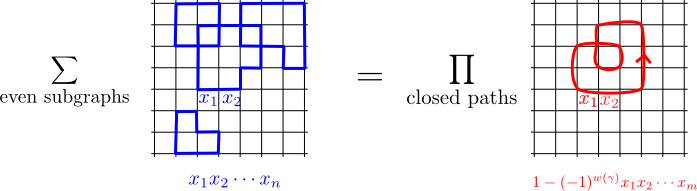
Guest post by Bruce Bartlett.

There is a beautiful formula at the heart of the Ising model; a formula emblematic of all of quantum field theory. Feynman, the king of diagrammatic expansions, recognized its importance, and distilled it down to the following combinatorial-geometric statement. He didn’t prove it though — but Sherman did.

Feynman’s formula. Let GG be a planar finite graph, with each edge ee regarded as a formal variable denoted x ex_e. Then the following two polynomials are equal:

∑ H⊆ evenGx(H)=∏ [γ→]∈P(G)(1−(−1) w[γ→]x[γ→])\displaystyle \sum_{H \subseteq_{even} G} x(H) = \prod_{[\vec{\gamma}] \in P(G)} \left(1 - (-1)^{w[\vec{\gamma}]} x[\vec{\gamma}]\right)

pic

I will explain this formula and its history below. Then I’ll explain a beautiful generalization of it to arbitrary finite graphs, expressed in a form given by Cimasoni.

Continue reading “Feynman’s Fabulous Formula” …
Posted at 7:47 AM UTC | Permalink | Followups (26)

June 21, 2015

What’s so HoTT about Formalization?

Posted by Mike Shulman

In my last post I promised to follow up by explaining something about the relationship between homotopy type theory (HoTT) and computer formalization. (I’m getting tired of writing “publicity”, so this will probably be my last post for a while in this vein — for which I expect that some readers will be as grateful as I).

As a potential foundation for mathematics, HoTT/UF is a formal system existing at the same level as set theory (ZFC) and first-order logic: it’s a collection of rules for manipulating syntax, into which we can encode most or all of mathematics. No such formal system requires computer formalization, and conversely any such system can be used for computer formalization. For example, the HoTT Book was intentionally written to make the point that HoTT can be done without a computer, while the Mizar project has formalized huge amounts of mathematics in a ZFC-like system.

Why, then, does HoTT/UF seem so closely connected to computer formalization? Why do the overwhelming majority of publications in HoTT/UF come with computer formalizations, when such is still the exception rather than the rule in mathematics as a whole? And why are so many of the people working on HoTT/UF computer scientists or advocates of computer formalization?

Continue reading “What’s so HoTT about Formalization?” …
Posted at 6:47 AM UTC | Permalink | Followups (12)

June 12, 2015

Carnap and the Invariance of Logical Truth

Posted by David Corfield

I see Steve Awodey has a paper just out Carnap and the invariance of logical truth. We briefy discussed this idea in the context of Mautner’s 1946 article back here.

Steve ends the article by portraying homotopy type theory as following in the same tradition, but now where invariance is under homotopy equivalence. I wonder if we’ll see some variant of the model/theory duality he and Forssell found in the case of HoTT.

Posted at 12:09 PM UTC | Permalink | Followups (2)

June 9, 2015

Semigroup Puzzles

Posted by John Baez

Suppose you have a semigroup: that is, a set with an associative product. Also suppose that

xyx=x x y x = x

for all xx and all yy.

Puzzle 1. Prove that

xyz=xz x y z = x z

for all x,yx,y and zz.

Puzzle 2. Prove that

xx=x x x = x

for all xx.

Continue reading “Semigroup Puzzles” …
Posted at 2:30 PM UTC | Permalink | Followups (43)