Feynman’s Fabulous Formula
Posted by Simon Willerton
Guest post by Bruce Bartlett.
There is a beautiful formula at the heart of the Ising model; a formula emblematic of all of quantum field theory. Feynman, the king of diagrammatic expansions, recognized its importance, and distilled it down to the following combinatorial-geometric statement. He didn’t prove it though — but Sherman did.
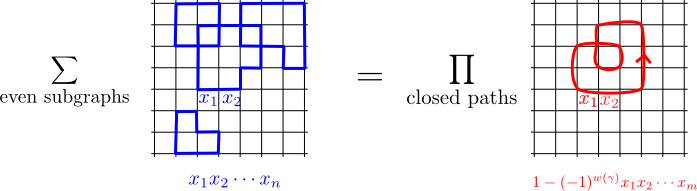
Feynman’s formula. Let be a planar finite graph, with each edge regarded as a formal variable denoted . Then the following two polynomials are equal:
I will explain this formula and its history below. Then I’ll explain a beautiful generalization of it to arbitrary finite graphs, expressed in a form given by Cimasoni.
What the formula says
The left hand side of Feynman’s formula is a sum over all even subgraphs of , including the empty subgraph. An even subgraph is one which has an even number of half-edges emanating from each vertex. For each even subgraph , we multiply the variables of all the edges together to form . So, the left hand side is a polynomial with integer coefficients in the variables .
The right hand side is a product over all , where is the set of all prime, reduced, unoriented, closed paths in . That’s a bit subtle, so let me define it carefully. Firstly, our graph is not oriented. But, by an oriented edge , I mean an unoriented edge equipped with an orientation. An oriented closed path is a word of composable oriented edges ; we consider up to cyclic ordering of the edges. The oriented closed path is called called reduced if it never backtracks, that is, if no oriented edge is immediately followed by the oriented edge . The oriented closed path is called prime if, when viewed as a cyclic word, it cannot be expressed as the product of a given oriented closed path for any . Note that the oriented closed path is reduced (resp. prime) if and only if is. It therefore makes sense to talk about prime reduced unoriented closed paths , by which we mean simply an equivalence class .
Suppose is embedded in the plane, so that each edge forms a smooth curve. Then given an oriented closed path , we can compute the winding number of the tangent vector along the curve. We need to fix a convention about what happens at vertices, where we pass from the tangent vector at the target of to the tangent vector at the source of . We choose to rotate into by the angle less than in absolute value.
Note that , so that its parity makes sense for unoriented paths. Finally, by we simply mean the product of all the variables for along .
The product on the right hand side is infinite, since is infinite in general (we will shortly do some examples). But, we regard the product as a formal power series in the terms , each of which only receives finitely many contributions (there are only finitely many paths of a given length), so the right hand side is a well-defined formal power series.
Examples
Let’s do some examples, taken from Sherman. Suppose is a graph with one vertex and one edge :
Write . There are two even subgraphs — the empty one, and itself. So the sum over even subgraphs gives . There is only a single closed path in , namely , with odd winding number, so the sum over paths also gives . Hooray!
Now let’s consider a graph with two loops:
There are 4 even subgraphs, and the left hand side of the formula is . Now let’s count closed paths . There are infinitely many; here is a table. Let and be the counterclockwise oriented versions of and . If we multiply out the terms the right hand side gives In order for this to equal we will need some miraculous cancellation in the higher powers to occur! And indeed this is what happens. The minus signs from the winding numbers conspire to cancel the remaining terms. Even in this simple example, the mechanism is not obvious — but it does happen.
Pondering the meaning of the formula
Let’s ponder the formula. Why do I say it is so beautiful?
Well, the left hand side is combinatorial — it has only to do with the abstract graph , having the property that it is embeddable in the plane (this property can be abstractly encoded via Kuratowski’s theorem). The right hand side is geometric — we fix some embedding of in the plane, and then compute winding numbers of tangent vectors! So, the formula expresses a combinatorial (or topological) property of the graph in terms of geometry.
Ok… but why is this formula emblematic of all of quantum field theory? Well, summing over all loops is what the path integral in quantum mechanics is all about. (See Witten’s IAS lectures on the Dirac index on manifolds, for example.) Note that the quantum mechanics path integral has recently been made rigorous in the work of Baer and Pfaffle, as well as Fine and Sawin.
Also, I think the formula has overtones of the linked-cluster theorem in perturbative quantum field theory, which relates the generating function for all Feynman diagrams (similar to the even subgraphs) to the generating function for connected Feynman diagrams (similar to the closed paths). You can see why Feynman was interested!
History of the formula
One beautiful way of computing the partition function in the Ising model, due to Kac and Ward, is to express it as a square root of a certain determinant. (I hope to explain this next time.) To do this though, they needed a “topological theorem” about planar graphs. Their theorem was actually false in general, as shown by Sherman. It was Feynman who reformulated it in the above form. From Mark Kac’s autobiography (clip):
The two-dimensional case for so-called nearest neighbour interactions was solved by Lars Onsager in 1944. Onsager’s solution, a veritable tour de force of mathematical ingenuity and inventiveness, uncovered a number of suprising features and started a series of investigations which continue to this day. The solution was difficult to understand and George Uhlenbeck urged me to try to simplify it. “Make it human” was the way he put it …. At the Institute [for Advanced Studies at Princeton] I met John C. Ward … we succeeded in rederiving Onsager’s result. Our success was in large measure due to knowing the answer; we were, in fact, guided by this knowledge. But our solution turned out to be incomplete… it took several years and the effort of several people before the gap in the derivation was filled. Even Feynman got into the act. He attended two lectures I gave in 1952 at Caltech and came up with the clearest and sharpest formulation of what was needed to fill the gap. The only time I have ever seen Feynman take notes was during the two lectures. Usually, he is miles ahead of the speaker but following combinatorial arguments is difficult for all mortals.
Feynman’s formula for general graphs
Every finite graph can be embedded in some closed oriented surface of high enough genus. So there should be a generalization of the formula to all finite graphs, not just planar ones. But on the right hand side of the formula, how do we compute the winding number of a closed path on a general surface? The answer, in the formulation of Cimasoni, is beautiful: we should sum over spin structures on the surface, each weighted by their Arf invariant!
Generalized Feynman formula. Let be a finite graph of genus . Then the following two polynomials are equal:
The point is that a spin structure on can be represented as a nonzero vector field on minus a finite set of points, with even index around these points. (Of course, a nonzero vector field on the whole of won’t exist, except on the torus. That is why we need these points.) So, we can measure the winding number of a closed path with respect to this background vector field .
The first version of this generalized Feynman formula was obtained by Loebl, in the case where all vertices have degree 2 or 4, and using the notion of Sherman rotation numbers instead of spin structures (see also Loebl and Somberg). In independent work, Cimasoni formulated it differently using the language of spin structures and Arf invariants, and proved it in the slightly more general case of general graphs, though his proof is not a direct one. Also, in unpublished work, Masbaum and Loebl found a direct combinatorial argument (in the style of Sherman’s proof of the planar case) to prove this general, spin-structures version.
Last thoughts
I find the generalized Feynman’s formula to be very beautiful. The left hand side is completely combinatorial / topological, manifestly only depending on . The right hand picks some embedding of the graph in a surface, and is very geometric, referring to high-brow things such as spin structures and Arf invariants! Who knew that there was such an elegant geometric theorem lurking behing arbitrary finite graphs?
Moreover, it is all part of a beautiful collection of ideas relating the Ising model to the free fermion conformal field theory. (Indeed, the appearance of spin structures and winding numbers is telling us we are dealing with fermions.) Of course, physicists knew this for ages, but it hasn’t been clear to mathematicians exactly what they meant :-)
But in recent times, mathematicians are making this all precise, and beautiful geometry is emerging, like the above formula. There’s even a Fields medal in the mix. It’s all about discrete complex analysis, spinors on Riemann surfaces, the discrete Dirac equation, isomonodromic deformation of flat connections, heat kernels, conformal invariance, Pfaffians, and other amazing things (here is a recent expository talk of mine). I hope to explain some of this story next time.


 and
and 
Re: Feynman’s Fabulous Formula
That’s clearly a fabulous formula. But why does the formula hold? Sometimes this kind of combinatorial formula can be seen as counting the same thing in two different ways. Do you know of anything similar going on here?