June 29, 2010
Categorification and Topological Invariants in Luminy
Posted by Alexander Hoffnung
Yesterday began the petit groupe de travail with the title “Categorification and Topological Invariants” at the Centre International des Rencontres Mathématiques (CIRM) in Luminy. This week-long meeting is meant to be both introductory as well as an opportunity to explore interesting questions in the fields of interest of the various participants. So far this seems to be going quite well.
I will give a little diary below the fold, and I will try to fill in some of what I hear or say in the talks as comments.
June 28, 2010
Dutch Geometry and Quantum Theory Conference 2010
Posted by Urs Schreiber
The fourth annual conference of the Dutch Geometry and Quantum Theory cluster takes place this week in Nijmegen:
Inevitability in Mathematics
Posted by David Corfield
I’m just back from a conference in Nancy – From Practice to Results in Logic and Mathematics. As you see from the abstract, I was speaking about the inevitability of certain things appearing in mathematics: entities, facts, theories, ideas. We had a discussion of the related robustness a while ago.
Someone posed me the question of the inevitability of Lie groups. Forgetting worries about anachronism, what is our very best account of why the Lie group construct was going to be reached by a mathematics as sophisticated as ours? Can we do better than
Groups are interesting as models of symmetry, manifolds are interesting as models of smooth space, therefore group objects in the category of manifolds will be interesting as models of smoothly varying symmetry?
The other side of the coin is to think of constructs which are arbitrary and contingent. If someone had told me about hypergroups and hyperrings, where instead of a binary operation sending a pair of elements to a single element, it takes them to a nonempty set of elements, I would have imagined that they would have been good candidates for arbitrariness. When, however, you find that Alain Connes is using them in search of an absolute arithmetic, you naturally take notice:
We show that the trace formula interpretation of the explicit formulas expresses the counting function of the hypothetical curve associated to the Riemann zeta function, as an intersection number involving the scaling action on the adele class space. Then, we discuss the algebraic structure of the adele class space both as a monoid and as a hyperring. We construct an extension of the hyperfield of signs, which is the hyperfield analogue of the semifield of tropical geometry, admitting a one parameter group of automorphisms fixing . Finally, we develop function theory over and we show how to recover the field of real numbers from a purely algebraic construction, as the function theory over .
I wonder whether Durov’s generalized rings are related.
June 25, 2010
Alan Carey’s 60th Birthday Conference
Posted by Urs Schreiber
This week at MPI Bonn is (or has been) taking place a conference in honor of Alan Carey’s 60th birthday. on “noncommutative geometry and index theory, statistical models, geometric issues in quantum field theory. Hamiltonian anomalies and bundle n-gerbes”.
I missed most of it, but am on my way now for the last day at least.
June 21, 2010
Exact Squares
Posted by Mike Shulman
One of the slogans of -category theory is that most theorems of ordinary 1-category theory generalize to the -world if you’re careful enough with how you phrase them. One might hope that that the proofs of these theorems could likewise be generalized, and this is sometimes the case, but many of the more complex tools of -category theory don’t have much of a counterpart in the 1-categorical world, such as the study of various types of anodyne morphisms of simplicial sets.
Recently I’ve been talking, reading, and writing about derivators, which I view as a way of working with -categories that is less dependent on technical details of any particular definition of -categories, is more closely connected to familiar techniques of 1-category theory, and may hopefully be easier, in some absolute sense, than working directly with -categories. However, generalizing an argument from 1-categories to derivators does usually still require rephrasing it a bit, because derivators are based around an approach to 1-categorical limits and colimits that isn’t that well known in many circles – the theory of exact squares of categories. So in this post I want to talk about the calculus of exact squares, mainly from a purely 1-categorical viewpoint, but I’ll add some remarks at the end about how easy it is to generalize the arguments to derivators.
June 20, 2010
2010 Octoberfest
Posted by John Baez
Canada has traditionally been a great place for category theory… and the tradition lives on:
- Category Theory “Octoberfest” Workshop, October 23-24, 2010, Dalhousie University, Halifax, Canada, organized by Dorette Pronk and Peter Selinger.
June 18, 2010
Workshop on Music, Patterns and Mathematics
Posted by Simon Willerton
Some of you might be interested in the following meeting.
This summer, the Institute for Music in Human and Social Development (IMHSD), in collaboration with Queen’s University, Canada and the International Study Centre (ISC) at Herstmonceux Castle, will hold a three-day, interdisciplinary summer workshop on the topic of Music, Pattern and Mathematics.
The aim of the meeting is to bring together scientists, theorists, educators and performers to consider the abstract, physical, structural and numerical relationships between music and mathematics. The meeting will include presentations, discussions, workshops, and musical performances and will be held at the beautiful venue of Herstmonceux Castle, East Sussex.
For more details see
http://www.music.ed.ac.uk/Research/imhsd/MusicPatternMaths2010/index.html
June 16, 2010
Algebraic Model Structures
Posted by Tom Leinster
Guest post by Emily Riehl
Here’s a quick definition of a model structure on a complete and cocomplete category : a model structure consists of three classes of morphisms - the cofibrations, fibrations, and weak equivalences - such that satisfies the 2-of-3 property and and are weak factorization systems.
A weak factorization system (henceforth wfs) consists of two classes of maps, closed under retracts, such that elements of the left class lift against elements of the right, as depicted below,
and such that every morphism can be factored as an arrow in followed by an arrow in .
In examples, we typically think of the right class as a collection of morphisms satisfying some property, but it is also possible to conceive of them algebraically, that is, to incorporate the defining lifting property into a piece of structure attached to each given morphism. In one familiar example, the unalgebraicized perspective defines a Hurewicz fibration to be a map of spaces with the homotopy lifting property, while the algebraicized perspective equips each such with the structure of a path lifting function. Using this idea, we define a new notion of algebraic model structure, introduced below, whose wfs are replaced with natural weak factorization systems. This algebraization is inobtrusive - it can be given in many familiar situations simply by making choices that are known to exist and does not affect the underlying model structure, except possibly by producing better factorizations - but has many interesting features because the algebraicized wfs satisfy better categorical properties.
June 13, 2010
This Week’s Finds in Mathematical Physics (Week 299)
Posted by John Baez
In week299 of This Week’s Finds, hear about the school on Quantum Information and Computer Science that was recently held in Oxford, and also the workshop on Quantum Physics and Logic. Watch videos of the talks! Learn how classical structures give Frobenius algebras, and how complementary classical structures almost give bialgebras:
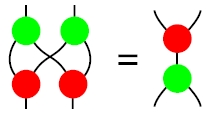
Admire the program called “Quantomatic”, which automatically carries out string diagram computations. Hear about Aaron Fenyes’ no-cloning theorem for classical mechanics. And finally, learn about “pre-Lie algebras” — algebraic gadgets with deep connections to trees, operads, and the work of Connes and Kreimer on renormalization in quantum field theory.
June 9, 2010
Boycotting the Nature Publishing Group
Posted by John Baez
The Nature Publishing Group publishes not only the prestigious journal Nature, but also many others. When this company bought Scientific American, it raised the institutional subscription price seven-fold. Now they are insisting on quadrupling the fees for 67 journals to which the University of California subscribes.
Right now, we pay them an average of $4,465 per year for each journal we subscribe to. After the increase, this would soar to $17,479 per year.
In response, the University of California is considering a system-wide boycott of the Nature Publishing Group — for example, cancelling subscriptions to all their journals.
June 8, 2010
At “Geometry, Quantum Fields, and Strings: Categorial Aspects”
Posted by Urs Schreiber
This week at Oberwolfach takes place a workshop titled Geometry, Quantum Fields, and Strings: Categorial Aspects, organized by Peter Bouwknegt, Dan Freed, Christoph Schweigert.
The workshop’s webpage is here.
Vladimir Arnold, 12 June 1937 - 3 June 2010
Posted by David Corfield
Perhaps people have memories they’d like to share of Vladimir Arnold who died last week.
Arnold had very strong views on education, which he was not reluctant to impart, as in this Interview in the Notices of the AMS (April 1997), and in The antiscientifical revolution and mathematics:
In the middle of the twentieth century a strong mafia of left-brained mathematicians succeeded in eliminating all geometry from the mathematical education (first in France and later in most other countries), replacing the study of all content in mathematics by the training in formal proofs and the manipulation of abstract notions. Of course, all the geometry, and, consequently, all relations with the real world and other sciences have been eliminated from the mathematics teaching.
The writings I’ve enjoyed most, though, are the Toronto Lectures and Polymathematics: is mathematics a single science or a set of arts? found on this page of lectures.

Image: www.kremlin.ru
June 7, 2010
Tensor Categories in Fredericton
Posted by Mike Shulman
While other people are having fun at QPL in Oxford, a bunch of us have been having our own fun on the other side of the pond, at a special session on “Tensor categories” at the summer meeting of the Canadian Mathematical Society in Fredericton, New Brunswick. I thought I’d share a few of the highlights that might be of most interest to you all.
June 2, 2010
Categories, Logic and Physics 7 at Birmingham
Posted by John Baez
Category theory, logic and the foundations of physics are taking an exciting new turn, prompted in part by work on quantum information theory. So if you feel sad that you missed all the fun at the Quantum Physics and Logic conference in Oxford last weekend, don’t just sit there moping! There’s still hope! You can go to Birmingham in September!
- 7th Workshop on Categories, Logic and Physics, Tuesday September 21st, 2010, University of Birmingham, School of Computer Science. Local organizers: Steve Vickers and Bertfried Fauser. Workshop coordinators: Bob Coecke and Andreas Doering.
 Posts with this logo use
Posts with this logo use 














