August 30, 2009
This Week’s Finds in Mathematical Physics (Week 278)
Posted by John Baez
In week278 of This Week’s Finds, hear how astronomers in a high desert in Chile use an "artifical star" to take photos of incredibly high resolution, and how this helped them spot what’s happening on Betelgeuse. Read how red supergiants like Betelgeuse and Ras Algethi spew out huge amounts of dust, which eventually forms planets like ours. Watch a Moon-sized object crash into a Mercury-sized one in a "hypervelocity collision" in a distant solar system:

Learn the new way to make graphene, and read my history of the Earth - for physicists. And when you’re ready: dive into groupoidification!
August 27, 2009
Feynman the Babylonian
Posted by David Corfield
When I next get around to teaching philosophy of science again I think I’ll have my students watch an episode or two from Feynman’s Messenger series of lectures. With the possibility of having studied only humanities subjects from the age of 16 it’s no surprise that there’s many a student with only the sketchiest idea of physics. Last time around when I asked the class to name any of Newton’s laws of motion, a long wait ensued before someone finally proffered an approximation to the first.
I was watching the second lecture yesterday, towards the end of which Feynman distinguishes between what he calls a ‘Babylonian’ approach and a ‘Greek’ one. His idea here is that mathematicians have a tendency to arrange their theories in the Greek style on an axiomatic basis, while this can’t work in physics, at least in a time of theoretical growth, because it is never clear which approach is basic. For example, one may view a physical theory in terms of forces or field potentials or conservation laws or paths of least action, and unpredictably any one of them might provide new insight as to how to link together physical facts.
August 23, 2009
Higher-Dimensional Algebra VII: Groupoidification
Posted by John Baez
Check this out:
- John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII: groupoidification — latest version with all known corrections, arXiv version or published version.
This is a somewhat expanded and improved version of our paper Groupoidification made easy, more suitable for publication. It now includes material on Hall algebras — or, very loosely speaking, quantum groups — and various different recipes for turning spans of groupoids into linear operators between vector spaces.
Comments and corrections are most welcome!
August 21, 2009
Notes on Differential Nonabelian Cohomology
Posted by Urs Schreiber
I have begun to prepare on my personal Lab page notes on stuff that I am working on. Some of it is in a state that should be readable and on which I would enjoy getting comments. This I want to present here.
The entry point for the technical material is here:
- Lab/schreiber/differential nonabelian cohomology
Behind the above link you find pointers to more information.
So far the material available there concerns the abstract definition of differential cohomology in an arbitrary -topos and the derivation from that of the notion of -Cartan-Ehresmann connection on principal -bundles.
August 19, 2009
nLab Migration
Posted by Urs Schreiber
As you may have heard, we had various reasons to migrate the Lab wiki to a different server. Thanks to tremendous help from Andrew Stacey this is now essentially achieved.
We have a trial version of the migrated Lab up and running now, here:
Before we officially migrate, change DNS servers and redirect everything to the new server, we’d like to ask you to test the new installation by messing around with it.
Please, if you have a minute, go to the migrated installation and look around the entries, try editing some entries etc, as if the whole thing were a huge sandbox.
The point is to have a look around and see if anything looks or feels different to the original. Please notify us about anything weird that you spot, anything that might have been broken in the migration process.
Notify us by dropping a comment at the Forum.
Beware. We have not yet officially migrated. Any changes made at the new migrated installation will be lost when we do the proper migration. This is just a test run.
For the time being, all actual content that you want to contribute is still to be edited at the Lab at its original URL. In fact, in the end we will redirect URLs accordingly, so that you will never submit any genuine contribution elsewhere than at http://ncatlab.org/nlab.
Thanks for your help.
August 17, 2009
Chasing around the Triangle
Posted by David Corfield
While looking about for material for a new Lab entry on foundations and philosophy, I came across Steve Awodey’s From Sets to Types to Categories to Sets. As the title of the paper suggests, Awodey chases around a triangle of foundational styles. In the process he demonstrates their equivalence.
August 15, 2009
The Pi Calculus
Posted by John Baez
After years of suffering, I finally feel I understand the lambda calculus — a programming language so simple that it’s ideal for theoretical computer science, with beautiful connections to category theory. Now I’m ready to move on down the Greek alphabet, and ask:
What’s the pi calculus?
It’s a famous example of a process calculus. Process begins with ‘p’. That explains the ‘pi’.
But what’s a ‘process calculus’?
August 13, 2009
Asymptotics of the Magnitude of Metric Spaces
Posted by John Baez
guest post by Tom Leinster
Simon Willerton and I have just arXived a new paper, On the asymptotic magnitude of subsets of Euclidean space. It’s about a subject that owes a lot to the -Café: the cardinality of metric spaces. Before we submit it to a journal, we’d be interested and grateful to have your comments — anything from typos to matters of philosophy.
Here’s the idea. Cardinality is supposed to play the same kind of role for metric spaces as ordinary cardinality plays for sets. Now, a fundamental property of the cardinality of finite sets is the inclusion-exclusion principle:
Here and are sets and means ordinary cardinality. But what if, say, and are compact subsets of and means metric cardinality? Does the inclusion-exclusion principle hold?
The answer is ‘no’, but it’s a particularly interesting ‘no’ — probably more interesting than ‘yes’ would have been. It’s ‘no, but asymptotically yes’, at least in the cases we’ve succeeded in analyzing.
Dan Ghica on Software vs Hardware
Posted by John Baez
Here’s a quick note from LICS ‘09. I’m too ignorant to offer a well-balanced summary of the conference, even apart from the fact that I missed the first day! So I won’t even try.
But here’s something I learned.
August 12, 2009
This Week’s Finds in Mathematical Physics (Week 277)
Posted by John Baez
In week277 of This Week’s Finds, find out what’s a million times thinner than paper, stronger than diamond, a better conductor than copper, and absorbs exactly
π α
of the light you shine through it.
August 10, 2009
Question about ∞-Colimits
Posted by Urs Schreiber
Here is a question on a certain peculiar configuration of -colomits also kown as homotopy colimits, where one hocolimits is taken over another hocolimit:
Suppose is an -groupoid and an -category and is an -functor of which we would like to compute some push-forward, such as, for simplicity, its -colimit
But let there be the following extra piece of datum: say the -groupoid itself comes to us exhibited as a homotopy colimit in -Grpd of a simplicial -groupoid which I’ll denote for reasons to be explained below: so suppose that we have a hocolimit expression
This is a peculiar higher categorical situation which does not have a 1-categorical analog: we have a hocolimit over a functor out of a domain that is itself a hocolimit:
Question: Are there any general useful facts one can know about such “hocolimits over hocolimits”?
In particular, let be the cocone components of induced by the universality property of the colimit. Is there an expression of the hocolim over in terms of that over its components?
By looking at the relevant diagrams, one is inclined to expect that – to some maybe imperfect extent – there might be a certain commutativity rule of the sort
where now the inner holcolim is over the component functors of , and the outer hocolim is over a resulting diagram in .
Here the trouble starts with saying precisely what that diagram in formed by the actually is. Below is considered as one special case the case where all are constant on a single object, in which case there is a simple answer.
To see why one might expect some such “hierarchical commutativity” rule for hocolimits or similar, maybe it is helpful to contemplate the relevant diagram in low degree of , where it looks like
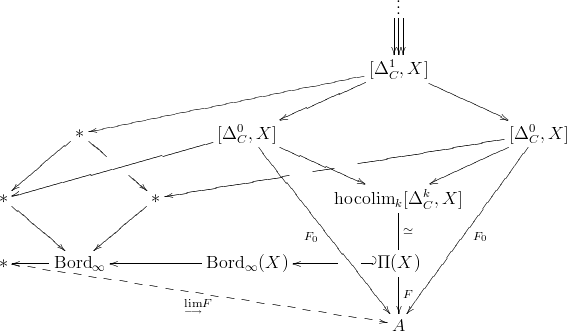
Here on the right is indicated the functor and the way it factors into components maps as a morphism out of a hocolimit.
Then to the left is indicated how itself as well as its components maps may be pushed forward to the point, meaning that their hocolimit, denoted there, are computed.
It seems from this that the colimiting cocones over the component functors want to assemble themselves to yield some kind of cocone over , much as the components themselves assemble to yield . But so far I keep getting a headache when trying to extract a precise statement along these lines.
By the way: in the above the map from to the point is factored in the curious way as indicated due to the way this question arises in the discussion of Quantization by Kan extension. More background information on that motivational aspect in the following.
August 9, 2009
What Do Mathematicians Need to Know About Blogging?
Posted by John Baez
Steven Krantz asked me to write an opinion piece about math blogging in the Notices of the American Mathematical Society. I asked if I could talk about this column on my blog, and even have people comment on drafts of it before it comes out in the Notices. He said okay.
So, just to get the ball rolling, let me ask: what do you think mathematicians need to know about blogging?
August 8, 2009
Computation and the Periodic Table II
Posted by John Baez
On Tuesday my wife Lisa and I are flying back from Paris to Los Angeles, and then taking the long shuttle ride from the airport back home to Riverside. But on Wednesday we’re driving back into LA. And then on Thursday morning at 8:30, if I don’t oversleep, I’m giving a talk here:
- Logic in Computer Science (LICS 2009), UCLA, August 11-14, 2009, program chair Andrew Pitts.
It’s called Computation and the periodic table, and you can see the slides now. Comments and corrections are welcome!
August 3, 2009
Question on Synthetic Differential Forms
Posted by Urs Schreiber
I am thinking about cosimplicial objects in the category of generalized smooth algebras as models for the -quantities (see there for what I mean) dual to models for -stacks.
The archetypical example should be the cosimplicial generalized smooth algebra of differential forms on a smooth space
for a smooth space, let be the generalized smooth algebra of functions on the infinitesimal -simplices in . As varies these naturally form a cosimplicial object.
Now, it seems to me as if the standard definition of the cochain complex of differential forms in synthetic differential geometry is nothing but the image of this under the (dual) Dold-Kan correspondence: is the normalized (dual) Moore complex as recalled in this dual form and in the present context in section 4 of
Castiglioni-Cortiñas: Cosimplicial versus DG-rings: a version of the Dold-Kan correspondence.
Details of what I have in mind are at differential forms in synthetic differential geometry.
My question is: am I hallucinating? If not, has this been discussed elsewhere`?
August 2, 2009
Groupoidfest 09
Posted by John Baez
It’s coming up, sooner than you think!
- Groupoidfest 09, October 24–25, 2009, Department of Mathematics, University of Colorado, Boulder, Colorado, organized by Arlan Ramsay.
Talks will start on Saturday morning and end around noon on Sunday. There is still time available for more speakers. Contact Arlan Ramsay if you are interested in speaking or attending! He can send you hotel information.
 Posts with this logo use
Posts with this logo use 














