Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

March 26, 2025

The McGee Group

Posted by John Baez

This is a bit of a shaggy dog story, but I think it’s fun. There’s also a moral about the nature of mathematical research.

Once I was interested in the McGee graph, nicely animated here by Mamouka Jibladze:

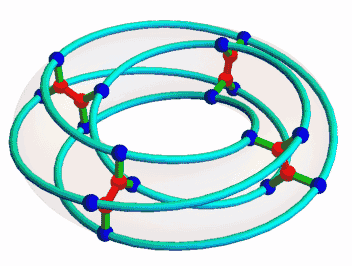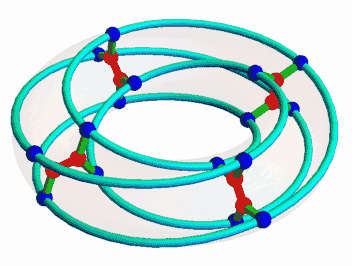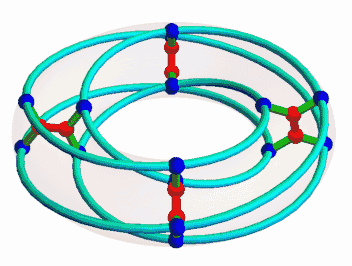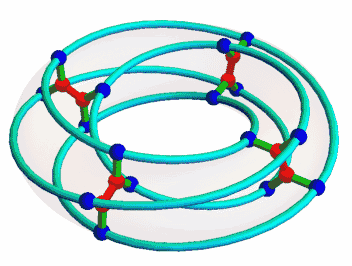
This is the unique (3,7)-cage, meaning a graph such that each vertex has 3 neighbors and the shortest cycle has length 7. Since it has a very symmetrical appearance, I hoped it would be connected to some interesting algebraic structures. But which?

Continue reading “The McGee Group” …
Posted at 6:33 PM UTC | Permalink | Followups (9)

March 20, 2025

Visual Insights (Part 2)

Posted by John Baez

From August 2013 to January 2017 I ran a blog called Visual Insight, which was a place to share striking images that help explain topics in mathematics.  Here’s the video of a talk I gave last week about some of those images:

It was fun showing people the great images created by Refurio Anachro, Greg Egan, Roice Nelson, Gerard Westendorp and many other folks. For more info on the images I talked about, read on….

Continue reading “Visual Insights (Part 2)” …
Posted at 3:59 AM UTC | Permalink | Post a Comment

March 12, 2025

Category Theory 2025

Posted by Tom Leinster

Guest post by John Bourke.

The next International Category Theory Conference CT2025 will take place at Masaryk University (Brno, Czech Republic) from Sunday, July 13 and will end on Saturday, July 19, 2025.

Brno is a beautiful city surrounded by nature with a long tradition in category theory. If you are interested in attending, please read on!

Important dates

  • April 2: talk submission
  • April 18: early registration deadline
  • May 7: notification of speakers
  • May 23: registration deadline
  • July 13-19: conference

In addition to 25 minute contributed talks, there will be speed talks replacing poster sessions, and we hope to accommodate as many talks as possible.

The invited speakers are:

  • Clark Barwick (University of Edinburgh)
  • Maria Manuel Clementino (University of Coimbra)
  • Simon Henry (University of Ottawa)
  • Jean-Simon Lemay (Macquarie University)
  • Wendy Lowen (University of Antwerp)
  • Maru Sarazola (University of Minnesota)
Continue reading “Category Theory 2025” …
Posted at 10:54 AM UTC | Permalink | Followups (2)

March 7, 2025

Visual Insights (Part 1)

Posted by John Baez

I’m giving a talk next Friday, March 14th, at 9 am Pacific Daylight time here in California. You’re all invited!

(Note that Daylight Savings Time starts March 9th, so do your calculations carefully if you do them before then.)

Title: Visual Insights

Abstract: For several years I ran a blog called Visual Insight, which was a place to share striking images that help explain topics in mathematics.  In this talk I’d like to show you some of those images and explain some of the mathematics they illustrate.

Zoom link: https://virginia.zoom.us/j/97786599157?pwd=jr0dvbolVZ6zrHZhjOSeE2aFvbl6Ix.1

Recording: This talk will be recorded, and eventually a video will appear here: https://www.youtube.com/@IllustratingMathSeminar

Continue reading “Visual Insights (Part 1)” …
Posted at 6:31 AM UTC | Permalink | Post a Comment

March 4, 2025

How Good are Permutation Represesentations?

Posted by John Baez

Any action of a finite group GG on a finite set XX gives a linear representation of GG on the vector space with basis XX. This is called a ‘permutation representation’. And this raises a natural question: how many representations of finite groups are permutation representations?

Most representations are not permutation representations, since every permutation representation has a vector fixed by all elements of GG, namely the vector that’s the sum of all elements of XX. In other words, every permutation representation has a 1-dimensional trivial rep sitting inside it.

But what if we could ‘subtract off’ this trivial representation?

There are different levels of subtlety with which we can do this. For example, we can decategorify, and let:

  • the Burnside ring of GG be the ring A(G)A(G) of formal differences of isomorphism classes of actions of GG on finite sets;

  • the representation ring of GG be the ring R(G)R(G) of formal differences of isomorphism classes of finite-dimensional representations of GG.

In either of these rings, we can subtract.

There’s an obvious map β:A(G)→R(G)\beta : A(G) \to R(G) , since any action of GG on a finite set gives a permutation representation of GG on the vector space with basis XX.

So I asked on MathOverflow: is β\beta typically surjective, or typically not surjective?

Continue reading “How Good are Permutation Represesentations?” …
Posted at 5:01 PM UTC | Permalink | Followups (9)