November 30, 2006
Puzzle #8
Posted by John Baez
Q: Which 39-year-old female mathematician was rumored in 1999 to be secretly in charge of one of the world’s largest countries?
Warning: since I first posted this puzzle, someone told me the rumor was not only false, but that it was an exaggeration to call this woman a “mathematician”. So: extra credit for more details on that issue!
November 29, 2006
Nicolai on E10 and Supergravity
Posted by Urs Schreiber
We have had several discussions here on how (parts of) the Lie algebra of the gauge group governing 11-dimensional # and 10-dimensional # supergravity can rightly be thought of in terms of semistrict Lie 3-algebras (equivalently: 3-term -algebras).
There are various reasons that make some people expect that these various supergravity theories describe certain facets of some essentially unknown single entity. The working title of this unknown structure is “M-theory”. You’ll see one proposal for a precise statement of this “M-theory hypothesis” in a moment.
In our discussions, I had made a remark on how the various Lie 3-algebras that play a role in supergravity might - or might not - be merged into a single structure here.
John rightly remarked that
This M-theory Lie 3-superalgebra should ultimately be something very beautiful and integrated, not a bunch of pieces tacked together, if M-theory is as Magnificent as it’s supposed to be.
There are various indications that the unifying governing structure behind much of the supergravity zoo are exceptional Kac-Moody algebras, in particular , , and maybe also .
In particular, if one takes 11-dimensional supergravity and compactifies it on a 10-dimensional torus, the resulting 1-dimensional field theory exhibits a gauge symmetry under the gauge group , where denotes something like the group manifold and something like the maximal compact subgroup of .
This, combined with the observation of certain symmetries appearing in the chaotic dynamics of (super)gravity theories near spacelike singularities, has lead a couple of people, most notably H. Nicolai, T. Damour, M. Henneaux, T. Fischbacher and A. Kleinschmidt, to suspect that the classical dynamics encoded in the equations of motion of 11-dimensional supergravity, including its higher order M-theoretic corrections, correspond to geodesic motion on the group manifold of the Kac-Moody group , or rather the coset .
Since is hyperbolic, it is, with current technology, impossible to conceive it in its entirety. Hence all this work is based on a technique, where one uses a certain level truncation of the Kac-Moody algebra to obtain tractable and useful approximations to the full object.
The idea is that expanding geodesic motion on in terms of levels this way, corresponds to expanding a supergravity theory in powers of spatial gradients of its fields close to a spacelike singularity.
For several years now, Hermann Nicolai and collaborators have slowly but steadily checked this hypothesis for low levels.
I had once reviewed some basic aspects of this here.
So far, to the degree of detail that has become accessible, the hypothesis has proven to be correct. And, as the M-theory hypothesis would suggest, not only can 11-dimensional supergravity be found, level by level (up to level 3, so far), in the geodesic motion on , but higher levels seem to correctly reproduce higher order corrections to supergravity which have been derived by other means. Moreover, depending on how one “slices” by means of its subalgebras, one finds that the same geodesic motion also reproduces the other maximal supergravity theories, like 10-dimensional type IIB supergravity and massive 10-dimensional IIA supergravity.
Up to recently, all this work was restricted to the bosonic degrees of freedom of these theories. One of the remarkable aspects of the theory was that it gave rise to the various bosonic fields that accompany the graviton field (the Riemannian metric) in supergravity theories, like the supergravity 3-form, and which ordinarily appear only after one requires supersymmetry.
Still, one would like to check the entire program also against the fermionic fields, like the gravitino. The obvious guess is that these appear on the -side as we pass from the geodesic motion of a spinless particle on to the motion of a spinning particle.
Results on this part of the project are now also appearing. Today has appeared a new preprint, where further progress in this direction is discussed:
Axel Kleinschmidt, Hermann Nicolai
K(E9) from K(E10)
hep-th/0611314.
Among other things, it is discussed how has certain finite-dimensional spinorial representations under which - on the corresponding supergravity side of things - the equation of motion of the gravitino is covariant.
Today Hermann Nicolai visited Hamburg and gave a talk on this stuff:
E. Nicolai
: Prospects and Challenges
(slides).
November 28, 2006
D-Branes from Tin Cans, II
Posted by Urs Schreiber
A brief note on how a 2-section of a transport 2-functor transgressed to the configuration space of the open 2-particle (string) encodes gerbe modules (Chan-Paton bundles) associated to the endpoints of the 2-particle.
November 27, 2006
NIPS 2006
Posted by David Corfield
In a week’s time I shall be in Vancouver attending the NIPS 2006 conference. NIPS stands for Neural Information Processing Systems. I’m looking forward to meeting some of the people whose work I’ve been reading over the past twenty months. Later in the week I shall be speaking up in Whistler at a workshop called ‘Learning when test and training inputs have different distributions’, and hopefully fitting in some skiing.
In a way you could say all of our use of experience to make predictions encounters the problem addressed by the workshop. If we include time as as one of the input variables, then our experience or ‘training sample’ has been gathered in the past, and we hope to apply it to situations in the future. Or from our experience gathered here, we expect certain things to happen there. How is it, though, that sometimes you know time, space, or some other variable, don’t matter, whereas other times you know they do?
November 25, 2006
Puzzle #7
Posted by John Baez
November 24, 2006
2-Monoid of Observables on String-G
Posted by Urs Schreiber
The baby version of the Freed-Hopkins-Teleman result, as explained by Simon Willerton, suggests that we should be thinking of the modular tensor category
that govers -Chern Simons theory and Wess-Zumino-Witten theory rather in terms of the representation category
of a central extension of the action groupoid
of the adjoint action of on itself.
This monoidal category should arise as the 2-monoid of observables # that acts on the 2-space of states over a point as we consider the 3-particle propagating on a target space that resembles .
In turn, this 2-monoid of observables should arise # as the endomorphisms of the trivial transport on target space
Here I would like to show that when we model target space as
where is the strict string 2-group #, coming from the crossed module # , then sections on configuration space of the boundary of the 3-particle form a module category for
As discussed elsewhere (currently at the end of these notes), this should imply that states over a point are a module for
November 23, 2006
The Baby Version of Freed-Hopkins-Teleman
Posted by Urs Schreiber
Recently I had discussed # one aspect of the paper
Simon Willerton
The twisted Drinfeld double of a finite group via gerbes and finite groupoids
math.QA/0503266 .
There are many nice insights in that work. One of them is a rather shockingly simple explanation of the nature of the celebrated Freed-Hopkins-Teleman result # - obtained by finding its analog for finite groups.
Here I will briefly say what Freed-Hopkins-Teleman have shown for Lie groups, and how Simon Willerton finds the analog of that for finite groups.
The 1-Dimensional 3-Vector Space
Posted by Urs Schreiber
I feel a certain need for 3-vector spaces, for 3-reps of 3-groups on 3-vector spaces. And things like that. But 1-dimensional 3-vector spaces would do.
Here I shall talk about how, for any braided abelian monoidal category , the 3-category
plays the role of the 3-category of canonical 1-dimensional 3-vector spaces.
Moreover, I would like to point out how morphisms between almost-trivial line-3-bundles with connection give rise to the 3-category of twisted bimodules that I talked about recently #.
This 3-category is a beautiful gadget. For and any commutative ring,
is discussed in the last part of
R. Gordon, A.J. Power and R. Street,
Coherence for tricategories,
Memoirs of the American Math. Society 117 (1995) Number 558.
John Baez describes this guy in TWF 209.
I first got interested in it here, but for a dumb reason it took me until last night to realize that this is the 3-category of canonical 1-dimensional 3-vector spaces that I was looking for all along.
For reading on, you have to leave the room and go to this file:
the 1-dimensional 3-vector space
A Third Model of the String Lie 2-Algebra
Posted by John Baez
One of the main themes of this blog is categorification: taking mathematical structures that are sets with extra structure, and replacing equations by isomorphisms to make them into categories. A wonderful fact is that any Lie algebra has a god-given one-parameter family of categorifications . We already have two ways to construct this gadget. Now this paper gives a third:
-
Friederich Wagemann, On Lie algebra crossed modules,
Communications in Algebra 34 (2006), 1699-1722.
Abstract: This article constructs a crossed module corresponding to the generator of the third cohomology group with trivial coefficients of a complex simple Lie algebra. This generator reads as , constructed from the Lie bracket and the Killing form . The construction is inspired by the corresponding construction for the Lie algebra of formal vector fields in one formal variable on , and its subalgebra , where the generator is usually called Godbillon-Vey class.
November 21, 2006
Classical vs Quantum Computation (Week 7)
Posted by John Baez
Here are this week’s notes on Classical versus Quantum Computation:
- Week 7 (Nov. 21) - The untyped lambda-calculus, continued. “Building a computer” inside the free cartesian closed category on an object with . Operations on booleans. The "if-then-else" construction. Addition and multiplication of Church numerals. Defining functions recursively: the astounding Fixed Point Theorem.
Last week’s notes are here; next week’s notes are here.
Basic Question on Homs in 2-Cat
Posted by Urs Schreiber
I have
John W. Gray
Formal Category Theory: Adjointness for 2-Categories
Springer, 1974
in front of me, but I haven’t absorbed it yet. I am looking for information about the following question:
In the world of strict 2-categories, strict 2-functors, pseudonatural transformations and modifications of these, consider three 2-categories
How is
related to
?
Here denotes the 2-category of 2-functors from to , pseudonatural transformations and modifications.
I am interested in this question, because it seems - unless I am hallucinating - to play a role in the construction of extended 2-dimensional quantum field theories #.
I see that one answer to this question is provided by item iii) of theorem I.4.14 of Gray’s text. But I need to better understand what this theorem tells me in practice.
Philosophy as Stance
Posted by David Corfield
Over at Ars Mathematica, John gave an explanation for the vituperative nature of the pro- vs anti- string theory discussions in the blogosphere:
The unpleasant nature of the whole extended argument can be seen as a collective cry of agony on the part of physicists trying and - so far - failing to find a theory that goes beyond the Standard Model and general relativity. Both string theorists and their opponents are secretly miserable over this failure.
To which I added:
I don’t have the book to hand, but the philosopher of science Bas van Fraassen has an interesting account of what happens as scientists become more desperate when nothing works. This is in ‘The Empirical Stance’, where he discusses Sartre’s Theory of the Emotions.
From the Internet Encyclopedia of Philosophy, we read:
In Sketch for a Theory of the Emotions, Sartre replaces the traditional picture of the passivity of our emotional nature with one of the subject’s active participation in her emotional experiences. Emotion originates in a degradation of consciousness faced with a certain situation. The spontaneous conscious grasp of the situation which characterizes an emotion, involves what Sartre describes as a ‘magical’ transformation of the situation. Faced with an object which poses an insurmountable problem, the subject attempts to view it differently, as though it were magically transformed. Thus an imminent extreme danger may cause me to faint so that the object of my fear is no longer in my conscious grasp. Or, in the case of wrath against an unmovable obstacle, I may hit it as though the world were such that this action could lead to its removal. The essence of an emotional state is thus not an immanent feature of the mental world, but rather a transformation of the subject’s perspective upon the world.
Without an unmovable obstacle to hit, there are always other people.
November 20, 2006
Derived Categories in Utah
Posted by Urs Schreiber
Eric Sharpe kindly informs me about the following event.
From June 4-16, 2007, there’ll be an intensive 2-week training session on derived categories:
Derived Categories School in Utah
for visiting grad students & postdocs in math & physics. It’ll be followed by a 1-week research workshop at the Snowbird resort.




If you want to get into the mood, try Eric Sharpe’s exposition Derived categories and D-branes.
This Week’s Finds in Mathematical Physics (Week 241)
Posted by John Baez
In week241 of This Week’s Finds, you can follow me on my tour of the Laser Interferometry Gravitational-Wave Observatory in Louisiana:

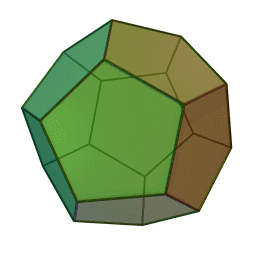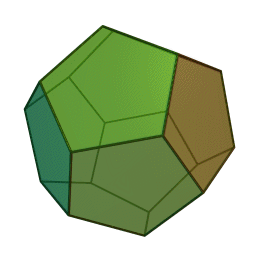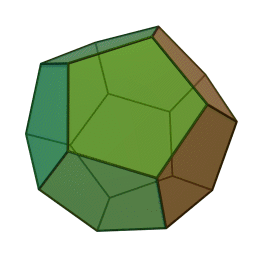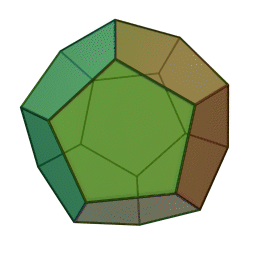
Also hear some tales of the dodecahedron… from the pyritohedron and Neolithic carved stone spheres, through the Pariocoto virus and dodecahedrane, all the way to its relation with the exceptional Lie group E8!
November 17, 2006
Categorical Trace and Sections of 2-Transport
Posted by Urs Schreiber
What is a trace?
In quantum field theory, the answer is: let be 1-functor describing an -dimensional QFT. Then the trace of
is
What is a 2-trace?
In an extended QFT we want to refine to an -functor #. Do we get an -trace this way?
Curiously, the right way to think of the extended is, apparently, to think in terms of spaces of sections of -bundles #.
I am trying to understand the implications of a general abstract proposal # for what that might actually mean.
As a consistency check, I would like to understand if in the case where the QFT’s target space is a 2-group and the 2-bundle is a 2-representation: does the canonical space of states
know about the notion of 2-character of a 2-representation as discussed by Kapranov and Ganter ?
November 16, 2006
MacIntyre on Rational Judgment
Posted by David Corfield
Let us continue to develop the MacIntyrean theme of belonging to a tradition of enquiry. The central practice with which MacIntyre has been concerned is the life of a moral-political community. But for any community to operate rationally, it must do so in terms of a common good, internal to the practice of that community, which in turn must engage itself in a quest to better understand this good which constitutes its end. Something I have worked on over previous months has been whether we can see the mathematical community in similar terms. So where your typical Anglo-American political philosopher or ethicist and their philosopher of mathematics colleague will have very little to talk about, this is not the case with MacIntyre and myself, hence the number of posts, both here and at the old blog, which I have devoted to him.
Now, what is it to perform well in a community?
Since what discriminates one kind of character from another is how goods are rank ordered by the agent, and since each rank ordering of goods embodies some conception of what the good life for human beings is, we will be unable to justify our choices until and unless we can justify some conception of the human good. And to do this we will have to resort to theory as the justification of practice.
Rationality however does not necessarily, nor even generally, require that we move to this point. I may on many types of occasion judge rightly and rationally that it is here and now desirable and choiceworthy that I do so and so, without having to enquire whether this type of action is genuinely desirable and choiceworthy for someone such as myself. I may on many types of occasion judge rightly and rationally that this type of action is desirable and choiceworthy for someone such as myself, without having to enquire whether the type of character that it exemplifies is genuinely good character. And I may judge rightly and rationally on many types of occasion that this type of character is indeed better than that, without having to enquire about the nature of the human good. Yet insofar as my judgment and action are right and rational they will be such as would have been endorsed by someone who had followed out this chain of enquiry to the end (in two senses of “end”). It is always as if the rational agent’s judgment and action were the conclusion of a chain of reasoning whose first premise was “Since the good and the best is such and such…” But it is only in retrospect that our actions can be understood in this way. Deduction can never take the place of the exercise of phronesis. (Ethics and Politics, CUP 2006: 36-37)
November 15, 2006
Classical vs Quantum Computation (Week 6)
Posted by John Baez
Here are last week’s notes on Classical versus Quantum Computation:
- Week 6 (Nov. 9) - Classical versus quantum lambda-calculus. From lambda-terms to string diagrams. Internalizing composition. The "untyped" lambda-calculus: building a computer inside the free cartesian closed category on an object such that . Church numerals and booleans.
The previous week’s notes are here; next week’s notes are here.
Quantization and Cohomology (Week 7)
Posted by John Baez
Here are yesterday’s notes on Quantization and Cohomology:
- Week 7 (Nov. 14) - From particles to strings and membranes. Generalizing everything we’ve done so far from particles () to strings () and membranes that trace out -dimensional surfaces in spacetime (). The concept of "-velocity". The canonical -form on the extended phase space , where is spacetime.
Last week’s notes are here; next week’s notes are here.
Higher Gauge Theory
Posted by John Baez
On Thursday I’m flying to Baton Rouge to give a talk on higher gauge theory and check out the nearby gravitational wave detector. You can see my slides here:
- John Baez, Higher gauge theory, Mathematics and Physics & Astronomy Departments, Louisiana State University, November 14, 2006.
If you’re an expert on this business, perhaps the only thing you may not have seen yet is a discussion of how theory in 4 dimensions is a higher gauge theory.
If you spot typos or other mistakes I would love to hear about them - especially before Thursday morning!
November 13, 2006
Breen on Gerbes and 2-Gerbes
Posted by John Baez
Back in the summer of 2004, at the Institute for Mathematics and its Applications, there was a workshop on -categories. It was an intense, exhausting affair. Amid endless talks on various definitions of weak -category, Larry Breen gave two talks introducing us to gerbes and 2-gerbes. As the conference proceedings slouch slowly towards completion, you can now read his presentation, which has been polished into an excellent paper:
-
Lawrence Breen, Notes on 1- and 2-gerbes, to appear in -Categories: Foundations and Applications, eds. J. Baez and P. May.
Abstract: These notes discuss in an informal manner the construction and some properties of 1- and 2-gerbes. They are mainly based on the author’s previous work in this area, which is reviewed here, and to some extent improved upon. The main emphasis is on the description of the explicit manner in which one associates an appropriately defined non-abelian cocycle to a given 1- or 2-gerbe with chosen local trivializations.
Quantization and Cohomology (Week 6)
Posted by John Baez
Here are the notes for last week’s class on Quantization and Cohomology:
-
Week 6 (Nov. 7) -
The canonical 1-form. The symplectic structure and the action of a loop in phase space. Extended phase space: the cotangent bundle of (configuration space) × time. The action as an integral of the canonical 1-form over a path in the extended phase space. Rovelli’s covariant formulation of classical mechanics, as a warmup for generalizing classical mechanics from particles to strings.
- Supplementary reading: Carlo Rovelli, Covariant hamiltonian formalism for field theory: Hamilton-Jacobi equation on the space G.
Quantization and Cohomology (Week 5)
Posted by John Baez
Still catching up… here are the notes for the Halloween class on Quantization and Cohomology:
-
Week 5 (Oct. 31) -
The canonical 1-form on . Symplectic structures. Why a symplectic structure should be a nondegenerate 2-form (so we get time evolution from a Hamiltonian) and closed (so time evolution preserves this 2-form). The action expressed in terms of the canonical 1-form.
- Homework: show that if is the canonical 1-form on the cotangent bundle of a manifold, then is a nondegenerate 2-form.
Puzzle #6
Posted by John Baez
November 12, 2006
Tales of the Dodecahedron
Posted by John Baez
I’m back from Dartmouth. On Friday I gave a math talk to a popular audience - full of pictures, history, jokes and magic tricks. Even you experts may enjoy the slides:
- John Baez, Tales of the dodecahedron: from Pythagoras through Plato to Poincaré, Reese Prosser Memorial Lecture, Dartmouth College, November 10, 2006.
November 10, 2006
The Tasks of Philosophy
Posted by David Corfield
- Murder is wrong.
- Copper conducts electricity.
- All even numbers greater than 2 are the sum of two primes.
- Liberal democracy is the best form of government.
- Nothing beyond the artwork is needed to appreciate it aesthetically.
November 9, 2006
Mathematics Under the Microscope
Posted by David Corfield
Alexandre Borovik has published the first chapter of his book, Mathematics Under the Microscope, at his website. It has been his experience as a blogger which persuaded him to opt for free access. I read the whole book a while ago and thoroughly recommend it. You even have the opportunity to send comments to the author.
Concerning a book for which there is not free access, in December you will at least be able to purchase my book more cheaply in paperback form for 25 pounds or 45 dollars.
November 8, 2006
Flat Sections and Twisted Groupoid Reps
Posted by Urs Schreiber
Tomorrow, Simon Willerton will be visiting Hamburg, giving a talk on Topological Field Theory and Gerbes. I have long meant to say something about one of his last papers on this subject, namely
Simon Willerton
The twisted Drinfeld double of a finite group via gerbes and finite groupoids
math.QA/0503266
While this paper is motivated by the desire to understand a certain groupoid algebra, the “Drinfeld double”, it actually does so by embedding the problem into a much larger context, namely the categorical description of topological field theory, and in particular of Dijkgraaf-Witten theory.
After sketching a general picture of topological field theory, which is a finite analog (finite in the sense of finite groups instead of Lie groups and finite groupoids instead of topological spaces) of the big picture that Michael Hopkins sketched for Chern-Simons theory, the paper demonstrates a couple of interesting cross-relations between apparently different topics that are obtained this way.
In particular, and that shall be the aspect which I will concentrate on here, Simon Willerton makes the point that one should think of representations of a finite groupoid which are twisted by a groupoid 2-cocycle, as flat sections of a gerbe with flat connection on that groupoid.
Below, I will briefly review some relevant aspects from the paper. Then I would like to propose a way to understand these spaces of sections in an arrow-theoretic manner, along the general lines that I talked about recently # in the context of categorified quantum mechanics.
My observation is that
the space of flat sections “over the -point” of an -bundle (-gerbe) with connection on a space is the space of natural transformations
where is the -particle and the transport functor # of the -bundle, as described here.
I claim that for the special cases of flat - and -bundles with connection this reproduces the twisted groupoid representations discussed by Simon Willerton in section 2.2 and 2.3 of the above paper.
Quantization and Cohomology (Week 4)
Posted by John Baez
Here are the notes for the October 24th class on Quantization and Cohomology:
-
Week 4 (Oct. 24) -
Hamiltonian dynamics and symplectic geometry. Hamiltonian vector fields. Getting Hamiltonian vector fields from a symplectic structure. The canonical 1-form on a cotangent bundle, and how this gives a symplectic structure.
- Homework: show the symplectic structure on the cotangent bundle gives , where the Hamiltonian vector field is given by
Quantization and Cohomology (Week 3)
Posted by John Baez
Sorry for the long pause! Here are the notes for the October 17th class on Quantization and Cohomology:
- Week 3 (Oct. 17) - From Lagrangian to Hamiltonian dynamics. Momentum as a cotangent vector. The Legendre transform. The Hamiltonian. Hamilton’s equations.
Last week’s notes are here; next week’s notes are here.
November 7, 2006
Chern-Simons Lie-3-Algebra Inside Derivations of String Lie-2-Algebra
Posted by Urs Schreiber
The -Category Café started with a discussion of the Lie 3-group underlying 11-dimensional supergravity #. In a followup #, I discussed a semistrict Lie 3-algebra with the property that 3-connections taking values in it are Chern-Simons 3-forms with values in , giving the local gauge structure of heterotic string backgrounds.
At that time I guessed that is in fact equivalent to the Lie-3-algebra of inner derivations of the Lie-2-algebra, using the fact that there is only a 1-parameter family of possible Lie 3-algebra structures on the underlying 3-vector space.
It would be quite nice if this were indeed true.
While I still have no full proof that is equivalent (tri-equivalent, if you like) to , I have now checked at least one half of this statement:
there is a morphism and one going the other way such that the composition is the identity on :
So at least sits inside :
The details can be found here:
Chern-Simons and Lie-3-algebras
This (rather unpleasant) computation is a generalization of that in the last section of From Loop Groups to 2-Groups, which shows the equivalence .
I take this as further indication # that the structure 3-group of -Chern-Simons theory is (a subgroup of) .
November 6, 2006
Dijkgraaf-Witten Theory and its Structure 3-Group
Posted by Urs Schreiber
Chern-Simons theory, for every choice of compact Lie group and class , is a theory of volume holonomies. Therefore one might want to understand it in terms of parallel 3-transport # with respect to a suitable structure 3-group.
A toy example for Chern-Simons theory is Dijkgraaf-Witten theory. This instead depends on a group 3-cocycle of a finite group .
As recently mentioned here, there are attempts to categorify Dijkgraaf-Witten theory by suitably replacing by some -group.
But do we even understand the ordinary theory in natural terms?
In particular, since Dijkgraaf-Witten theory, too, is a theory of parallel 3-transport, it should really come from a 3-group itself already. A 3-group, that is, which is naturally obtained from an ordinary finite group and a group 3-cocycle. And preferably in such a way that it illuminates the structure of Chern-Simons theory itself.
Which 3-group is that?
After briefly recalling the idea of Dijkgraaf-Witten theory, I shall argue that the 3-group in question is the inner automorphism 3-group
where is the skeletal weak 2-group whose group of objects is , whose group of morphisms is and whose associator is determined by the given group 3-cocycle .
This gives a concise way to say what Dijkgraaf-Witten theory is. It also fits in nicely with the claim # that the 3-group governs Chern-Simons theory - since # is essentially the Lie analog of .
Infinite-Dimensional Exponential Families
Posted by David Corfield
Back on my old blog I posted a few times on information geometry (1, 2, 3, 4). One key idea is the duality between projecting from a prior distribution onto the manifold of distributions, a specified set of whose moments match those of the empirical distribution, and projecting from the empirical distribution onto the corresponding exponential family. Legendre transforms govern this duality.
Now, one of the most important developments in machine learning over the past decade has been the use of kernel methods. For example, in the support vector machine (SVM) approach to classification, the data space is mapped into a feature space, a reproducing kernel Hilbert space. A linear classifier is then chosen in this feature space which does the best job at separating points with different labels. This classifier corresponds to a nonlinear decision boundary in the original space. The ‘Bayesian’ analogue employs Gaussian processes (GP).
November 5, 2006
Puzzle #5
Posted by John Baez
When was the Roman empire sold, and who bought it?
(Extra credit: how much did it cost?)
November 3, 2006
A 3-Category of Twisted Bimodules
Posted by Urs Schreiber
Those readers not yet bored to death by my posts might recall the following:
I was arguing that the 3-group controlling Chern-Simons theory (and maybe also the gauge structure of the Green-Schwarz mechanism #) is a sub-3-group of the inner automorphism 3-group #
of the String 2-group - for an ordinary Lie group (here assumed to be compact, simple and simply connected).
Part of the evidence (I, II) I presented was the observation that the canonical 2-representation # of on
apparently extends to a representation of on “twisted” bimodules, and that this representation seems to exhibit the expected structures #.
Like can be thought of as coming from lax functors into , for a 2-monoid (an abelian monoidal category), twisted bimodules
can be thought of as coming from lax functors into the endormorphism 3-monoid
of - in a way that is analogous to the step from the 2-group to its automorphism 3-group .
3-morphisms in look a little like the fundamental disk correlator with one bulk insertion in rational CFT #: a disk, bounded by bimodules, with a ribbon colored in running perpendicular through the disk’s center. (And this is not supposed to be a coincidence #.)
This picture suggests an obvious 3-category structure. That however is slightly oversimplified. On the other hand, the description in terms of lax functors into is a little too unwieldy.
Hence my goal here is to write down precisely and explicitly what looks like and how compositions are defined. Diagrams can be found in these notes:
a 3-category of twisted bimodules
The hard part is to check coherent weak properties, like the exchange law. I have checked what looked nontrivial - and am hoping that I haven’t overlooked anything. But if anyone has seen before anything like the 3-category that I am trying to describe here, please drop me a note.
November 2, 2006
Classical vs Quantum Computation (Week 5)
Posted by John Baez
Here are the notes for the latest installment of my course on Classical versus Quantum Computation:
- Week 5 (Nov. 2) - Theorem: evaluating the "name" of a morphism gives that morphism! The naturality of currying. A new "bubble" notation for currying and uncurrying. Popping bubbles to reveal the quantum world.
Last week’s notes are here; next week’s notes are here.
A Categorical Manifesto
Posted by John Baez
A while back Gina asked why computer scientists should be interested in categories. Maybe you categorical computer scientists out there have your own favorite answers to this? I’d be glad to hear them. To get you going, here’s one man’s answer:
-
Joseph Goguen, A categorical manifesto, Mathematical Structures in Computer Science 1 (1991), 49-67.
Abstract: This paper tries to explain why and how category theory is useful in computing science, by giving guidelines for applying seven basic categorical concepts: category, functor, natural transformation, limit, adjoint, colimit and comma category. Some examples, intuition, and references are given for each concept, but completeness is not attempted. Some additional categorical concepts and some suggestions for further research are also mentioned. The paper concludes with some philosophical discussion.
Academic Commons
Posted by David Corfield
David Bollier discusses the attempt by businesses to privatise the academic commons. Some universities eager to cash in are claiming the ‘knowledge assets’ created by staff and students as their own. Obstructive patenting is already hindering research into malaria vaccines. (This phenomenon is also termed tragedy of the anticommons.)
Perhaps mathematicians feel safer in their glorious isolation from worldly applications, only needing to fend off corporate profiteering by taking actions such as resigning en masse from the editorial boards of journals. (For other measures, see here.) But they’re getting closer. Bollier mentions that “It’s now possible to get patents on mathematical algorithms in software”. How long before the administration of your universe takes you to one side and tells you not to put your papers on the ArXiv, or write into this blog?
November 1, 2006
Klein 2-Geometry VII
Posted by David Corfield
Let’s reconvene the latest session of the Honorable Guild of Categorifiers of Kleinian Geometry. I’ll briefly sum up what I learned from last month’s efforts. Our plan had been to work out the projective 2-space associated to a Baez-Crans (BC) 2-vector space, find the 2-group of projective linear transformations, and then study sub-2-groups, in order to throw up 2-geometries which were categorifications of sub-geometries of projective geometry such as Euclidean or spherical geometry. But Urs posed for us the task of finding the general linear 2-group of such 2-vector spaces, and he helped it see the light of day, we think, here.
This suggested another path to Euclidean 2-geometry if we could find a way to put an inner product on a BC 2-vector space, and then look at the sub-2-group of transformations which preserve it. However, we met with a small problem. I wondered whether we might look to other forms of 2-vector space, -modules for categories other than Disc(), such as what we called (1,1) vector 2-spaces.
Elsewhere, David Roberts wondered whether we could use 2-ordinals to keep track of incidence relations between the objects of our 2-geometries.
Tim Silverman joined the team and wrote many comments, perhaps he would like to sum up his discoveries.
 Posts with this logo use
Posts with this logo use 














