Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

November 12, 2006

Tales of the Dodecahedron

Posted by John Baez

I’m back from Dartmouth. On Friday I gave a math talk to a popular audience - full of pictures, history, jokes and magic tricks. Even you experts may enjoy the slides:

Abstract: The dodecahedron is a beautiful shape made of 12 regular pentagons. It doesn’t occur in nature; it was invented by the Pythagoreans, and we first read of it in a text written by Plato. We shall see some of its many amazing properties: its relation to the Golden Ratio, its rotational symmetries - and best of all, how to use it to create a regular solid in 4 dimensions! Poincaré exploited this to invent a 3-dimensional space that disproved a conjecture he made. This led him to an improved version of his conjecture, which was recently proved by the reclusive Russian mathematician Grigori Perelman - who now stands to win a million dollars.

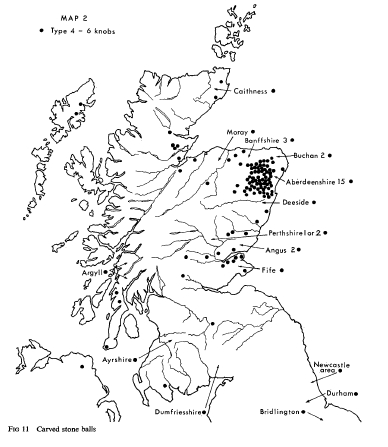
(By the way, when I say that the Pythagoreans invented the dodecahedron, I’m not claiming nobody else invented it first! According to Atiyah and Sutcliffe, these blocks found in Scotland date to around 2000 BC:

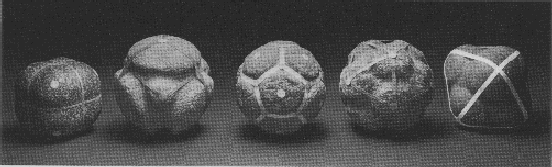
Should we count them as Platonic solids even if they’re rounded? That’s too tough a puzzle for me. Still less do I want to get into the question of whether the Platonic solids were invented or discovered!)

Posted at November 12, 2006 4:40 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1029



25 Comments & 0 Trackbacks

Re: Tales of the Dodecahedron

There’s a picture of Perelman linked at the Related Entry “Mathematics under the Microscope” that is rather apropos here.

Posted by: Allen Knutson on November 12, 2006 6:48 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

picture of Perelman

For those unfamiliar with the Russian alphabet, the word that looks like ‘HET!’ is actually ‘NYET!’, meaning ‘NO!’.

Posted by: Toby Bartels on November 14, 2006 7:30 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Dear John Baez,

After a little search, I found these:

A response post from Alison Roberts (Collections Manager, Department of Antiquities, Ashmolean Museum, University of Oxford).

An annotated bibliography, in particular:

Benno Artmann, “Symmetry Through the Ages: Highlights from the History of Regular Polyhedra”, in In Eves’ Circles, Joby Milo Anthony (ed.), Mathematical Association of America, pp. 139-148, 1994.

A short history. It includes references describing Platonic solids being carved in stone circa 2000 B.C.

Best wishes,
Christine

Posted by: Christine Dantas on November 12, 2006 11:34 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Thanks for the interesting references, Christine!

I wish they were all available online - Alison Roberts’ comments make me even more curious about those Scottish spheres.

Posted by: John Baez on November 12, 2006 5:04 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Your 10 NOV 2006 ‘Tales of …’ slides were great!

Answer to riddle of last slide:
“No hard decode” is an anagram for dodecahedron.

Posted by: Doug on November 12, 2006 2:37 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

I’m glad you like those slides! I was trying out a new method: using web pages, instead of making PDF files with LaTeX. For a talk with lots of pictures and movies, and not many equations, it seems to work well.

Posted by: John Baez on November 12, 2006 5:27 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

“Should we count them as Platonic solids even if they’re rounded?”

You should count them as Platonic solids if they have the same symmetry group as (the polygonal) Platonic solids, right?

Posted by: stephen on November 12, 2006 4:16 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

You should count them as Platonic solids if they have the same symmetry group as (the polygonal) Platonic solids, right?

Well, no - since then we’d have to count the cube and octahedron as the same, since they have the same symmetry group. The dodecahedron and icosahedron also have the same symmetry group.

So, there’s more to the essence of a regular polytope than its symmetry group. The question is: what?

In trying to answer this, modern mathematicians have decided that regular polytopes drawn on a sphere are more fundamental than those with planar faces. If we include these, the classification becomes more systematic! In addition to the usual Platonic solids, we get the hosohedra with nn bigons as faces, like this:

and their duals, the dihedra with two nn-gons as faces, like this:

(Both these pictures show the example where n=6n = 6.)

Including hosohedra and dihedra may seem weird at first, but it basically amounts to not discriminating against the number 2: we allow 2-sided polygons and allow 2 polygons to meet at an edge. This is naturally suggested by the Schläfli symbols for regular polytopes - those funny little symbols next to the pictures above, which are part of a very nice mathematical theory.

And, if we allow hosohedra and dihedra, the McKay correspondence works out much better!

So, it seems the early inhabitants of the British isles were in some ways further along than the Greeks in understanding the deep inner meaning of Platonic solids. I know McKay, and he likes this - national pride I guess.

However, I don’t know of any stone spheres that look like hosohedra or dihedra. The realization that 2 is a number just like 3, 4, 5,… came surprisingly late in the history of mathematics - perhaps because many languages, including early Celtic languages, have singular, plural and dual forms of nouns and pronouns.

I know your remark had a smiley under it, but I couldn’t resist taking it seriously, since it leads to some interesting issues.

Posted by: John Baez on November 12, 2006 4:53 PM | Permalink | Reply to this

A counterexample to the claim that…

…the regular dodecahedron doesn’t appear in Nature.

Posted by: Dan Piponi on November 12, 2006 10:09 PM | Permalink | Reply to this

Re: A counterexample to the claim that…

Okay, okay… so the regular dodecahedron has appeared in the journal Nature:

This is a Pariacoto virus with a dodecahedral cage of duplex RNA. Nice!

What I should have said is that people didn’t come up with the regular dodecahedron by seeing examples in nature. They might have seen the pyritohedron in crystals of fool’s gold, and “perfected” it.

Posted by: John Baez on November 12, 2006 11:22 PM | Permalink | Reply to this

Re: A counterexample to the claim that…

By the way, I think those models from Scotland are the most amazing thing I’ve seen in a long time. Is there any chance they’re a hoax? I’m astounded that someone in the culture of Scotland around 2000BC had the time, inclination and insight to make those models. This is the work of someone with a profound understanding of geometry. Could one person have come up with these from nothing, or was there a now lost intellectual culture so that these models are the result of the thought of many people over an extended period? Either way, it’s surprising for what was a neolithic culture. Given the popularity of stone circles in that part of the world, maybe there was a well developed culture of geometry. I wonder what other evidence of it exists.

Posted by: Dan Piponi on November 13, 2006 2:31 AM | Permalink | Reply to this

Those Scots had balls

Dan Piponi writes:

By the way, I think those models from Scotland are the most amazing thing I’ve seen in a long time.

Yeah, they’re cool.

Is there any chance they’re a hoax?

According to Alison Roberts, collection manager of the Ashmolean at Oxford, such carved balls have been found at late Neolithic and early Bronze Age sites throughout Scotland, with a few in North England and Ireland too. If they’re all hoaxes, that would have taken some work!

She says we should read this review article:

  • Dorothy N. Marshall, Carved stone balls, Proc. Soc. Antiq. Scotland, 108 (1976/77), 40-72.

Let’s see if we can get ahold of it.

Could one person have come up with these from nothing, or was there a now lost intellectual culture so that these models are the result of the thought of many people over an extended period?

If they’re all over Scotland, they’re probably the work of many people.

Either way, it’s surprising for what was a neolithic culture. Given the popularity of stone circles in that part of the world, maybe there was a well developed culture of geometry.

Maybe! For what it’s worth, stone balls of this sort date from the Late Neolithic to the Early Bronze Age: 2500 BC to 1500 BC.

By comparison, the megaliths at Stonehenge date back to 2500-2100 BC, with some bits going back to 3100 BC, and some nearby Mesolithic postholes all the way back to 8000 BC. Building Stonehenge took some serious social organization, and maybe some serious interest in geometry and astronomy too. I’ve read some cool theories about that, but they’re really controversial.

So, I guess we only see a trace here and there of what could have been some fairly sophisticated cultures. Too bad we can’t travel back in time and learn more…

Posted by: John Baez on November 13, 2006 3:38 AM | Permalink | Reply to this

Re: Those Scots had balls

“Let’s see if we can get ahold of it.”

If you do get hold of that paper, I’d love to read some comments on it.

Thinking about it, maybe it was only natural that the Scots moved up a dimension from stone circles to stone spheres. They just weren’t able to build them on quite the same scale.

Posted by: Dan Piponi on November 14, 2006 1:27 AM | Permalink | Reply to this

Re: Those Scots had balls

“Let’s see if we can get ahold of it.”

Wow. That was hard.

First, go here:

http://www.socantscot.org/ProceedingsSAIR.html

And click in the Archaeology Data Service link (accept the terms – I was asked the first time).

And then, the link to the Proceedings of the Society of Antiquaries of Scotland.

There! – 108 (1976-77)

Very interesting. There are spirals and other patterns as well.

Best wishes,
Christine

Posted by: Christine Dantas on November 14, 2006 2:12 PM | Permalink | Reply to this

Re: Those Scots had balls

There is also a direct link to the PDF file; I didn’t have to agree to any terms (which may be an error in their system).

Posted by: Toby Bartels on November 14, 2006 7:17 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

My friend Garett Leskowitz, physical chemist and former participant in the Quantum Gravity Seminar, sent me the following email, which I have embellished with links and pictures:

How fun!

“The dodecahedron is a beautiful shape made of 12 regular pentagons. It doesn’t occur in nature; it was invented by the Pythagoreans, and we first read of it in a text written by Plato.”

It doesn’t occur in Nature, but sometimes she can be coerced a little:

          

There are also other “Platonic hydrocarbons” with links on this Wikipedia page.

I’ve attached the early papers on the first synthesis of dodecahedrane, C20H20, which was apparently pursued for about 20 years before total success. If you look at the papers, keep in mind that it is common practice in organic chemistry to leave out bonds to hydrogen atoms in the pictures. A vertex from which three lines emanate is understood to mean a carbon atom bonded to a hydrogen atom that is not shown.

One of my favorite molecules is alpha-boron, B12. Natural elemental boron has more than one allotrope (chemically distinct forms of an element, like dioxygen, O2, and ozone, O3), one of which is B12. The boron atoms are arranged so that each sits at a vertex of a regular icosahedron. This was known for years before C60 was discovered, but it never got as much press.

Regards,
Garett

The “other Platonic hydrocarbons” Garett mentions above are cubane :

and the hypothetical tetrahedrane:

which is unstable in isolation, but stable as part of Tetra(trimethylsilyl)tetrahedrane, which looks quite cute:

(Most of the pictures above are in the public domain; the picture of dodecahedrane is available via a GNU Free Documentation License.)

Here are the papers Garett sent me:

  • Robert J. Ternansky, Douglas W. Balogh and Leo A. Paquette, Dodecahedrane, J. Am. Chem. Soc. 104 (1982), 4503-4504.
  • Leo A. Paquette, Dodecahedrane - the chemical transliteration of Plato’s universe (a review), Proc. Nat. Acad. Sci. USA 14 part 2 (1982), 4495-4500.

The chemical syntheses of dodecahedrane look very pretty. For example, here are some reactions from the second paper:

Experts on higher category theory will recognize that, if we ignore the methyl groups and other radicals, this is precisely the proof of the “dodecahedral identity” satisfied by the pentagonator in any monoidal 2-category. Here the proof itself has been categorified, with the steps of the proof corresponding to the arrows between diagrams. A truly amazing example of the unity of math and physics!

(Just kidding.)

Posted by: John Baez on November 14, 2006 1:42 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Experts on higher category theory will recognize that, if we ignore the methyl groups and other radicals, this is precisely the proof of the “dodecahedral identity” satisfied by the pentagonator in any monoidal 2-category.

(Just kidding.)

Of course, there is an identity satisfied by that pentagonator (and more generally by the pentagonator in any 3-category), but it only has 6 pentagons in it (as well as 3 quadrilaterals for the naturality of the associator). So it’s a (nonregular) ennahedron, which I suppose one calls simply ‘associahedron’.

I think that Aaron Lauda (and Eugenia Cheng) had a diagram of this online that you could print, cut out, and put together, but maybe it was a diagram of something else. In any case, I can’t find it now, but it’s on page 14 here.

Posted by: Toby Bartels on November 16, 2006 4:53 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Christine Dantas wrote:

Wow. That was hard.

Wow! That was quick! I was planning to order it from the UC Santa Cruz library… but you made it quite unnecessary. So, with Toby’s help, everyone can easily read this amazing paper:

  • Dorothy Marshall, Carved stone balls, Proceedings of the Society of Antiquaries of Scotland 108 (1976/77), 40-72.

I hadn’t expected Scottish antiquaries to have gone online… I imagined them being a bit dusty and old-fashioned.

Executive summary: 387 carved stone balls have been found in Scotland, dating from the Late Neolithic to Early Bronze Age, with a wide variety of interesting geometric patterns carved on them. You can see lots of pictures of them in this article. Here are two of the maps showing where various types of balls have been found:

Posted by: John Baez on November 15, 2006 8:07 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Wow!!! what a wonderful lecture!

Posted by: Gina on November 16, 2006 12:42 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

For those who enjoy the rotating dodecahedron
they might also enjoy rotating the associahedron:

http://math.univ-lyon1.fr/~chapoton/stasheff.html

Posted by: jim stasheff on December 2, 2006 1:31 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Doubt is cast on neolithic Scots as classifiers of platonic solids.

Posted by: David Corfield on April 2, 2009 3:27 PM | Permalink | Reply to this

007 vertices of a 6-simplex; Re: Tales of the Dodecahedron

Greater doubt is cast on neolithic Scots as classifiers of, and carvers in stone, of the 6 platonic hypersolids. And the alleged stone-aged small stellated dodecahedron is not a premature Kepler-Poinsot solid, but merely the spiky ball of a mace from a William Wallace statue intended for Mel Gibson’s beachhouse in Malibu. Scottish Nationalist Party stalwart Sir Sean Connery refused to speak to this reporter.

Posted by: Jonathan Vos Post on April 3, 2009 1:34 AM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Can someone in Oxford examine the scene of the
crime in the Ashmolean where they have statutory
obligations to their visitors?

Does their dodecahedron have 14 or 12 faces?
Alison Roberts tells us 14.

Can the museum be persuaded to show someone
the whole surface of their “dodecahedron” and
not be two-faced about it?

Posted by: John mac on April 18, 2009 9:48 PM | Permalink | Reply to this

Re: Tales of the Dodecahedron

Can someone in Oxford examine the scene of the
crime in the Ashmolean where they have statutory
obligations to their visitors?

Does their dodecahedron have 14 or 12 faces?
Alison Roberts tells us 14.

Can the museum be persuaded to show someone
the whole surface of their “dodecahedron” and
not be two-faced about it?

Posted by: John mac on April 18, 2009 9:49 PM | Permalink | Reply to this

I was a teenaged Polyhedron; Re: Tales of the Dodecahedron

Thursday 16 April 2009 I spent an hour at Abraham Lincoln High School in Los Angeles having 33 9th-12th graders build the Platonic solids with paper, scissors, and glue. They particularly liked the regular dodecahedron.

I’d have the students then come to the white board with their constructs and fill in a line each of a table on the number of vertices, edges, and faces. Did so also with my models of pentagonal pyramid and triangular prism. Then, Friday 17 April 2009, had those who hadn’t finished the Platonic solids build some Archimedean solids. I’ve just finished doing statistics on a 10-question survey, which 29 of the 33 students completed.

Previously, I’d done this at a different high school in Los Angeles. To control free variables, both had predominantly Latino students, and both built shapes and filled out surveys on Friday.

I have nice powerpoint graphics of the survey results from the 1st school. Will do so this weekend for this 2nd school. Will give my AP Statistics Class a chance to crunch the numbers more deeply to verify what appear to be significant differences between boys and girls in this project, and to explore the correlations with survey questions of aesthetics, the amount of fun they had, the changes in their feeliongs about Geometry, and their belief that such work increases intelligence. No students yet have self discovered Euler’s polyhedral formula. So I figure that to take a bigger sample, or more advanced students, or a longer sequence of days for this solid geometry unit.

Posted by: Jonathan Vos Post on April 19, 2009 12:29 AM | Permalink | Reply to this

Post a New Comment