February 21, 2014
Metric Spaces, Generalized Logic, and Closed Categories
Posted by Emily Riehl
Guest post by Tom Avery
Before getting started, I’d like to thank Emily for organizing the seminar, as well as all the other participants. It’s been a lot of fun so far! I’d also like to thank my supervisor Tom Leinster for some very helpful suggestions when writing this post.
In the fourth instalment of the Kan Extension Seminar we’re looking at Lawvere’s paper “Metric spaces, generalized logic, and closed categories”. This is the paper that introduced the surprising description of metric spaces as categories enriched over a certain monoidal category . A lot of people find this very striking when they first see it, and it helps to drive home the point that enriched categories are not just ordinary categories with some extra structure on the hom-sets; in fact the hom-sets don’t have to be sets at all!
Lawvere also intended the paper to serve as an accessible introduction to enriched category theory, so it begins fairly gently with some basic definitions. For the purposes of this post however, I’ll assume the reader has at least seen the definitions of symmetric monoidal closed categories, -categories, and -functors. If not, everything you need can be found on the nlab.
February 13, 2014
Relative Entropy
Posted by John Baez
You may recall how Tom Leinster, Tobias Fritz and I cooked up a neat category-theoretic characterization of entropy in a long conversation here on this blog. Now Tobias and I have a sequel giving a category-theoretic characterization of relative entropy. But since some people might be put off by the phrase ‘category-theoretic characterization’, it’s called:
I’ve written about this paper before, on my other blog:
- Relative Entropy (Part 1): how various structures important in probability theory arise naturally when you do linear algebra using only the nonnegative real numbers.
- Relative Entropy (Part 2): a category related to statistical inference, and how relative entropy defines a functor on this category.
- Relative Entropy (Part 3): statement of our main theorem, which characterizes relative entropy up to a constant multiple as the only functor with a few nice properties.
But now the paper is actually done! Let me give a compressed version of the whole story here… with sophisticated digressions buried in some parenthetical remarks that you’re free to skip if you want.
February 12, 2014
Call for Papers: Symposium on the Foundations of Mathematics
Posted by David Corfield
EDIT: New Submission Deadline: 15 April 2014, Notification of Acceptance: 30 April 2014
A friend, John Wigglesworth, has asked me to announce the following conference. Perhaps he’ll let us know if pluralist homotopy type theorists are welcome ;).
I wonder if any progress has been made on my MO ‘multiverse’ question.
February 11, 2014
The Deteriorating Relationship Between Academics and the NSA
Posted by Tom Leinster
Stefan Forcey just alerted me to a long and reflective piece (edit: now paywalled) in the Chronicle of Higher Education about the relationship between the NSA and American academics — mathematicians in particular.
Now many academics are trying to be heard from the outside, arguing that the NSA’s spying tactics are proving counterproductive and that university researchers have a duty to stop assisting them. […]
In the months since Edward J. Snowden fled the United States with tens of thousands of electronic documents describing NSA practices, mathematicians are realizing that they are in the same position as nuclear physicists in the middle of the last century, and business students in more recent times — suddenly needing to figure out the ethics behind what they do, said Edward Frenkel, a professor of mathematics at the University of California at Berkeley.
February 10, 2014
Network Theory Talks at Oxford
Posted by John Baez
One of my dreams these days is to get people to apply modern math to ecology and biology, to help us design technologies that work with nature instead of against it. I call this dream ‘green mathematics’. But this will take some time to reach, since living systems are subtle, and most mathematicians are more familiar with physics.
So, I’ve been warming up by studying the mathematics of chemistry, evolutionary game theory, electrical engineering, control theory and information theory. There are a lot of ideas in common to all these fields, but making them clear requires some category theory. I call this project ‘network theory’. I’m giving some talks about it at Oxford.
(This diagram is written in Systems Biology Graphical Notation.)
February 5, 2014
Galois Correspondences and Enriched Adjunctions
Posted by Simon Willerton
This is the fourth post in a series on categorical ideas related to formal concept analysis (the other posts are linked below). I want to bring together the ideas of the previous posts and tell you what relations and Galois correspdonences have to do with profunctors and nuclei. To do that I have to tell you what happens when you think of posets as categories enriched over the category of truth values.
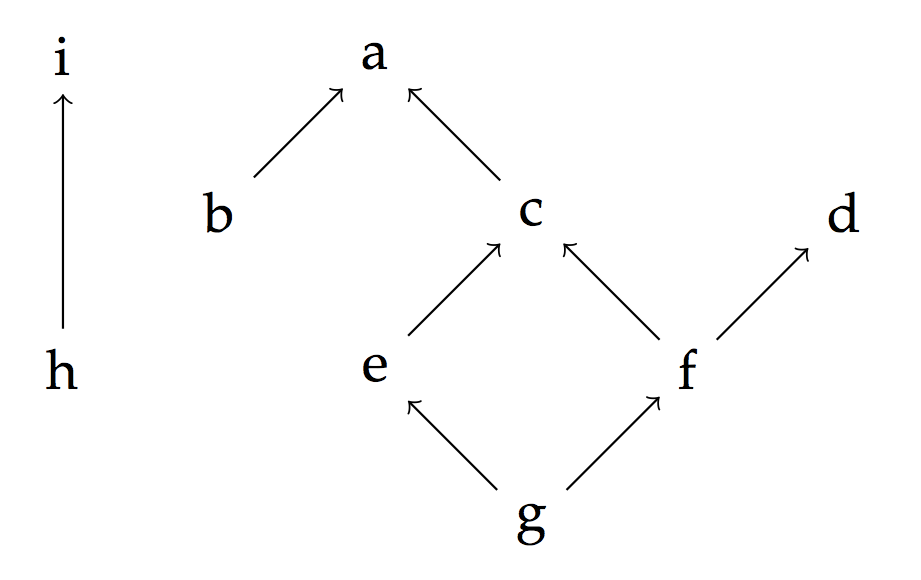
Here is a picture of a poset, with if you can climb up the arrows from to .
The picture can also be interpreted as representing a thin category, that is a category with at most one morphism between each pair of objects.
Most people who know what a category is know that a thin category is the same thing as a poset; with an arrow corresponding to the relation . However, despite being well-known, this fact is also not strictly true. You have to be wary of the antisymmetry axiom.
In a poset the antisymmetry axiom asserts that if and then , but this translates in a thin category to having morphisms and implying that and that is not true in general, all you can say is that is isomorphic to .
A poset-without-antisymmetry is called a preorder, and the true fact is that thin categories correspond to preorders (and posets correspond to skeletal, thin categories).
Less well-known than the above not-entirely-true fact, at least according to my unscientific straw poll of mathematicians, is that a category enriched over truth values is the same thing as a preorder. Although this seems, superficially, to be the same as the previous fact, it does have some deeper connotations due to the depths of enriched category theory. It is some of these depths that I want to start to explore here.
Categories of Continuous Functors
Posted by Emily Riehl
Guest post by Fosco Loregian
The aim of this note is to give a short account of
Freyd, P. J., & Kelly, G. M. (1972). Categories of continuous functors, I. JPAA, 2(3), 169-191.
as part of the Kan Extension Seminar series of lectures. I warmly thank all the participants and the organizer Emily Riehl for giving me this way of escape to the woeful solitude a “baby” category theorist (like I am preparing to become) suffers here in Italy. It is an amazing and overwhelming experience, I can’t even estimate the amount of things I already learned after these three lectures. There are two other people without whom this wouldn’t have been possible: my current advisor, D. Fiorenza, who patiently helped me to polish the exposition you are about to read, and my friend Paolo, for which the words “I don’t want to learn this” are meaningless.
That said, let’s begin with the real discussion.
Freyd and Kelly’s paper was the first to raise and solve in a very elegant way some fundamental questions in elementary Category Theory, the so-called Orthogonal subcategory problem, and Continuous functor problem.
February 2, 2014
An Emerging Pattern in Algebra and Topology II
Posted by Emily Riehl
Last time, I described an emerging pattern in algebra and topology, exemplified by the cohomology of the space of configurations of ordered points in the plane. In language I’ll introduce below, cohomology with rational coefficients defines a uniformly representation stable sequence, the fundamental data of which is an -representation for each .
In this post, I want to tell you in more detail about the representation stable sequences introduced in a paper by Tom Church and Benson Farb. I’ll also discuss the second generation approach to representation theory, which centers of the functor category of what they call FI-modules. Jordan Ellenberg, the third author of this paper, has blogged about this also. The first post in his series can be found here. In contrast with Part I, my exposition here will be more explicitly directed at the categorically-minded reader.
February 1, 2014
An Emerging Pattern in Algebra and Topology I
Posted by Emily Riehl
At the Joint Mathematics Meetings in Baltimore, I saw Benson Farb deliver a joint invited address on representation stability, the above eponymous “emerging pattern.” He began this work in 2010 with Tom Church, then a PhD student at the University of Chicago. I’ve been a fan for a few years now, and Benson’s beautiful talk has inspired me to write a brief summary.
This post is divided in two parts. In Part I, I’ll tell you about the talk, which was largely accessible to anyone with an undergraduate math background. In Part II, I’ll say a bit about the technical details and write about more recent developments, joint also with Jordan Ellenberg, in which some categorical ideas enable a simplified conceptual understanding of the patterns that frequently arise in practice.
 Posts with this logo use
Posts with this logo use