Galois Correspondences and Enriched Adjunctions
Posted by Simon Willerton
This is the fourth post in a series on categorical ideas related to formal concept analysis (the other posts are linked below). I want to bring together the ideas of the previous posts and tell you what relations and Galois correspdonences have to do with profunctors and nuclei. To do that I have to tell you what happens when you think of posets as categories enriched over the category of truth values.
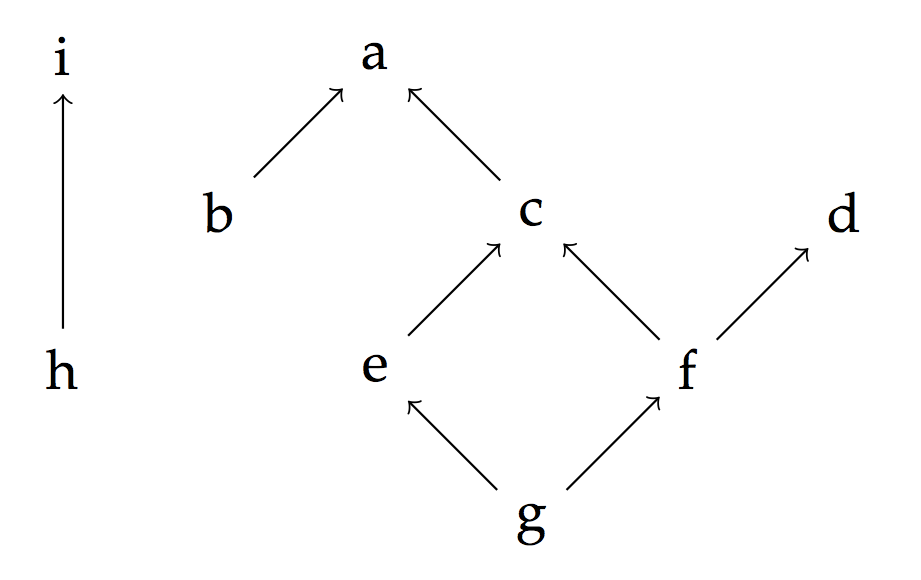
Here is a picture of a poset, with if you can climb up the arrows from to .
The picture can also be interpreted as representing a thin category, that is a category with at most one morphism between each pair of objects.
Most people who know what a category is know that a thin category is the same thing as a poset; with an arrow corresponding to the relation . However, despite being well-known, this fact is also not strictly true. You have to be wary of the antisymmetry axiom.
In a poset the antisymmetry axiom asserts that if and then , but this translates in a thin category to having morphisms and implying that and that is not true in general, all you can say is that is isomorphic to .
A poset-without-antisymmetry is called a preorder, and the true fact is that thin categories correspond to preorders (and posets correspond to skeletal, thin categories).
Less well-known than the above not-entirely-true fact, at least according to my unscientific straw poll of mathematicians, is that a category enriched over truth values is the same thing as a preorder. Although this seems, superficially, to be the same as the previous fact, it does have some deeper connotations due to the depths of enriched category theory. It is some of these depths that I want to start to explore here.
This follows on from three previous posts, but doesn’t require you to have read the other ones — unless you want to appreciate the punchline!
In The Nucleus of a Profunctor: Some Categorified Linear Algebra I gave a construction which starts with an enriched profunctor between two enriched categories and gives rise to an adjoint equivalence between certain presheaves and copresheaves on the two enriched categories. This is the nucleus construction.
In Formal Concept Analysis I gave a construction which starts with a relation between two sets and gives rise to a Galois correspondence between certain sets of subsets of the two sets.
In Classical Dualities and Formal Concept Analysis I gave examples of this construction popping up all over mathematics.
In this post I’ll try to convince you that the second construction is just an example of the first. I’ll do this by explaining what familiar (?!) concepts from ordinary category theory become when you work in categories enriched over truth values. This is summarized in the following dictionary.
In the rest of this post (which has got quite long) I will just explain how the translation arises. It is basic enriched category theory, so if you already understand the above dictionary you can stop reading now!
Next time I hope to explain when you apply the nucleus construction when you enrich over things more like the real numbers.
The enriching category
The category of truth values, , has two objects: and . The morphisms correspond to ‘logical entailment’ which is what working mathematicians would usually refer to as ‘implication’ but logicians reserve ‘implication’ for logical operation, we’ll see this below. Entailment is written (pronounced ‘entails’), so we have corresponds to the only non-identity morphism in . So the category can be simply pictured as follows. We can make this category of truth values into a monoidal category by using logical ‘and’ as the monoidal product; I’ll write this as .
Categories
A category enriched over , , consists of a set and for each we have the ‘hom-object’ . We should think of as being the truth of a relation . We need composition morphisms in this category, so for each triple, we need a morphism in truth values in this context it means we have an entailment or, in other words, if and then . So we have a transitive relation. We also need an identity for each , generally speaking this means we need a morphism (where is the monoidal unit) in this context it means or, in other words, . So the relation is also reflexive. Thus we have a preorder.
Conversely, a preorder gives rise to a category.
Slogan: -categories correspond to preorders.
Functors
There is a notion of an enriched functor which we can look at in this context. If we have two -categories and then a -functor consists of a function and, for each pair , a morphism in using square brackets to mean ‘the truth value of’ this is the same as or, in other words, preserves the order.
Slogan: -functors correspond to order preserving maps.
Natural transformation objects
Enriched category theory is richer if we enrich over a complete closed, symmetric monoidal category. If the category is complete then we means that we can make the collection of enriched functors between two enriched categories into an enriched category. If we have then we have a hom-object and this is given by an end In the context of enriching over , this end is just a big ‘and’, or a ‘for all’, if you prefer. Rewriting this is terms of truth values of the relations we get that this means In other words, given preorders and , there is a canonical preorder on the set of order preserving functions , and this is if and only if for all . We can say that is dominated by if .
Slogan: The -natural transformation object corresponds to the domination relation.
The closed structure
If the enriching category is closed then it can be considered as a category enriched over itself. There is a small problem here with type checking and we should be more precise. If is closed then there is an internal hom functor . We form a -category with the same objects as but with the hom-object given by the internal hom . People often use the same notation for and ; this is potentially confusing, but so you should do this with some care.
The category of truth values, , is closed and the internal hom is given by ‘logical implication’: . Here implication is understood in the logical operation sense and not the deductive sense (that’s what we are using entails for). So, using brackets purely for clarity,
Slogan: Internal hom for is implication.
We know that -categories are the same as preorders, so this gives a natural preorder on the set .
Slogan: The -category structure on corresponds to the preorder .
Presheaves and copresheaves
As we are considering a closed enriching category , we can think of as a -category and consider -functors into . This is like considering scalar valued functions on a vector space.
A presheaf on is a -functor and a copresheaf is a -functor . In the context of preorders and truth values, a presheaf is an order-reversing function and a copresheaf is an order-preserving function .
Knowing a function to is the same as knowing the preimage of , so we can identify a function with the subset . The order reversing condition translates into So is a downward closed subset of the preorder and all downward closed subsets arise in this way.
Similarly if is a copresheaf then it corresponds to an upward closed subset .
Because presheaves are -functors, we canonically have the domination relation between them. Given presheaves then which when translated to downward closed sets becomes
Slogan: The poset of presheaves on a preorder can be identified with the set of downward closed subsets equipped with the subset ordering.
Similarly, the domination relation on copresheaves corresponds to inclusion of the associated upward closed subsets. However, it is usually the opposite of the category of copresheaves that crops up, so this has the opposite relation.
Slogan: The poset of opcopresheaves on a preorder can be identified with the set of upward closed subsets equipped with the superset ordering.
Sets can be thought of as discrete posets, that is to say, where if and only if . In that case all subsets are both upward closed and downward closed. In this case, then, the set of copresheaves and the set of presheaves can both be identified with the powerset of the original set.
Slogan: The poset of presheaves on a set is the powerset with the subset ordering; the poset of opcopresheaves on a set is the powerset with the superset ordering
Adjunctions
An enriched adjunction consists of a pair of enriched functors together with an isomorphism in , natural in and This means that when we enrich over the category of truth values we get a Truth-adjunction being a pair of order-preserving maps between posets with the condition that In other words we have the following slogan.
Slogan: A Truth-adjunction is precisely a Galois connection between preorders.
Then the adjoint equivalence induced on the fixed sets is precisely the Galois correspondence induced on the fixed set of the Galois connection.
Profunctors
A profunctor between -categories and is an a -functor We should remind ourselves what the definition of the tensor product of -cateogries is. The set of objects of is the set of ordered pairs and the hom-sets are given by It is perhaps worth noting that in order to define composition we will need that has some extra structure such as being symmetric or braided.
When enriching over truth values, this means that for preorders and the preorder on is given by A profunctor in the case can then be identified with a subset of which is upward closed. Writing for , we have: This can make more sense if we expand it out: Slogan: Profunctors between preorders correspond to relations extending the preorders
Nuclei
In the first post in this sequence I showed that a profunctor gives rise to an adjunction between presheaves and opcopresheaves, and thus to an adjoint equivalence between the fixed sets of the adjunction.
In the third post I showed how a relation between sets gives rise to a Galois connection between the powersets and thus to a Galois correspondence between the sets of closed subsets. I also gave several examples of correspondences around different areas of maths that arise in this way.
I will leave it to the interested reader to show that the Galois correspondence construction is what you get when you apply the profunctor nucleus construction to the situation of discrete -categories. It should drop out from the dictionary.
Slogan: The nucleus of a profunctor between discrete categories corresponds to the Galois correspondence between the closed subsets coming from a relation between two sets.
That’s not a very snappy slogan to end with, I grant you.
Next time
In the next post I will show how costructing the nucleus of a profunctor when you enrich over something like the real numbers instead of truth values gives rise to some dualities in other areas of maths.

Re: Galois Correspondences and Enriched Adjunctions
Hi Simon. I just sent the following by email, which perhaps I shouldn’t have done as I’m on strike, and got back an autoreply saying that you wouldn’t be reading your email as you’re on strike. But perhaps you’ll read this…
Could you make the inserted graphic in your latest post a bit narrower? This is what happens on my browser. The graphic doesn’t appear until below the bottom of the right-hand menu bar, which means I have to scroll down five times in order to see it (and the rest of the Cafe front page). If the image was about 10% narrower, it would be fine, but who knows what happens with other people’s browsers. I guess it could be about 50% of its current width and still be legible.
Thanks!
Tom