September 21, 2014
A Packing Pessimization Problem
Posted by John Baez
In a pessimization problem, you try to minimize the maximum value of some function:
For example: which convex body in Euclidean space is the worst for packing? That is, which has the smallest maximum packing density?
(In case you’re wondering, we restrict attention to convex bodies because without this restriction the maximum packing density can be made as close to as we want.)
Of course the answer depends on the dimension. According to Martin Gardner, Stanislaw Ulam guessed that in 3 dimensions, the worst is the round ball. This is called Ulam’s packing conjecture.
In 3 dimensions, congruent balls can be packed with a density of
and Kepler’s conjecture, now a theorem, says that’s their maximum packing density. So, Ulam’s packing conjecture says we can pack congruent copies of any other convex body in with a density above .
Ulam’s packing conjecture is still open. We know that the ball is a local pessimum for ‘centrally symmetric’ convex bodies in 3 dimensions. But that’s just a small first step.
Geometry is often easier in 2 dimensions… but in some ways, the packing pessimization problem for convex bodies in 2 dimensions is even more mysterious than in 3.
September 10, 2014
Quasistrict Symmetric Monoidal 2-Categories via Wire Diagrams
Posted by Simon Willerton
Guest post by Bruce Bartlett
I recently put an article on the arXiv:
- Bruce Bartlett, Quasistrict symmetric monoidal 2-categories via wire diagrams.
It’s about Chris Schommer-Pries’s recent strictification result from his updated thesis, that every symmetric monoidal bicategory is equivalent to a quasistrict one. Since symmetric monoidal bicategories can be viewed as the syntax for ‘stable 3-dimensional algebra’, one aim of the paper is to write out this stuff out in a diagrammatic notation, like this:
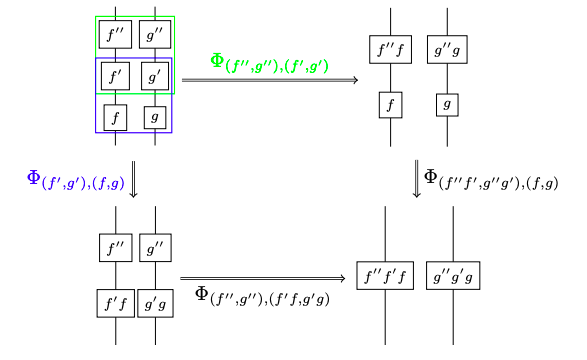
The other aim is to try to strip down the definition of a ‘quasistrict symmetric monoidal bicategory’, emphasizing the central role played by the interchangor isomorphisms. Let me explain a bit more.
September 6, 2014
Ronnie Brown in Paris
Posted by David Corfield
Ronnie Brown has brought to my attention a talk he gave recently at the Workshop Constructive Mathematics and Models of Type Theory, IHP Paris, 02 June 2014 - 06 June 2014.
Title: Intuitions for cubical methods in nonabelian algebraic topology
Abstract: The talk will start from the 1-dimensional Seifert-van Kampen Theorem for the fundamental group, then groupoid, and so to a use of strict double groupoids for higher versions. These allow for some precise nonabelian calculations of some homotopy types, obtained by a gluing process. Cubical methods are involved because of the ease of writing multiple compositions, leading to “algebraic inverses to subdivision”, relevant to higher dimensional local-to-global problems. Also the proofs involve some ideas of 2-dimensional formulae and rewriting. The use of strict multiple groupoids is essential to obtain precise descriptions as colimits and hence precise calculations. Another idea is to use both a “broad” and a “narrow” model of a particular kind of homotopy types, where the broad model is used for conjectures and proofs, while the narrow model is used for calculations and relation to classical methods. The algebraic proof of the equivalence of the two models then gives a powerful tool.
Slides are available from his preprint page.
 Posts with this logo use
Posts with this logo use 














