Quasistrict Symmetric Monoidal 2-Categories via Wire Diagrams
Posted by Simon Willerton
Guest post by Bruce Bartlett
I recently put an article on the arXiv:
- Bruce Bartlett, Quasistrict symmetric monoidal 2-categories via wire diagrams.
It’s about Chris Schommer-Pries’s recent strictification result from his updated thesis, that every symmetric monoidal bicategory is equivalent to a quasistrict one. Since symmetric monoidal bicategories can be viewed as the syntax for ‘stable 3-dimensional algebra’, one aim of the paper is to write out this stuff out in a diagrammatic notation, like this:
The other aim is to try to strip down the definition of a ‘quasistrict symmetric monoidal bicategory’, emphasizing the central role played by the interchangor isomorphisms. Let me explain a bit more.
Motivation
Firstly, some motivation. For a long time now I’ve been finishing up a project together with Chris Douglas, Chris Schommer-Pries and Jamie Vicary about 1-2-3 topological quantum field theories. The starting point is a generators-and-relations presentation of the oriented 3-dimensional bordism bicategory (objects are closed 1-manifolds, morphisms are two-dimensional bordisms, and 2-morphisms are diffeomorphism classes of three-dimensional bordisms between those). So, you present a symmetric monoidal bicategory from a bunch of generating objects, 1-morphisms, and 2-morphisms, and a bunch of relations between the 2-morphisms. These relations are written diagrammatically. For instance, the ‘pentagon relation’ looks like this:
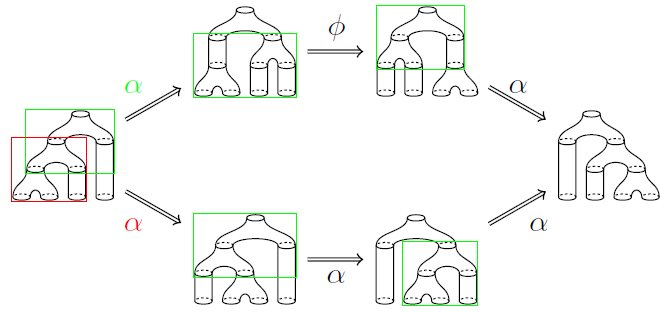
To make rigorous sense of these diagrams, we needed a theory of presenting symmetric monoidal bicategories via generators-and-relations in the above sense. So, Chris Schommer-Pries worked such a theory out, using computads, and proved the above strictification result. This implies that we could use the simple pictures above to perform calculations.
Strictifying symmetric monoidal bicategories
The full algebraic definition of a symmetric monoidal bicategory is quite intimidating, amounting to a large amount of data satisfying a host of diagrams. A self-contained definition can be found in this paper of Mike Stay. So, it’s of interest to see how much of this data can be strictified, at the cost of passing to an equivalent symmetric monoidal bicategory.
Before Schommer-Pries’s result, the best strictification result was that of Gurski and Osorno.
Theorem (GO). Every symmetric monoidal bicategory is equivalent to a semistrict symmetric monoidal 2-category.
Very roughly, a semistrict symmetric monoidal 2-category consists of a strict 2-category equipped with a strict tensor product, plus the following coherence data (see eg. HDA1 for a fuller account) satisfying a bunch of equations:
- tensor naturators, i.e. 2-isomorphisms
- braidings, i.e. 1-morphisms
- braiding naturators, i.e. 2-isomorphisms
- braiding bilinearators, i.e. 2-isomorphisms
- symmetrizors, i.e. 2-isomorphisms
So — Gurski and Osorno’s result represents a lot of progress. It says that the other coherence data in a symmetric monoidal bicategory (associators for the underlying bicategory, associators for the underlying monoidal bicategory, pentagonator, unitors, adjunction data, …) can be eliminated, or more precisely, strictified.
Schommer-Pries’s result goes further.
Theorem (S-P). Every semistrict monoidal bicategory is equivalent to a quasistrict symmetric monoidal 2-category.
A quasistrict symmetric monoidal 2-category is a semistrict symmetric monoidal 2-category where the braiding bilinearators and symmetrizors are equal to the identity. So - only the tensor naturators, braiding 1-morphisms, and braiding naturators remain!
The method of proof is to show that every symmetric monoidal bicategory admits a certain kind of presentation by generators-and-relations (a ‘quasistrict 3-computad’). And the gismo built out of a quasistrict 3-computad is a quasistrict symmetric monoidal 2-category! Q.E.D.
Stringent symmetric monoidal 2-categories
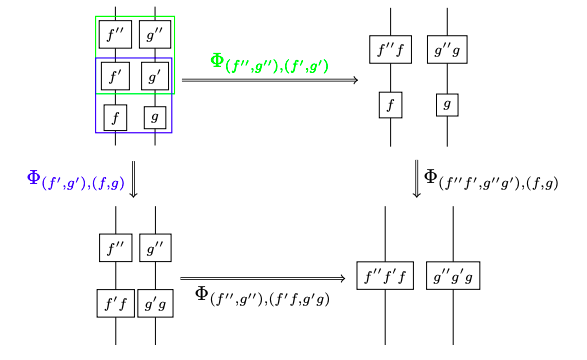
In my article, I reformulate the definition of a quasistrict symmetric monoidal 2-category a bit, removing redundant data. Firstly, the tensor naturators are fully determined by their underlying interchangors ,
This much is well-known. But also, the braiding naturators are fully determined by the interchangors. So, I define a stringent symmetric monoidal 2-category purely in terms of this coherence data: interchangors, and braiding 1-morphisms. I show that they’re equivalent to quasistrict symmetric monoidal bicategories.
Wire diagrams
The ‘stringent’ version of the definition is handy, because it admits a nice graphical calculus which I call ‘wire diagrams’. I needed a new name just to distinguish them from vanilla-flavoured string diagrams for 2-categories where the objects of the 2-category correspond to planar regions; now the objects of the 2-category correspond to lines. But it’s really just a rotated version of string diagrams in 3 dimensions. So, the basic setup is as follows:
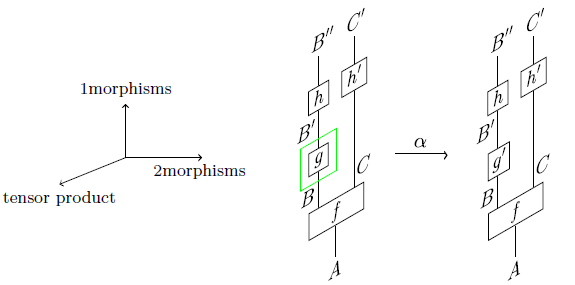
But to keep things nice and planar, we’ll draw this as follows:
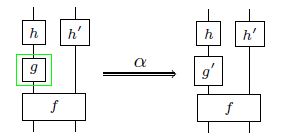
These diagrams are interpreted according to the prescription: tensor first, then compose! So, the interchangor isomorphisms look as follows:
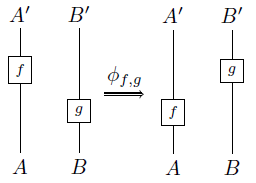
So, what I do is write out the definitions of quasistrict and stringent symmetric monoidal 2-categories in terms of wire diagrams, and use this graphical calculus to prove that they’re the same thing.
That’s good for us, because it turns out these ‘wire diagrams’ are precisely the diagrammatic notation we were using for the generators-and-relations presentation of the oriented 3-dimensional bordism bicategory. For instance, I hope you can see the interchangor being used in the ‘pentagon relation’ I drew near the top of this post. So, that diagrammatic notation has been justified.

Re: Quasistrict Symmetric Monoidal 2-Categories via Wire Diagrams
The pentagon relation looks like K_4, when the rooted binary trees describe interactions of RP^1’s. These end up being really helpful in studying twistor-string amplitudes.