April 28, 2020
Group Cohomology and Homotopy Fixed Points
Posted by John Baez
I now have a better understanding of crossed homomorphisms and why they show up so prominently in Gille and Szamuely’s Central Simple Algebras and Galois Cohomology. I told the tale of my enlightenment on Twitter. Basically I just read Qiaochu Yuan’s blog posts on this subject, and discovered that I’d been struggling to understand exactly the things he had figured out and written about:
But I didn’t say enough about what I learned, since Twitter is not so good for that. So let me do that now.
Model Categories as a Chu Construction
Posted by Mike Shulman
A couple years ago I blogged about the polycategory of multivariable adjunctions and how it embeds in the 2-Chu construction . After my talk at the ACT@UCR seminar this week, some folks were hanging out at the category theory zulip, and Reid Barton asked
The theory of model categories is self-dual. Is there some useful way to embed {model categories + Quillen adjunctions} in Chu(something) (similarly to how embeds in )? Where “something” would be some flavor of “half a model category structure”, e.g., a cofibration category?
At first I thought the answer was “no”, but now I think it is “yes”. I don’t know whether the construction is good for anything, but I found it amusing, so I thought I would share.
April 24, 2020
Crossed Homomorphisms
Posted by John Baez
While reading Gille and Szamuely’s Central Simple Algebras and Galois Cohomology I’m finding myself frustrated by my poor understanding of in group cohomology.
Roughly speaking, classifies group extensions of a group by an abelian group on which it acts. classifies 2-group extensions of by an abelian group on which it acts. And so on —this continues on up forever. I love this story: I call it the layer-cake philosophy of cohomology. But I never figured out how or fit into this story!
If you blindly follow the pattern, should classify ways of extending a group by a group on which it acts to get a 0-group. But what does that mean? Is there any way to make it make sense? There must be.
(I won’t even try to think about this way. Not today anyway.)
April 16, 2020
Ultracategories and 2-Monads
Posted by David Corfield
We began a discussion of Jacob Lurie’s Ultracategories over here, in particular whether they may be construed as algebras for some 2-monad. Perhaps this topic deserves a post to itself, rather than appearing tucked at the end of a long and fascinating discussion about condensed/pyknotic mathematics.
I have just discovered a 1995 PhD thesis by Francisco Marmolejo, advised by Robert Paré, that’s very relevant. Unfortunately the only online access is to a very poor photocopy, here. Anyway, Marmolejo characterises Makkai’s ultracategories there in a 2-monadic way. This would still leave Lurie’s somewhat differently defined ultracategories on the to-do list.
There’s then a follow-up question of characterising any such 2-monads using the codensity monad construction if possible. There’s some ongoing codensity conversation over here.
April 15, 2020
Online Seminar Lists
Posted by Tom Leinster
As you know, many online maths seminars are now running. You could fill your days with nothing but!
This short post is to note that there are now several websites where you can find very useful calendars of online seminars. Here are some of them:
This probably isn’t the first time that someone’s made a list of lists of online talks. Perhaps there are many such lists of lists. If so, you know what to do.
April 9, 2020
Western Hemisphere Colloquium on Geometry and Physics
Posted by John Baez
Another online talk series: the Western Hemisphere Colloquium on Geometry and Physics (WHCGP). This biweekly online colloquium features geometers and physicists presenting current research on a wide range of topics in the interface of the two fields. The talks are aimed at a broad audience. They will take place via Zoom on alternate Mondays at 3pm Eastern, noon Pacific, 4pm BRT. (There will be no lecture on May 25, Memorial Day in the USA.) Each session features a 60 minute talk, followed by 15 minutes for questions and discussion. You may join the meeting 15 minutes in advance. Questions and comments may be submitted to the moderator via the chat interface during the talk, or presented in person during the Q&A session. These colloquia will be recorded and will be available on the WHCGP website asap after the event.
The first two talks are:
April 13, Edward Witten (IAS), Volumes and random matrices.
April 27, Kevin Costello (PI), Topological strings, twistors, and skyrmions.
April 6, 2020
A Categorical View of Conditional Expectation
Posted by John Baez
I always like to see categories combined with probability theory and analysis. So I’m glad Prakash Panangaden did that in his talk at the ACT@UCR seminar. Afterwards we had discussions at the Category Theory Community Server, and you can see them here if you’re a member:
https://categorytheory.zulipchat.com/
You can see his slides here, or download a video here, or watch the video here.
Structured Cospans and Petri Nets
Posted by John Baez
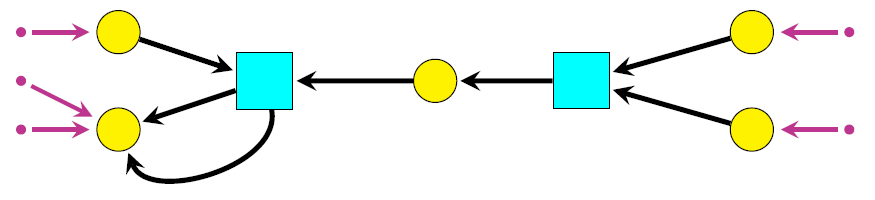
I’m giving a talk at the MIT Categories Seminar. It’ll be on Thursday April 9th, 12 noon Eastern Time.
You can see my talk live on YouTube here, with simultaneous discussion on the Category Theory Community Server. (To join this, click here; this link will expire in a while.) The talk will be recorded and remain available on YouTube.
You can already see the slides here.
Category Theory Calendar
Posted by John Baez
There are now enough online events in category theory that a calendar is needed. And here it is!
It should show the times in your time zone, at least if you don’t prevent it from getting that information.
 Posts with this logo use
Posts with this logo use 














