September 30, 2008
(ω+ω)-Categories (?)
Posted by Urs Schreiber
These days, everybody has his preferred definition of weak -categories. I have an idea, too, once mentioned somewhere here on the blog. It’s still very tentative. But when I looked yesterday at Todd Trimble’s operadic definition of weak -categories as discussed in
Eugenia Cheng
Comparing operadic theories of -categories
arXiv:0809.2070
I had the sensation that the definition I had in mind is not that unrelated, and maybe in fact a nice special case. Or maybe not, I haven’t really tried yet to go through this in detail. But nevertheless I feel like chatting about it.
Quantum Theory and Analysis
Posted by John Baez
Besides my seminar and an undergrad calculus couse, I’m also teaching a graduate math class on quantum mechanics. I won’t blog about this class, but you can see my lecture notes:
- John Baez, Quantum theory and analysis.
I wrote these notes the first time I taught the course, back in… 1989! I’d just been hired by UCR. I considered myself a mathematical physicist, but I was officially classified as an ‘analyst’ — since my specialty was nonlinear wave equations. Seems like a long time ago. But, I still like quantum theory and analysis.
Lie Theory Through Examples 1
Posted by John Baez
Simple Lie groups and Lie algebras tie together some of the most beautiful, symmetrical structures in mathematics: Platonic solids and their higher-dimensional cousins, finite groups generated by reflections, lattice packings of spheres, incidence geometries, symmetric spaces, and more. In this fall’s seminar we’ll explore this web of ideas through examples, starting with easy ‘classical’ ones and working up to ‘exceptional’ ones such as the 248-dimensional Lie group .
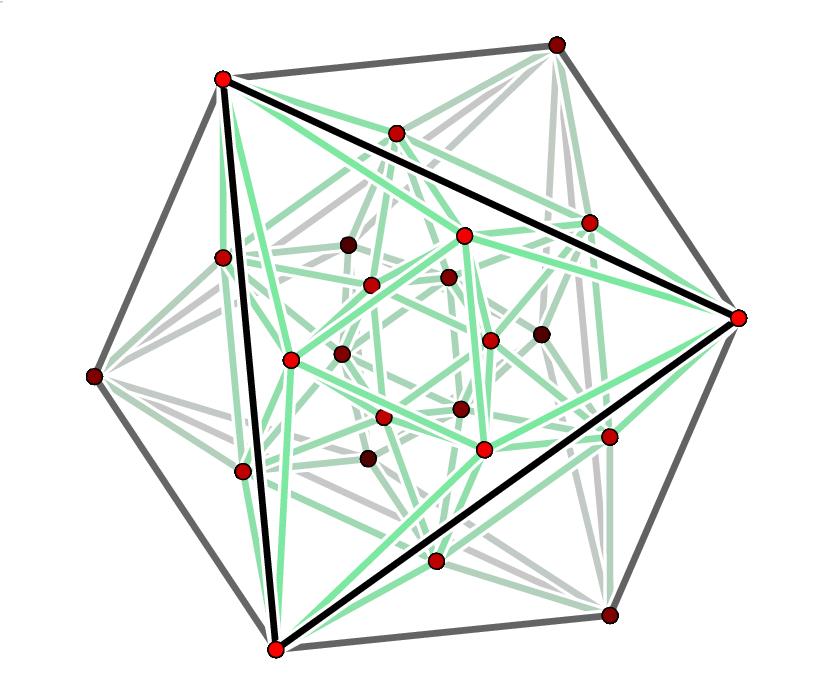
(Here are the 24 roots of , projected from 4 dimensions down to 3, and then drawn on the plane.)
September 27, 2008
OctoberFest 08
Posted by John Baez
- OctoberFest 08, Concordia University, Montreal, October 4–5, 2008.
Some Model ω-Questions
Posted by Urs Schreiber
Here are some questions related to generalizing the model structure on , the closed 1-category of strict -categories, as described in A folk model structure on , to the case of -categories internal to some presheaf topos.
September 26, 2008
Mathematical Miniatures
Posted by David Corfield
While looking about the web for something on Eckmann-Hilton duality, I stumbled across Beno Eckmann’s Mathematical Miniatures, a collection of 13 short essays I hadn’t noticed before.
September 22, 2008
Group Cocycles and Simplices
Posted by Urs Schreiber
Christoph Wockel asks me to forward the following question to the -Café:
What is a reference for a generalisation of the following canonical cocycle to higher dimensions?
Let be a connected (locally contractible) topological group and take a section continuous on a neighbourhood of the neutral element, of the endpoint evaluation map from the space of continuous paths starting at the neutral element of . Then the assignment is a -valued group 2-cocycle on , describing the universal cover of as a central extension. Moreover, this cocycle is universal for discrete groups.
A similar construction works in higher dimensions, yielding for each -connected group a valued group -cocycle. Moreover, this cocycle is universal for discrete groups. I’ve been searching for a reference for this, but did not succeed.
Thanks for any hints.
September 21, 2008
Back and Catching Up
Posted by Urs Schreiber
After my stay at ESI in Vienna # I spent a week hiking in the Alps with my family. Amazing how much one can miss in one week. Below a list of things I need to catch up with.
The next two weeks I’ll be in Zagreb, visiting Zoran Škoda and Igor Baković with whom we are working on a project on nonabelian differential cohomology (with David Roberts, Hisham Sati and Danny Stevenson). I am hoping to be able to say more about this in a while. Am planning to talk about something at least related at Higher Structures 2008 in November.
September 15, 2008
The Volume of a Differentiable Stack
Posted by David Corfield
The anticipated paper by Alan Weinstein has arrived:
We extend Baez and Dolan’s notion of the cardinality of a discrete groupoid (equal to the Euler characteristic of the corresponding discrete orbifold) to the setting of Lie groupoids. Since this quantity is an invariant under equivalence of groupoids, we call it the cardinality, or volume in the smooth case, of the associated stack rather than of the groupoid itself. In the smooth case, since there is no natural measure like the counting measure in the discrete case, we need extra data to define the volume. This data has the form of an invariant section of a natural line bundle over the stack. Sections of a square root of this line bundle constitute an “intrinsic Hilbert space” of the stack.
Do you get quantities in all dimensions in these stacks? E.g., are there line elements?
September 12, 2008
5
Posted by John Baez
I take off for Glasgow tomorrow, so it’s about time to finish preparing my talks…
This one is the most elementary of the lot, about the number 5 and its rascally properties. As usual, you can click on the title to see the slides.
24
Posted by John Baez
My final talk in Glasgow will be about the number 24.
This has long been my favorite number, since it shows up throughout math and physics in mysterious, shocking and even monstrous ways… which seem to fit together in a gargantuan conspiracy, as if pure mathematics itself were the work of an insane god — or at least one with a devilish sense of humor.
You can see the transparencies for this talk by clicking on the title below. If you see mistakes in it, please let me know!
September 11, 2008
Planar Algebras, TFTs with Defects
Posted by Urs Schreiber
I am in Vienna at the ESI attending a few days of the program Operator algebras and CFT.
This morning we had a nice talk by Dietmar Bisch on
Dietmar Bisch, Paramita Das, Shamindra Kumar Ghosh
The planar algebra of group-type subfactors
(arXiv)
I had not really looked into planar algebras before. The Wikipedia entry gives some information but leaves out the crucial pictures. Noah Snyder and his guest blogger Emily Peters on Secret Blogging Seminar have a useful series of posts on the topic – with the pictures.
The generic picture is this one:

which I have stolen from Noah Snyder’s web site.
This picture shows a representative of a generic morphism of the planar tangle operad, whose objects are unions of circles with marked points and whose morphisms are isotopy classes of such disks as above, with disks in the interior taken out and non-intersecting lines drawn in the remainder, which may end on any of the boundaries. In addition, one generally considers this colored in some index set, i.e have a color assigned to each face.
Composition in the operad is the obvious one obtained from gluing in disks into the holes of another disk, such that all the boundary labels match. A planar algebra is a representation of this planar tangle operad, i.e. an algebra for the operad.
If you’d ask me how I would summarize this in few words i’d say:
A planar algebra is a 2d genus-0 TFT with defect lines.
When I mentioned this description to people here who know about defect lines they certainly agreed. But it seems that this description is not something used in the literature at this point (or is it somewhere??).
But it might be useful…
September 10, 2008
New Structures for Physics II
Posted by John Baez
guest post by Bob Coecke
This is the continuation of John’s idea for having a public review here at the café of some chapters for the New Structures for Physics volume(s) which I am editing.
So far we’ve been discussing Baez and Stay part I, Baez and Stay part II on categories, topology, logic and computation, Abramsky and Tzevelekos’ tutorial lecture notes on categorical logic, and Coecke and Paquette’s categories for the practicing physicist who is not so interested in category theory.
Who are Various?
Posted by David Corfield
If you’re in the Manchester area on Saturday 4 October with not much to do, why not join me at MIMS Workshop on New Directions in Philosophy of Mathematics? I’m talking there, and will be discussing what I’ve been writing for a contribution to a book on Lautman.
While looking at what can be seen of Lawvere’s Categories of Space and of Quantity article mentioned here, I remembered that Saunders Mac Lane had written the preceding article in the book – The Protean Character of Mathematics. In view of the fact that one of the cases Lautman treats is Galoisian duality, I was delighted to find on turning back the page in Google books that on page 13 he writes
Janelidze, 1988 Categorical formulation of Galois Structure
Various, 1990 One adjunction handles Galois and much more
Unfortunately, pages 11-12 are missing, but if memory serves, these two entries are just the end of a list starting out with Galois.
By ‘Janelidze, 1988’, is Mac Lane referring to
Galois theory in categories: the new example of differential fields, Proc. Conf. Categorical Topology in Prague 1988, World Scientific 1989, 369-380?
And who are ‘Various, 1990’, what is their single adjunction, and what is ‘much more’?
September 9, 2008
Reliability
Posted by David Corfield
Melvyn B. Nathanson has an article on the ArXiv today – Desperately seeking mathematical truth – which questions the reliability of the mathematical literature. He observes,
When I read a journal article, I often find mistakes,
and reasonably concludes that
The literature is unreliable.
For deep, difficult and long proofs, we can only “rely on the judgments of the bosses in the field”. And so,
…even in mathematics, truth can be political.
A first line of response might try to lessen the worry. A dangerous situation is one where a result which is used frequently in other results hangs itself from a single perilous thread. But fortunately there’s some useful feedback in the system. To the extent that the result is used frequently, people will look more closely at it to see if anything extra can be extracted, and in particular submit its proof to closer scrutiny. Alternative proofs are likely to follow. A result upon which little depends may well not receive this attention, but then its reliability matters less.
Smooth Differential Graded Algebra?
Posted by Urs Schreiber
A while ago I had a discussion with Todd Trimble about how to define “generalized smooth” differential graded-commutative algebras (DGCAs), generalizing the “generalized smooth”-algebras, called -algebras, discussed in the book by Moerdijk & Reyes. I think back then we fell short of arriving at a satisfactory conclusion.
As I mentioned, I would like to pick up that thread again and chat about some ideas.
This here is the general motivation:
given a category of “test objects”, generalized spaces are presheaves on , namely things that can be probed by throwing objects of into them, and generalized quantities (to be thought of as numbers, functions, sections, etc. as discussed in more detail below) are co-presheaves on .
If is the full subcategory of Manifolds on the manifolds , for all , then the spaces in question are something like “smooth spaces” (in particular, if their underlying presheaves happen to be concrete sheaves, these these are diffeological or Chen-smooth spaces) and then the quantities are something like “smooth quantities” (in particular, if the underlying co-presheaves happen to be monoidal, these are those -algebras).
Given such a notion of spaces, there is an obvious notion of higher spaces: pick your favorite definition of -groupoid. Then a higher degree space, an -space, should be an -groupoid internal to the above spaces.
What is the analog of this on the side of “quantities”? What is an -quantity? There are several possible answers one could come up with, I suppose, such as the answer by David Spivak, who replaces co-presheaves by simplicial co-presheaves and hence essentially follows the above -ization of spaces.
But here I am interested in a different kind of answer which supposes that -quantities corresponding to -spaces in the above sense are something like “quasi-free differential graded commutative -algebras” , qDGCAs – to be be determined.
There is a reason for this assumption, namely -Lie theory, but that is not of concern right now. Here I just want to talk about possible definitions of -qDGCAs, an interesting question in its own right.
September 7, 2008
Equivariant deRham Cohomology and Action Lie Algebroids
Posted by Urs Schreiber
The trimester program Geometry and Physics at the Hausdorff Institute in Bonnn is over. After a concentration of official activity around July it was getting a bit more relaxed again in August and we could pick up again our “internal seminar” among the program participants. Maybe a bit too relaxed: in the last weeks this internal seminar was attended just by Alejandro Cabrera and myself. But a 2-body seminar can be very useful.
I had mentioned a seminar talk by Alejandro on BV Poisson reduction recently here. Now in the internal seminar Alejandro was looking into the general mechanism of localization of integrals over graded spaces following
Richard Szabo
Equivariant Localization of Path Integrals
arXiv:hep-th/9608068
We talked about the relation of this to BV-BRST quantization. Maybe some of the things we discussed there are too top secret to be shared here for the moment, but I can share the following useful literature that Alejandro tracked down, on the relation between equivariant deRham cohomology and action Lie algebroids, and an interpretation of this in the context of rational approximations to universal -bundles in the sense of -connections (blog, arXiv).
8
Posted by John Baez
Next Saturday I’m going to the University of Glasgow to give talks about some of my favorite numbers: 5, 8 and 24. Different numbers have different personalities, as I try to explain here:
- Damien Henderson, Do numbers have personalities? You can count on it, The Herald, Sept. 6, 2008.
If you can’t attend, you can still pretend. So far I’m only satisfied with my talk on the number 8 — click on the title below to see the transparencies.
September 6, 2008
Military Research
Posted by John Baez
I just got an email from the U. C. Riverside grants office informing me of opportunities to apply for funding from the Multidisciplinary University Research Initiative. That sounds pretty bland… but the list of topics they’re funding is anything but! You see, this initiative is run by Office of Naval Research — a U.S. government agency that funds military research.
It’s interesting (and a bit creepy) to see what the U.S. military are excited about these days, so I thought I’d show you.
Will we see this stuff put to use in the next war?
Waldorf on Transport Functors and Connections on Gerbes
Posted by Urs Schreiber
Konrad Waldorf used to be a PhD student in Hamburg until recently and has now moved to Berkeley. Upon arrival there he has now given two talks on our joint work on parallel 2-transport. You can find nicely readable slides of his talks on his website
Konrad Waldorf
Connections on non-abelian gerbes and their holonomy
(pdf slides part I, part II)
September 3, 2008
Comparative Smootheology, III
Posted by John Baez
Recently on the category theory mailing list, Bill Lawvere mentioned Chen’s work on smooth spaces. Jim Stasheff suggest that he post his remarks to our thread on comparative smootheology. I mentioned my recent paper with Alex Hoffnung where we showed that the category of Chen spaces is a ‘quasitopos’. Chen spaces are sets equipped with a collection of ‘plots’, a severe generalization of the ‘charts’ familiar from smooth manifolds. A ‘quasitopos’ is a nice sort of category that’s almost, but not quite a topos.
Lawvere replied saying that it’s a step backwards to treat smooth spaces as sets with extra structure. After all, his work together with Anders Kock and others gets an actual topos of smooth spaces — including ‘infinitesimal’ spaces that allow a beautiful approach to calculus with infinitesimals! — precisely by dropping the requirement that smooth spaces be sets with extra structure.
Jim Stasheff suggested that I post my reply to the -Category Café. Since that reply makes little sense without the whole exchange, I’ll post the whole thing. There’s a certain amount of heat in Lawvere’s comments — but never mind: let’s focus on the math.
To understand Lawvere’s work on smooth spaces, I suggest starting here:
- F. William Lawvere, Toward the description in a smooth topos of the dynamically possible motions and deformations of a continuous body.
- F. William Lawvere, Toposes of laws of motion.
For a full-fledged textbook treatment, which may be gentler for beginners, try this:
- Anders Kock, Synthetic Differential Geometry.
 Posts with this logo use
Posts with this logo use 














