Lie Theory Through Examples 1

September 30, 2008

Posted by John Baez

$MathML-enabled post (click for more details).$

Simple Lie groups and Lie algebras tie together some of the most beautiful, symmetrical structures in mathematics: Platonic solids and their higher-dimensional cousins, finite groups generated by reflections, lattice packings of spheres, incidence geometries, symmetric spaces, and more. In this fall’s seminar we’ll explore this web of ideas through examples, starting with easy ‘classical’ ones and working up to ‘exceptional’ ones such as the 248-dimensional Lie group $E_8$ .

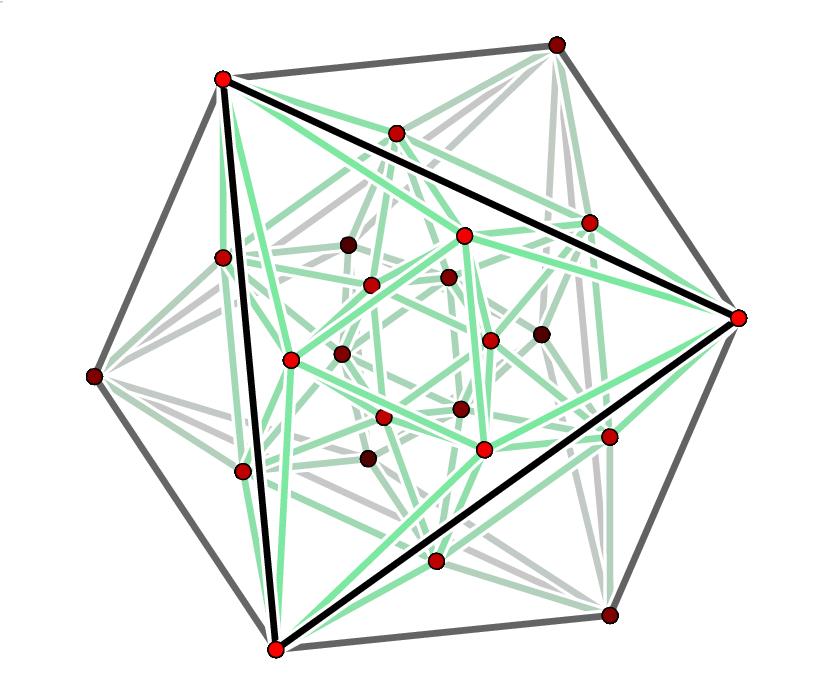
(Here are the 24 roots of $D_4$ , projected from 4 dimensions down to 3, and then drawn on the plane.)

$MathML-enabled post (click for more details).$

I’m not sure I’ll have the energy to prepare course notes for this class in LaTeX — but I think it’s worth a try, since I’ve long been wanting to write a book on this subject, and this would be a good way to start. So:

Lecture 1 — Introduction. The simplest interesting example: $A_2$ .

The $A_2$ lattice is a pretty simple thing: it yields the densest way to pack pennies on the plane. We can also think of it as the “Eisenstein integers” — the complex numbers of the form $a + b \omega$ where $a,b$ are integers and $\omega$ is a cube root of 1:

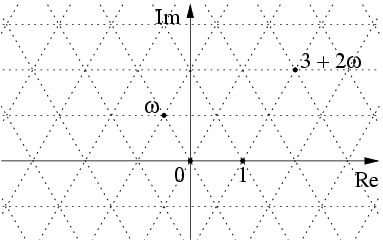
They’re closed under addition and multiplication. In fact, they’re the algebraic integers in the number field $\mathbb{Q}[\omega]$ . But I’m going to focus on how $A_2$ shows up naturally when you think about the group $SU(3)$ .

Posted at September 30, 2008 1:20 AM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1804

24 Comments & 0 Trackbacks

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

Typo on p.5, start of paragraph 4: the kernel of $exp$ is a subgroup of \mathfrak{t}, not of $T$ .

Thanks for sharing the lovely notes!

Posted by: Peter on September 30, 2008 2:29 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Thanks!

The notes are sort of rambling and conversational; I’d like someday to write a book that keeps a bit of that tone, but fixes some of the problems with what I’ve written so far.

In particular, it may terrify some people to see such a heavy list of things that Dynkin diagrams classify, before seeing any examples.

On the other hand, other people will be unhappy to plow through examples before knowing what they’re examples of.

It’s a chicken-and-egg problem. Maybe I should say something like “This list may seem scary now, but don’t worry — come back to it later, and it’ll make more sense.”

Posted by: John Baez on September 30, 2008 4:59 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Reminds me of the advice of the anonymous author of `The Cloud of Unknowing’.

For peradventure there is some matter therein in the beginning or in the middle, the which is hanging, and not fully declared where it standeth: and if it be not there, it is soon after, or else in the end.

Posted by: jim stasheff on October 1, 2008 2:02 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

No wonder it’s called the ‘Cloud of Unknowing’ — I can’t make heads or tails of that sentence, though I admit it sounds great.

Posted by: John Baez on October 3, 2008 4:52 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Translation: It may be there is some matter in this book in the beginning or in the middle that is incomplete or not fully exposed where it first occurs, but if not, it will be soon thereafter or else at the end (of the book).

Paraphrase: If something is unclear, don’t give up but persevere and it may become clear later.

Posted by: jim stasheff on October 4, 2008 1:30 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

No wonder it’s called the ‘Cloud of Unknowing’

I won’t say there’s an elephant in the room, but I think it’s true that the author of this utterance needs no introduction to the illustrious readers of this blog:

To study spaces which admit $A_n$ -structures, we can work directly with the maps…. In the case of a topological group, this amounts to working only with the classifying bundle and never mentioning group operations. This would be an exercise in rectitude of thought of which it would be pointless to countenance the austerity, for not only would it eliminate a useful perspective on the subject, but, by disguising its own main point, it would place the reader behind a cloud of unknowing.

I love that sentence – one of the most awesome and magisterial I’ve seen anywhere in the mathematical literature.

Posted by: Todd Trimble on October 4, 2008 4:15 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

I hope you youngun’s will recognize the implied put down of a treatise by the famous X and Y.

Posted by: jim stasheff on October 4, 2008 10:31 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

Todd, in my copy I don’t have the same preposition:

…it would place the reader beneath a cloud of unknowing.

This leads me to a different mental image – I see a sodden walker on a hill.

Posted by: Simon Willerton on October 4, 2008 10:50 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

I thought something sounded off about that! I should have checked the original copy, but I was lazy and transcribed it off of this tribute (page 10). I like “beneath” better myself.

Posted by: Todd Trimble on October 5, 2008 1:32 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Yes I am going to enjoy this course too. For some weird reason I think I found the old handwritten notes style more pretty than this new LaTex style but it’s no doubt just a misplaced form of nostalgia.

Posted by: Bruce Bartlett on October 1, 2008 12:35 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Derek Wise took wonderful notes, with a great sense of graphic design. He also included lots of stuff I said but didn’t write on the blackboard. I’ve never found his equal since, though Alex Hoffnung manfully stepped forward to fill the gap.

Since I want to write a book about symmetry someday, I thought I should try composing my notes in LaTeX and get a head start. We’ll see how it goes. I hope that by teaching the class just once a week instead of twice, I’ll be able to keep up.

Posted by: John Baez on October 3, 2008 4:50 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

If anyone wants handwritten notes to go along with the LaTeX version that John has created just let me know and I would be happy to pass them along.

Posted by: Alex Hoffnung on October 8, 2008 3:55 AM | Permalink | Reply to this

Root polytopes; Re: Lie Theory Through Examples 1

New for 1 Oct 2008:

Root polytopes and growth series of root lattices

arXiv:0809.5123
Title: Root polytopes and growth series of root lattices
Authors: Federico Ardila, Matthias Beck, Serkan Hosten, Julian Pfeifle, Kim Seashore
Comments: 17 pages, 3 figures
Subjects: Combinatorics (math.CO); Commutative Algebra (math.AC)

The convex hull of the roots of a classical root lattice is called a root polytope. We determine explicit unimodular triangulations of the boundaries of the root polytopes associated to the root lattices A_n, C_n, and D_n, and compute their f-and h-vectors. This leads us to recover formulae for the growth series of these root lattices, which were first conjectured by Conway-Mallows-Sloane and Baake-Grimm and proved by Conway-Sloane and Bacher-de la Harpe-Venkov.

Posted by: Jonathan Vos Post on October 1, 2008 2:51 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

This is too good to be true!

Thanks so much for these lectures.

Posted by: Christian on October 1, 2008 11:21 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

I hope it’s not too good to be true. It’s with some trepidation that I begin what might become a book I’ve been wanting to write all my life… maybe because writing books is hellishly difficult, or maybe because once I’ve done most of I’ve wanted to do all my life, it must mean my life is more than half over. But I’ll just see how it goes.

For years I’ve been dreaming about writing two books called Classical Beauty and Exotic Beauty. They’d be about the ‘classical’ and ‘exceptional’ groups, and the structures that have these groups as symmetries. The ‘classical’ book would be about constructions that work uniformly in infinitely many cases, while the ‘exotic’ book would be about constructions that work only because of amazing ‘coincidences’.

(Maybe the second book should be called ‘exceptional beauty’, but I think ‘exotic beauty’ sounds more alluring, less like a math book.)

Posted by: John Baez on October 8, 2008 5:21 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Euclid alone has looked on beauty bare. But Baez has looked at exotic beauty in naked splendor. To see what he saw, enter your credit card number here…

Posted by: Jonathan Vos Post on October 9, 2008 5:23 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

What happend to this course? Is it coming back someday?

Posted by: Christian on November 25, 2008 4:46 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

The actual course is going on quite nicely, but I’ve been very busy, so I’ve been discarding all inessential activities: I’ve given more lectures than I’ve written up, and I’ve written up more lectures than I’ve blogged.

Have you read all the ones I’ve written up? If so, you’ll have to wait a week or two — the quarter is almost over, and next quarter will be less busy for me, so I’ll start catching up. Right now I’m giving lectures about the Spin groups.

Posted by: John Baez on November 25, 2008 8:58 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

writing up your lectures? I thought that was a job for grad student(s)

i’m sure glad I did Milnor’s

Posted by: jim stasheff on November 25, 2008 10:40 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

Sadly, it turns out to be less work to write lecture notes myself than to polish the notes written by a grad student until I’m happy with them.

If I were a Milnor, I might have a Stasheff for a grad student, and maybe things would work more smoothly.

Posted by: John Baez on November 26, 2008 6:02 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

Ah, I understand. I can wait! Great to know that more lectures will come, I was a bit worried..

Posted by: Christian on November 25, 2008 9:32 PM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

There are some new notes out on exceptional Lie groups, by a Japanese guy named Ichiro Yokota. Maybe someone here is interested in those.

http://arxiv.org/abs/0902.0431

Posted by: Christian on March 25, 2009 7:35 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

$MathML-enabled post (click for more details).$

Thanks, I’ll read these notes! I’m exceptionally interested in these Lie groups. I plan to talk about them next quarter in the seminar.

The last sentence in Yokota’s abstract is amusing and slightly wistful.

I have more notes for my Lie Theory Through Examples seminar, but they’re hand-written, and I haven’t put them on my website yet. I’ve been too busy to write stuff in TeX.

Posted by: John Baez on March 25, 2009 7:47 AM | Permalink | Reply to this

Re: Lie Theory Through Examples 1

“At any rate, we would like this book to be used in mathematics and physics. “

I view this as honest, motivational, and positive about breaking down the cultural barriers between the fields, as you so often do.

Posted by: Jonathan Vos Post on March 25, 2009 6:12 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

September 30, 2008