August 28, 2016
Topological Crystals (Part 4)
Posted by John Baez
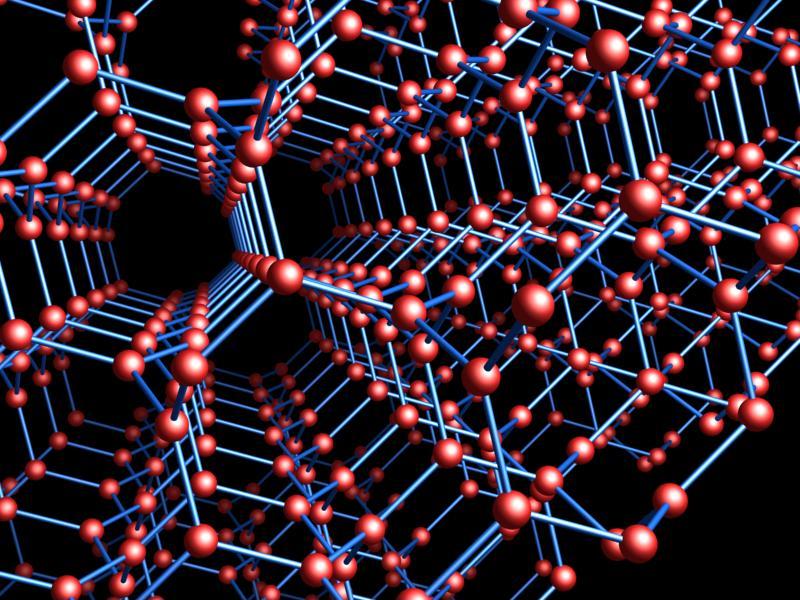
Okay, let’s look at some examples of topological crystals. These are what got me excited in the first place. We’ll get some highly symmetrical crystals, often in higher-dimensional Euclidean spaces. The ‘triamond’, above, is a 3d example.
August 27, 2016
Jobs at Heriot-Watt
Posted by Tom Leinster
We at the mathematics department at the University of Edinburgh are doing more and more things in conjunction with our sisters and brothers at Heriot–Watt University, also in Edinburgh. For instance, our graduate students take classes together, and about a dozen of them are members of both departments simultaneously. We’re planning to strengthen those links in the years to come.
The news is that Heriot–Watt are hiring.
August 25, 2016
Monoidal Categories with Projections
Posted by Tom Leinster
Monoidal categories are often introduced as an abstraction of categories with products. Instead of having the categorical product , we have some other product , and it’s required to behave in a somewhat product-like way.
But you could try to abstract more of the structure of a category with products than monoidal categories do. After all, when a category has products, it also comes with special maps and for every and (the projections). Abstracting this leads to the notion of “monoidal category with projections”.
I’m writing this because over at this thread on magnitude homology, we’re making heavy use of semicartesian monoidal categories. These are simply monoidal categories whose unit object is terminal. But the word “semicartesian” is repellently technical, and you’d be forgiven for believing that any mathematics using “semicartesian” anythings is bound to be going about things the wrong way. Name aside, you might simply think it’s rather ad hoc; the nLab article says it initially sounds like centipede mathematics.
I don’t know whether semicartesian monoidal categories are truly necessary to the development of magnitude homology. But I do know that they’re a more reasonable and less ad hoc concept than they might seem, because:
Theorem A semicartesian monoidal category is the same thing as a monoidal category with projections.
So if you believe that “monoidal category with projections” is a reasonable or natural concept, you’re forced to believe the same about semicartesian monoidal categories.
August 19, 2016
Compact Closed Bicategories
Posted by John Baez
I’m happy to announce that this paper has been published:
- Mike Stay, Compact closed bicategories, Theory and Applications of Categories 31 (2016), 755–798.
Abstract. A compact closed bicategory is a symmetric monoidal bicategory where every object is equipped with a weak dual. The unit and counit satisfy the usual ‘zig-zag’ identities of a compact closed category only up to natural isomorphism, and the isomorphism is subject to a coherence law. We give several examples of compact closed bicategories, then review previous work. In particular, Day and Street defined compact closed bicategories indirectly via Gray monoids and then appealed to a coherence theorem to extend the concept to bicategories; we restate the definition directly.
We prove that given a 2-category with finite products and weak pullbacks, the bicategory of objects of , spans, and isomorphism classes of maps of spans is compact closed. As corollaries, the bicategory of spans of sets and certain bicategories of ‘resistor networks” are compact closed.
August 11, 2016
A Survey of Magnitude
Posted by Tom Leinster
The notion of the magnitude of a metric space was born on this blog. It’s a real-valued invariant of metric spaces, and it came about as a special case of a general definition of the magnitude of an enriched category (using Lawvere’s amazing observation that metric spaces are usefully viewed as a certain kind of enriched category).
Anyone who’s been reading this blog for a while has witnessed the growing-up of magnitude, with all the attendant questions, confusions, misconceptions and mess. (There’s an incomplete list of past posts here.) Parents of grown-up children are apt to forget that their offspring are no longer helpless kids, when in fact they have a mortgage and children of their own. In the same way, it would be easy for long-time readers to have the impression that the theory of magnitude is still at the stage of resolving the basic questions.
Certainly there’s still a great deal we don’t know. But by now there’s also lots we do know, so Mark Meckes and I recently wrote a survey paper:
Tom Leinster and Mark Meckes, The magnitude of a metric space: from category theory to geometric measure theory. ArXiv:1606.00095; also to appear in Nicola Gigli (ed.), Measure Theory in Non-Smooth Spaces, de Gruyter Open.
Here I’ll tell you some of the highlights: ten things we used not to know, but do now.
August 10, 2016
Two Miracles of Algebraic Geometry
Posted by John Baez
In real analysis you get just what you pay for. If you want a function to be seven times differentiable you have to say so, and there’s no reason to think it’ll be eight times differentiable.
But in complex analysis, a function that’s differentiable is infinitely differentiable, and its Taylor series converges, at least locally. Often this lets you extrapolate the value of a function at some faraway location from its value in a tiny region! For example, if you know its value on some circle, you can figure out its value inside. It’s like a fantasy world.
Algebraic geometry has similar miraculous properties. I recently learned about two.
August 9, 2016
In Praise of the Gershgorin Disc Theorem
Posted by Tom Leinster
I’m revising the notes for the introductory linear algebra class that I teach, and wondering whether I can find a way to fit in the wonderful but curiously unpromoted Gershgorin disc theorem.
The Gershgorin disc theorem is an elementary result that allows you to make very fast deductions about the locations of eigenvalues. For instance, it lets you look at the matrix
and see, with only the most trivial mental arithmetic, that the real parts of its eigenvalues must all lie between and and the imaginary parts must lie between and .
I wasn’t taught this theorem as an undergraduate, and ever since I learned it a few years ago, have wondered why not. I feel ever so slightly resentful about it. The theorem is so useful, and the proof is a pushover. Was it just me? Did you get taught the Gershgorin disc theorem as an undergraduate?
August 8, 2016
What is a Formal Proof?
Posted by Mike Shulman
There’s been some discussion recently in the homotopy type theory community about questions like “must type-checking always be decidable?” While the specific phrasing of this question is specific to type theory (and somewhat technical as well), it is really a manifestation of a deeper and more general question: what is a formal proof?
At one level, the answer to this question is a matter of definition: any particular foundational system for mathematics defines what it considers to be a “formal proof”. However, the current discussions are motivated by questions in the design of foundational systems, so this is not the relevant answer. Instead the question is what properties should a notion of “formal proof” satisfy for it to be worthy of the name?
August 6, 2016
Topological Crystals (Part 3)
Posted by John Baez
Last time I explained how to build the ‘maximal abelian cover’ of a connected graph. Now I’ll say more about a systematic procedure for embedding this into a vector space. That will give us a topological crystal, like this:
Some remarkably symmetrical patterns arise this way!
 Posts with this logo use
Posts with this logo use