Topological Crystals (Part 3)
Posted by John Baez
Last time I explained how to build the ‘maximal abelian cover’ of a connected graph. Now I’ll say more about a systematic procedure for embedding this into a vector space. That will give us a topological crystal, like this:
Some remarkably symmetrical patterns arise this way!
For example, starting from this graph:

we get this:
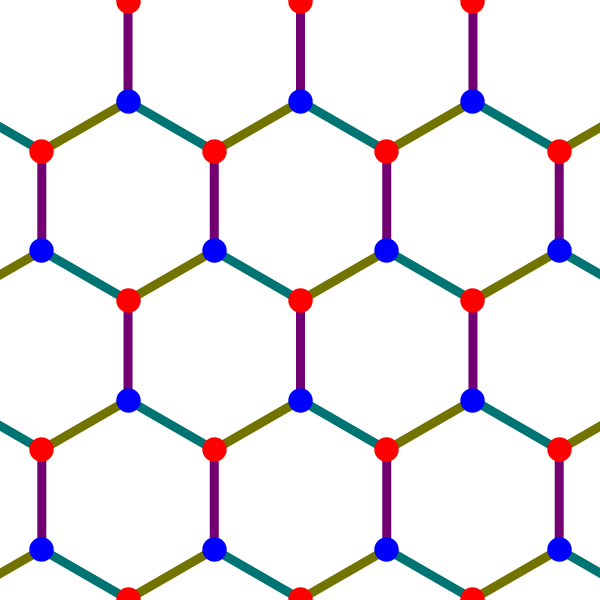
Nature uses this pattern for crystals of graphene.
Starting from this graph:

we get this:
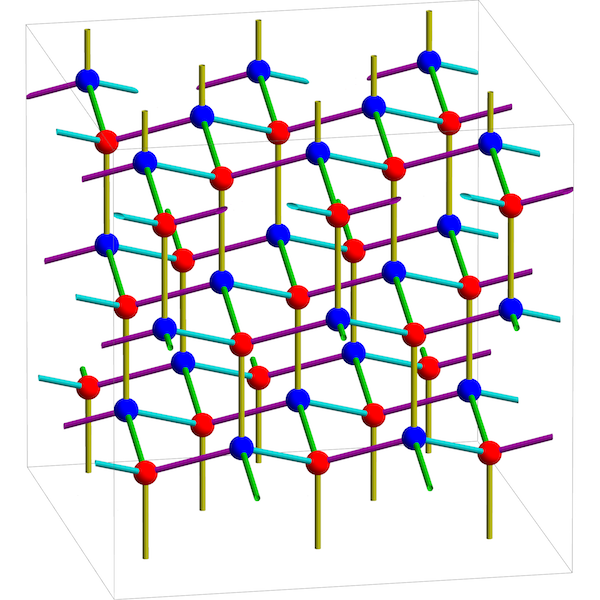
Nature uses this for crystals of diamond! Since the construction depends only on the topology of the graph we start with, we call this embedded copy of its maximal abelian cover a topological crystal.
Today I’ll remind you how this construction works. I’ll also outline a proof that it gives an embedding of the maximal abelian cover if and only if the graph has no bridges: that is, edges that disconnect the graph when removed. I’ll skip all the hard steps of the proof, but they can all be found here:
- John Baez, Topological crystals.
The homology of graphs
I’ll start with some standard stuff that’s good to know. Let be a graph. Remember from last time that we’re working in a setup where every edge goes from a vertex called its source to a vertex called its target . We write to indicate that is going from to . You can think of the edge as having an arrow on it, and if you turn the arrow around you get the inverse edge, . Also, .
The group of integral 0-chains on , , is the free abelian group on the set of vertices of . The group of integral 1-chains on , , is the quotient of the free abelian group on the set of edges of by relations for every edge . The boundary map is the homomorphism
such that
for each edge , and
is the group of integral 1-cycles on .
Remember, a path in a graph is a sequence of edges, the target of each one being the source of the next. Any path in determines an integral 1-chain:
For any path we have
and if and are composable then
Last time I explained what it means for two paths to be ‘homologous’. Here’s the quick way to say it. There’s groupoid called the fundamental groupoid of , where the objects are the vertices of and the morphisms are freely generated by the edges except for relations saying that the inverse of really is . We can abelianize the fundamental groupoid by imposing relations saying that whenever this equation makes sense. Each path gives a morphism which I’ll call in the abelianized fundamental groupoid. We say two paths are homologous if .
Here’s a nice thing:
Lemma A. Let be a graph. Two paths in are homologous if and only if they give the same 1-chain: .
Proof. See the paper. You could say they give ‘homologous’ 1-chains, too, but for graphs that’s the same as being equal. █
We define vector spaces of 0-chains and 1-chains by
respectively. We extend the boundary map to a linear map
We let be the kernel of this linear map, or equivalently,
and we call elements of this vector space 1-cycles. Since is a free abelian group, it forms a lattice in the space of 1-cycles. Any edge of can be seen as a 1-chain, and there is a unique inner product on such that edges form an orthonormal basis (with each edge counting as the negative of .) There is thus an orthogonal projection
This is the key to building topological crystals!
The embedding of atoms
We now come to the main construction, first introduced by Kotani and Sunada. To build a topological crystal, we start with a connected graph with a chosen basepoint . We define an atom to be a homology class of paths starting at the basepoint, like
Last time I showed that these atoms are the vertices of the maximal abelian cover of . Now let’s embed these atoms in a vector space!
Definition. Let be a connected graph with a chosen basepoint. Let be its set of atoms. Define the map
by
That is well-defined follows from Lemma A. The interesting part is this:
Theorem A. The following are equivalent:
- The graph has no bridges.
- The map is one-to-one.
Proof. The map is one-to-one if and only if for any atoms and , implies . Note that is a path in with , so
Since vanishes if and only if is orthogonal to every 1-cycle, we have
On the other hand, Lemma A says
Thus, to prove (1)(2), it suffices to that show that has no bridges if and only if every 1-chain orthogonal to every 1-cycle has . This is Lemma D below. █
The following lemmas are the key to the theorem above — and also a deeper one saying that if has no bridges, we can extend to an embedding of the whole maximal abelian cover of .
For now, we just need to show that any nonzero 1-chain coming from a path in a bridgeless graph has nonzero inner product with some 1-cycle. The following lemmas, inspired by an idea of Ilya Bogdanov, yield an algorithm for actually constructing such a 1-cycle. This 1-cycle also has other desirable properties, which will come in handy later.
To state these, let a simple path be one in which each vertex appears at most once. Let a simple loop be a loop in which each vertex except appears at most once, while appears exactly twice, as the starting point and ending point. Let the support of a 1-chain , denoted , be the set of edges such that . This excludes edges with , but also those with , which are inverses of edges in the support. Note that
So, is the smallest set of edges such that can be written as a positive linear combination of edges in this set.
Okay, here are the lemmas!
Lemma B. Let be any graph and let be an integral 1-cycle on . Then for some we can write
where are simple loops with .
Proof. See the paper. The proof is an algorithm that builds a simple loop with . We subtract this from , and if the result isn’t zero we repeat the algorithm, continuing to subtract off 1-cycles until there’s nothing left. █
Lemma C. Let be a path in a graph . Then for some we can write
where is a simple path and are simple loops with .
Proof. This relies on the previous lemma, and the proof is similar — but when we can’t subtract off any more ’s we show what’s left is for a simple path . █
Lemma D. Let be a graph. Then the following are equivalent:
- has no bridges.
- For any path in , if is orthogonal to every 1-cycle then .
Proof. It’s easy to show a bridge gives a nonzero 1-chain that’s orthogonal to all 1-cycles, so the hard part is showing that for a bridgeless graph, if is orthogonal to every 1-cycle then . The idea is to start with a path for which . We hit this path with Lemma C, which lets us replace by a simple path . The point is that a simple path is a lot easier to deal with than a general path: a general path could wind around crazily, passing over every edge of our graph multiple times.
Then, assuming has no bridges, we use Ilya Bogdanov’s idea to build a 1-cycle that’s not orthogonal to . The basic idea is to take the path and write it out as . Since the last edge is not a bridge, there must be a path from back to that does not use the edge or its inverse. Combining this path with we can construct a loop which gives a cycle having nonzero inner product with and thus with .
I’m deliberately glossing over some difficulties that can arise, so see the paper for details! █
Embedding the whole crystal
Okay: so far, we’ve taken a connected bridgeless graph and embedded its atoms into the space of 1-cycles via a map
These atoms are the vertices of the maximal abelian cover . Now we’ll extend to an embedding of the whole graph — or to be precise, its geometric realization . Remember, for us a graph is an abstract combinatorial gadget; its geometric realization is a topological space where the edges become closed intervals.
The idea is that just as maps each atom to a point in the vector space , maps each edge of to a straight line segment between such points. These line segments serve as the ‘bonds’ of a topological crystal. The only challenge is to show that these bonds do not cross each other.
Theorem B. If is a connected graph with basepoint, the map extends to a continuous map
sending each edge of to a straight line segment in . If has no bridges, then is one-to-one.
Proof. The first part is easy; the second part takes real work! The problem is to show the edges don’t cross. Greg Egan and I couldn’t do it using just Lemma D above. However, there’s a nice argument that goes back and uses Lemma C — read the paper for details.
As usual, history is different than what you read in math papers: David Speyer gave us a nice proof of Lemma D, and that was good enough to prove that atoms are mapped into the space of 1-cycles in a one-to-one way, but we only came up with Lemma C after weeks of struggling to prove the edges don’t cross. █
Connections to tropical geometry
Tropical geometry sets up a nice analogy between Riemann surfaces and graphs. The Abel–Jacobi map embeds any Riemann surface in its Jacobian, which is the torus . We can similarly define the Jacobian of a graph to be . Theorem B yields a way to embed a graph, or more precisely its geometric realization , into its Jacobian. This is the analogue, for graphs, of the Abel–Jacobi map.
After I put this paper on the arXiv, I got an email from Matt Baker saying that he had already proved Theorem A — or to be precise, something that’s clearly equivalent. It’s Theorem 1.8 here:
- Matthew Baker and Serguei Norine, Riemann–Roch and Abel–Jacobi theory on a finite graph.
This says that the vertices of a bridgeless graph are embedded in its Jacobian by means of the graph-theoretic analogue of the Abel–Jacobi map.
What I really want to know is whether someone’s written up a proof that this map embeds the whole graph, not just its vertices, into its Jacobian in a one-to-one way. That would imply Theorem B. For more on this, try my conversation with David Speyer.
Anyway, there’s a nice connection between topological crystallography and tropical geometry, and not enough communication between the two communities. Once I figure out what the tropical folks have proved, I will revise my paper to take that into account.
Next time I’ll talk about more examples of topological crystals!

Re: Topological Crystals (Part 3)
This looks like fun stuff! The remarks about the Laves graph on p.2 of the paper are especially cool. It also seems vaguely related to a paper that I wrote a couple of years ago with a general rigorous version of Weyl’s tile argument against the idea that space may be discrete.
One starts with a periodic graph as a mathematical model for discrete space. One then writes it as a cover of a finite graph with a free abelian group of deck transformations. The difference to topological crystals here is that the “base” graph comes equipped with edge weights in which assign to every edge the number of unit cells that one has to translate in the covering space. The one can recover the original periodic graph via the Grothendieck construction. The edge weights also span the unit ball of a norm on homology which governs the large-scale geometry of the graph, and this is how the discreteness of space could become manifest macroscopically. The green hexagon in your figure from Part 1 may be a scaled-up version of this unit ball:
Unfortunately, I learned of the closely related work of Kotani and Sunada only after the paper had appeared. They have more results and the better abstract perspective!