Topological Crystals (Part 1)
Posted by John Baez
Over on Azimuth I posted an article about crystals:
- John Baez, Diamonds and triamonds, Azimuth, 11 April 2016.
In the comments on that post, a bunch of us worked on some puzzles connected to ‘topological crystallography’—a subject that blends graph theory, topology and mathematical crystallography. You can learn more about that subject here:
- Tosio Sunada, Crystals that nature might miss creating, Notices of the AMS 55 (2008), 208–215.
I got so interested that I wrote this paper about it, with massive help from Greg Egan:
- John Baez, Topological crystals.
I’ll explain the basic ideas in a series of posts here.
First, a few personal words.
I feel a bit guilty putting so much work into this paper when I should be developing network theory to the point where it does our planet some good. I seem to need a certain amount of beautiful pure math to stay sane. But this project did at least teach me a lot about the topology of graphs.
For those not in the know, applying homology theory to graphs might sound fancy and interesting. For people who have studied a reasonable amount of topology, it probably sounds easy and boring. The first homology of a graph of genus is a free abelian group on generators: it’s a complete invariant of connected graphs up to homotopy equivalence. Case closed!
But there’s actually more to it, because studying graphs up to homotopy equivalence kills most of the fun. When we’re studying networks in real life we need a more refined outlook on graphs. So some aspects of this project might pay off, someday, in ways that have nothing to do with crystallography. But right now I’ll just talk about it as a fun self-contained set of puzzles.
I’ll start by quickly sketching how to construct topological crystals, and illustrate it with the example of graphene, a 2-dimensional form of carbon:

I’ll precisely state our biggest result, which says when the construction gives a crystal where the atoms don’t bump into each other and the bonds between atoms don’t cross each other. Later I may come back and add detail, but for now you can find details in our paper.
Constructing topological crystals
The ‘maximal abelian cover’ of a graph plays a key role in Sunada’s work on topological crystallography. Just as the universal cover of a connected graph has the fundamental group as its group of deck transformations, the maximal abelian cover, denoted , has the abelianization of as its group of deck transformations. It thus covers every other connected cover of whose group of deck transformations is abelian. Since the abelianization of is the first homology group , there is a close connection between the maximal abelian cover and homology theory.
In our paper, Greg and I prove that for a large class of graphs, the maximal abelian cover can naturally be embedded in the vector space . We call this embedded copy of a ‘topological crystal’. The symmetries of the original graph can be lifted to symmetries of its topological crystal, but the topological crystal also has an -dimensional lattice of translational symmetries. In 2- and 3-dimensional examples, the topological crystal can serve as the blueprint for an actual crystal, with atoms at the vertices and bonds along the edges.
The general construction of topological crystals was developed by Kotani and Sunada, and later by Eon. Sunada uses ‘topological crystal’ for an even more general concept, but we only need a special case.
Here’s how it works. We start with a graph . This has a space of 0-chains, which are formal linear combinations of vertices, and a space of 1-chains, which are formal linear combinations of edges. There is a boundary operator
This is the linear operator sending any edge to the difference of its two endpoints. The kernel of this operator is called the space of 1-cycles, . There is an inner product on the space of 1-chains such that edges form an orthonormal basis. This determines an orthogonal projection
For a graph, is isomorphic to the first homology group . So, to obtain the topological crystal of , we need only embed its maximal abelian cover in . We do this by embedding in and then projecting it down via .
To accomplish this, we need to fix a basepoint for . Each path in starting at this basepoint determines a 1-chain . These 1-chains correspond to the vertices of . The graph has an edge from to whenever the path is obtained by adding an extra edge to . This edge is a straight line segment from the point to the point .
The hard part is checking that the projection maps this copy of into in a one-to-one manner. In Theorems 6 and 7 of our paper we prove that this happens precisely when the graph has no ‘bridges’: that is, edges whose removal would disconnect .
Kotani and Sunada noted that this condition is necessary. That’s actually pretty easy to see. The challenge was to show that it’s sufficient! For this, our main technical tool is Lemma 5, which for any path decomposes the 1-chain into manageable pieces.
We call the resulting copy of embedded in a topological crystal.
Let’s see how it works in an example!
Take to be this graph:

Since has 3 edges, the space of 1-chains is 3-dimensional. Since has 2 holes, the space of 1-cycles is a 2-dimensional plane in this 3-dimensional space. If we take paths in starting at the red vertex, form the 1-chains , and project them down to this plane, we obtain the following picture:
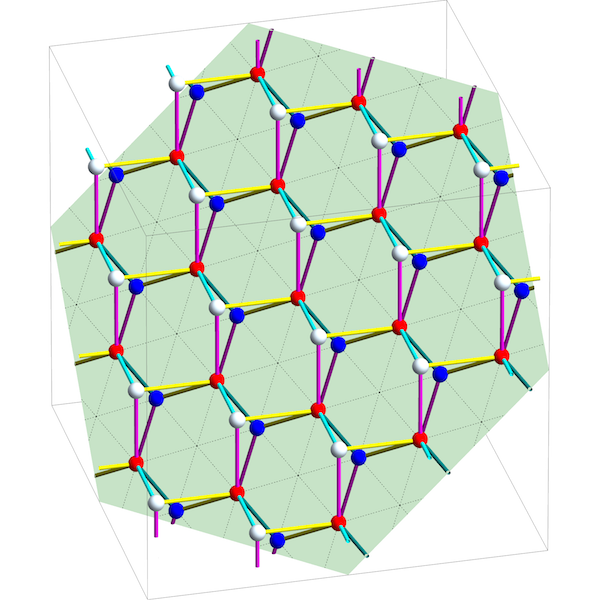
Here the 1-chains are the white and red dots. These are the vertices of , while the line segments between them are the edges of . Projecting these vertices and edges onto the plane of 1-cycles, we obtain the topological crystal for . The blue dots come from projecting the white dots onto the plane of 1-cycles, while the red dots already lie on this plane. The resulting topological crystal provides the pattern for graphene:
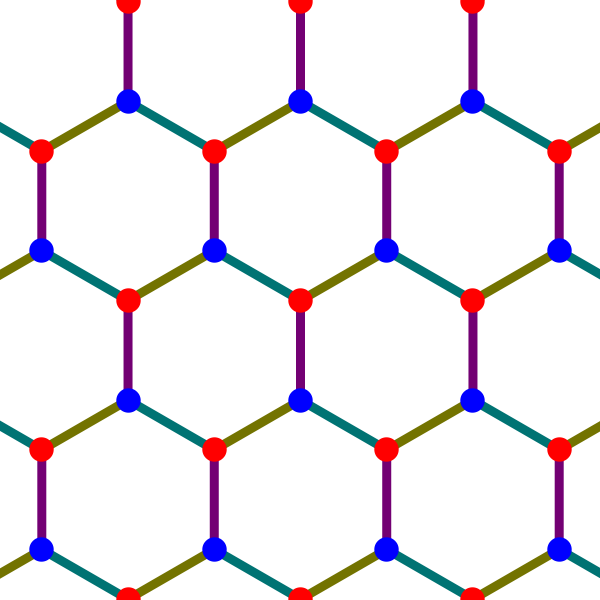
That’s all there is to the basic idea! But there’s a lot more to say about the mathematics it leads to, and a lot of fun examples to look at: diamonds, triamonds, hyperquartz and more.

Re: Topological Crystals (Part 1)
In email, Timothy Porter said this post reminded me of some stuff from a workshop in Bangor back in 2000, on Orbifolds and Crystallography. They invited Haefliger and also Carroll Johnson from Oak Ridge National Laborator, who has a website on this material:
The extended abstract for his Bangor talk is here.
My work with Egan is not directly related to orbifolds. From what I gather, the relevance of orbifolds is that you can take 3-dimensional space and mod out by the symmetry group of a crystal and get an orbifold. Of course you could just get a topological space, but orbifolds allow you to keep clear track of which points are fixed by more symmetries than the average point.
This works for any crystal. What Egan and I are doing is different. Following an idea of Sunada, we’re starting from any finite graph with no bridges—no edges whose removal disconnects the graph— and using this to build a crystal in , where is the genus of the graph. This crystal is itself a graph, with ‘atoms’ as vertices and ‘bonds’ as edges. And this graph is the maximal abelian cover of .
Proving that we really get a copy of the maximal abelian cover embedded in turns out to require some work. I’ll try to sketch how that goes.
And then there are various fun things you can do, like try to figure out various properties of this crystal depend on the original graph .